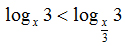Đề thi thử Đại học năm 2013 - môn Toán (Đề 29)
ĐỀ THI THỬ ĐẠI HỌC - CAO ĐẲNG
NĂM 2012 - 2013
MÔN THI: TOÁN
Đề số 29
PHẦN CHUNG CHO TẤT CẢ CÁC THÍ SINH (7 điểm)
Câu I. (2 điểm)
Cho hàm số y = x3 + mx + 2 (1)
1. Khảo sát sự biến thiên và vẽ đồ thị của hàm số (1) khi m = -3.
2. Tìm m để đồ thị hàm số (1) cắt trục hòanh tại một điểm duy nhất.
Câu II. (2 điểm)
1. Giải hệ phương trình: 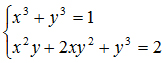
2. Giải phương trình: 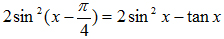
Câu III. (1 điểm) Tính tích phân:
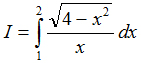
Câu IV. (1 điểm)
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA = h vuông góc mặt phẳng (ABCD), M là điểm thay đổi trên CD. Kẻ SH vuông góc BM. Xác định vị trí M để thể tích tứ diện S.ABH đạt giá trị lớn nhất. Tính giá trị lớn nhất đó.
Câu V. (1 điểm) Tìm m để phương trình sau có nghiệm thực: 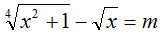
II. PHẦN RIÊNG. (3 điểm)
Thí sinh chỉ được làm một trong hai phần (phần a họăc phần b)
Câu VI a. (2 điểm)
1. Trong hệ tọa độ Oxy, cho hai đường thẳng d1: x – 2y + 3 = 0, d2: 4x + 3y – 5 = 0. Lập phương trình đường tròn (C) có tâm I trên d1, tiếp xúc d2 và có bán kính R = 2.
2. Cho hai đường thẳng 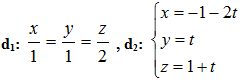 và mặt phẳng (P): x – y – z = 0. Tìm tọa độ hai điểm M thuộc d1, N thuộc d2 sao cho MN song song (P) và MN =
và mặt phẳng (P): x – y – z = 0. Tìm tọa độ hai điểm M thuộc d1, N thuộc d2 sao cho MN song song (P) và MN = 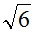
Câu VII a. (1 điểm) Tìm số phức z thỏa mãn: 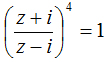
Câu VI b. (2 điểm)
1. Cho hình chữ nhật ABCD có cạnh AB: x – 2y – 1 = 0, đường chéo BD: x – 7y + 14 = 0 và đường chéo AC qua điểm M(2 ; 1). Tìm tọa độ các đỉnh của hình chữ nhật.
2. Cho ba điểm O(0; 0; 0), A(0; 0; 4), B(2; 0; 0) và mặt phẳng (P): 2x + 2y – z + 5 = 0. Lập phương trình mặt cầu (S) đi qua ba điểm O, A, B và có khoảng cách từ tâm I đến mặt phẳng (P) bằng 5/3
Câu VII b. (1điểm) Giải bất phương trình: