Đề thi tuyển sinh lớp 10 THPT năm học 2013 môn Toán - Lào Cai
Để chuẩn bị cho kỳ thi vào cấp 3 sắp tới, Vndoc.com xin gửi đến các bạn: Đề thi tuyển sinh lớp 10 THPT năm học 2013 môn Toán - Lào Cai.
Đề thi tuyển sinh lớp 10 môn Toán:
SỞ GIÁO DỤC VÀ ĐÀO TẠO ĐỀ THI CHÍNH THỨC | ĐỀ THI TUYỂN SINH LỚP 10 THPT NĂM HỌC 2012-2013 Môn thi: Toán Thời gian: 120 phút không kể thời gian giao đề |
Câu I: (2,5 điểm)
1. Thực hiện phép tính:

![]()
2. Cho biểu thức:
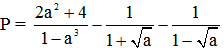
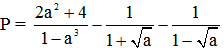
a) Tìm điều kiện của a để P xác định
b) Rút gọn biểu thức P.
Câu II: (1,5 điểm)
1. Cho hai hàm số bậc nhất y = -x + 2 và y = (m+3)x + 4. Tìm các giá trị của m để đồ thị của hàm số đã cho là:
a) Hai đường thẳng cắt nhau
b) Hai đường thẳng song song.
2. Tìm các giá trị của a để đồ thị hàm số y = ax2 (a # 0) đi qua điểm M(-1; 2).
Câu III: (1,5 điểm)
1. Giải phương trình x2 – 7x – 8 = 0
2. Cho phương trình x2 – 2x + m – 3 = 0 với m là tham số. Tìm các giá trị của m để phương trình có hai nghiệm x1; x2 thỏa mãn điều kiện x13x2 + x1x23 = -6
Câu IV: (1,5 điểm)
1. Giải hệ phương trình:
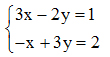
2. Tìm m để hệ phương trình
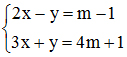 có nghiệm (x; y) thỏa mãn điều kiện x + y > 1.
có nghiệm (x; y) thỏa mãn điều kiện x + y > 1.
Câu V: (3,0 điểm) Cho nửa đường tròn tâm O đường kính AB = 2R và tiếp tuyến Ax cùng phía với nửa đường tròn đối với AB. Từ điểm M trên Ax kẻ tiếp tuyến thứ hai MC với nửa đường tròn (C là tiếp điểm). AC cắt OM tại E; MB cắt nửa đường tròn (O) tại D (D khác B).
a) Chứng minh AMOC là tứ giác nội tiếp đường tròn.
b) Chứng minh AMDE là tứ giác nội tiếp đường tròn.
c) Chứng mình góc ADE = góc ACO




