Bài tập Tam giác cân, tam giác vuông cân lớp 7
Bài tập Toán lớp 7: Tam giác cân - Tam giác vuông cân
Bài tập Tam giác cân, tam giác vuông cân lớp 7 do VnDoc biên soạn sau đây tổng hợp lý thuyết cơ bản, kèm bài tập Toán lớp 7 về Tam giác cân và tam giác vuông cân, giúp các bạn học sinh luyện tập và củng cố về các dạng bài tập liên quan. Qua đó giúp các bạn học sinh ôn tập, củng cố thêm kiến thức đã học trong chương trình Toán lớp 7. Mời các bạn học sinh và quý thầy cô cùng tham khảo chi tiết.
A. Lý thuyết cần nhớ về tam giác cân, tam giác vuông cân
1. Tam giác cân
+ Tam giác cân là tam giác có hai cạnh bằng nhau
2. Tính chất của tam giác cân
+ Tính chất 1: Trong một tam giác cân, hai góc ở đáy bằng nhau
+ Tính chất 2: Một tam giác có hai góc bằng nhau thì là tam giác cân
3. Tam giác vuông cân
+ Tam giác vuông cân là tam giác có 2 cạnh vuông góc và bằng nhau
4. Tính chất của tam giác vuông cân
+ Tính chất 1: Tam giác vuôn cân có hai góc ở đáy bằng nhau và bằng 450
+ Tính chất 2: Các đường cao, đường trung tuyến, đường phân giác kẻ từ đỉnh góc vuông của tam giác vuông cân trùng nhau và bằng 1 nửa cạnh huyền.
Để nắm rõ hơn về định nghĩa tam giác cân, tam giác vuông cân cũng như tính chất về tam giác cân, tam giác vuông cân mời các bạn học sinh tham khảo thêm:
Định nghĩa hình tam giác cân, tam giác vuông cân
B. Các bài toán ôn tập về tam giác cân và tam giác vuông cân
Bài tập trắc nghiệm
Bài tập 1:
Đề bài: Trong các đáp án dưới đây đáp án nào sai
A. Tam giác đều có ba góc bằng nhau và mỗi góc bằng 60°
B. Tam giác đều là tam giác có ba cạnh bằng nhau
C. Tam giác cân là tam giác đều
D. Tam giác đều là tam giác cân đặc biệt.
Đáp án đúng: C. Tam giác cân là tam giác đều- đây là một khẳng định sai
Giải thích:
- Tam giác đều là tam giác có ba cạnh bằng nhau và ba góc đều bằng nhau, mỗi góc có độ lớn 60° (π/3 radian). Tam giác cân là tam giác có hai cạnh bằng nhau và hai góc tại hai đỉnh cân có độ lớn bằng nhau.
- Tam giác đều có thể coi là một trường hợp đặc biệt của tam giác cân, vì tam giác đều không chỉ có hai cạnh bằng nhau mà còn có ba cạnh bằng nhau. Nhưng tam giác cân không nhất thiết phải có ba cạnh bằng nhau, nó chỉ cần có hai cạnh bằng nhau.
Vậy, đáp án C là sai. Tam giác cân không phải là tam giác đều, mà chỉ là một loại tam giác có hai cạnh bằng nhau.
Bài tập 2:
Đề bài: Dựa vào đặc điểm của tam giác cân, hãy chọn đáp án đúng
Tam giác cân là một tam giác mang đặc điểm là:
A. có hai đường cao trong tam giác bằng nhau
B. hai đường trung tuyến có độ dài bằng nhau
C. có hai cạnh bên bằng độ dài với nhau
D. có hai tia phân giác trong cùng số đo
Đáp án đúng: C. Tam giác cân là một tam giác có hai cạnh bên bằng độ dài với nhau
Giải thích:
Tam giác cân là tam giác có hai cạnh bằng nhau và hai góc ở đỉnh cân bằng nhau. Điều này đồng nghĩa với việc tam giác cân có hai cạnh bên (hai cạnh có đỉnh chung) có độ dài bằng nhau.
Các đáp án khác không đúng với định nghĩa của tam giác cân:
A. Hai đường cao của tam giác cân không nhất thiết phải bằng nhau. Đường cao là đoạn thẳng nối một đỉnh của tam giác với đối diện với cạnh đối diện đỉnh đó.
B. Hai đường trung tuyến của tam giác cân không nhất thiết phải bằng nhau. Đường trung tuyến là đoạn thẳng nối một đỉnh của tam giác với trung điểm của cạnh đối diện đỉnh đó.
D. Hai tia phân giác trong của tam giác cân không nhất thiết phải bằng nhau. Tia phân giác trong là tia xuất phát từ một đỉnh của tam giác và chia đôi góc tại đỉnh đó.
Bài tập 3:
Đề bài: Chọn đáp án đúng trong các đáp án sau, biết Tam giác ABC cân tại A, biết rằng số đo góc B là 50o , vậy số đo các góc còn lại của tam giác ABC đã cho là:
A. Góc A = 50o, Góc C = 80o
B. Góc A = 80o, Góc C = 50o
C. Góc A = 40o, Góc C = 90o
D. Góc A = 90o, Góc C = 40o
Đáp án đúng: B- Số đo các góc còn lại trong tam giá cân ABC là Góc A = 80o và Góc C = 50o
Giải thích:
Tam giác ABC là tam giác cân tại A, tức là AB = AC và góc tại đỉnh A có độ lớn là 50o (theo điều kiện trong câu hỏi).
Vì ABC là tam giác cân nên góc B và góc C (góc ở hai đỉnh chân) có độ lớn bằng nhau.
Vì tổng ba góc trong tam giác là 180o, ta có:
Góc B + Góc A + Góc C = 180o
50° + Góc A + Góc C = 180o
Do đó: Góc A + Góc C = 180o - 50o = 130o
Từ đó suy ra, số đo các góc sẽ là: góc B = góc C = 50o, góc A = 130o - góc C = 80o
Bài tập 4:
Đề bài: Chọn đáp án đúng cho câu hỏi dưới đây
Tam giác ABC có hai góc B và góc C = 45o, Vậy tam giác ABC là tam giác gì?
A. Tam giác cân
B. Tam giác vuông
C. Tam giác đều
D. Tam giác vuông cân
Đáp án đúng: D- ABC là tam giác vuông cân
Giải thích:
Tam giác có hai góc B và C bằng 45o, tức là góc B = góc C = 45o.
Vì tổng ba góc trong một tam giác là 180o, ta có: A + B + C = 180o.
Thay vào giá trị góc B = C = 45o, ta có: A + 45o + 45o = 180o.
Từ đó, ta tính được góc A là: A = 180o - 45o - 45o = 90o.
Vậy tam giác ABC có một góc bằng 90o (góc A = 90o) và hai góc bằng nhau (góc B = góc C = 45o), nên đây là tam giác vuông cân.
Bài tập tự luận
Bài 1: Hãy cho biết cần thêm điều kiện gì để
a, Tam giác vuông trở thành tam giác vuông cân
b, Tam giác cân trở thành tam giác vuông cân
Bài 2: Cho tam giác ABC, biết góc ![]() . Tính số đo các góc còn lại của tam giác đó.
. Tính số đo các góc còn lại của tam giác đó.
Bài 3: Cho tam giác ABC cân tại A. Lấy điểm D và E lần lượt là trung điểm của AB và AC. Chứng minh BE = CD
Bài 4: Cho tam giác ABC cân ở A. Trên cạnh BC lấy D, E sao cho BD = CE. Chứng minh tam giác ADE là tam giác cân
Bài 5: Cho tam giác ABC có ![]()
a, Chứng minh tam giác ABC cân
b, Đường thẳng song song với BC cắt tia đối của tia AB ở D, cắt tia đối của tia AC ở E. Chứng minh tam giác ADE cân
Bài 6: Cho tam giác vuông cân ABC tại A, tia phân giác của các góc B và C cắt AC và AB lần lượt tại E và D
a, Chứng minh rằng BE = CD, AD = AE
b, Gọi I là giao điểm của BE và CD, AI cắt BC tại M. Chứng minh rằng các tam giác MAB và MAC là tam giác vuông cân
C. Hướng dẫn giải
Bài 1:
a, Gọi ![]() là tam giác vuông, tức là
là tam giác vuông, tức là ![]()
Để ![]() trở thành tam giác vuông cân tại A thì hai cạnh góc vuông AB = AC
trở thành tam giác vuông cân tại A thì hai cạnh góc vuông AB = AC
b, Gọi ![]() là tam giác cân tại A, tức là ta có AB = AC
là tam giác cân tại A, tức là ta có AB = AC
Để ![]() trở thành tam giác vuông cân tại A thì
trở thành tam giác vuông cân tại A thì ![]()
Bài 2:
Có ![]() là tam giác cân tại A
là tam giác cân tại A ![]()
Lại có theo đề bài ![]()
![]()
Xét ![]() có
có ![]() (tổng 3 góc trong 1 tam giác)
(tổng 3 góc trong 1 tam giác)

Bài 3:
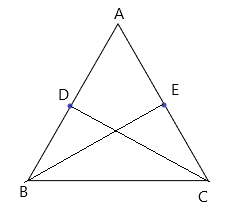
Xét tam giác ABC cân tại A, có ![]() và AB = AC
và AB = AC
Có D là trung điểm của AB ![]() AD = BD
AD = BD
Có E là trung điểm của AC ![]() AE = EC
AE = EC
Từ đó ta có AD = BD = AE = EC
Xét tam giác BDC và tam giác CEB có:
BD = CE (cmt)
![]() (cmt)
(cmt)
BC chung
![]() Hai tam giác BDC và tam giác CEB bằng nhau (theo trường hợp c - g - c)
Hai tam giác BDC và tam giác CEB bằng nhau (theo trường hợp c - g - c)
![]() BE = CD (cặp cạnh tương ứng)
BE = CD (cặp cạnh tương ứng)
Bài 4:
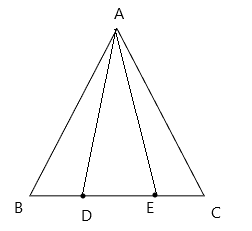
Xét tam giác ABD và tam giác ACE có:
AB = AC (do tam giác ABC cân tại A)
![]() (do tam giác ABC cân tại A)
(do tam giác ABC cân tại A)
BD = EC (giả thiết)
![]() (cặp cạnh tương ứng)
(cặp cạnh tương ứng)
Xét tam gác ADE có AD = AE (cmt). Suy ra tam giác ADE là tam giác cân tại A
Bài 5: Học sinh tự vẽ hình
a, Xét tam giác ABC có: ![]() (tổng ba góc trong một tam giác)
(tổng ba góc trong một tam giác)

Có ![]() Tam giác ABC là tam giác cân tại A
Tam giác ABC là tam giác cân tại A
b, Co ED// BC
![]() (vị trí so le trong) và
(vị trí so le trong) và ![]() (vị trí so le trong)
(vị trí so le trong)
Mà ![]()
Suy ra ![]() Tam giác ADE cân tại A
Tam giác ADE cân tại A
Bài 6: Học sinh tự vẽ hình
a, Vì tam giác ABC cân tại A nên AB = AC và ![]()
Vì BE là tia phân giác của góc B nên ![]()
Và CD là tia phân giác của góc C nên ![]()
Và ![]() nên
nên ![]()
Xét tam giác BEA và tam giác CDA có:
![]() chung
chung
AB = AC (gt)
![]()
Suy ra tam giác BEA bằng với tam giác CDA (theo trường hợp g-c-g)
Suy ra BE = CD và AD = AE (cặp cạnh tương ứng)
b, Có ![]()
Xét tam giác AID và tam giác AIE có:

AI chung
Suy ra tam giác AID bằng tam giác AIE (theo trường hợp c-g-c)
Suy ra ![]() (hai góc tương ứng)
(hai góc tương ứng)
Lại có ![]()
Suy ra hai tam giác AMB và AMC là hai tam giác vuông cân
--------
Trên đây, VnDoc đã gửi tới các bạn Bài tập về tam giác cân và tam giác vuông cân. Hy vọng thông qua tài liệu này, các em sẽ biết cách giải các dạng bài tập liên quan tới tam giác cân và tam giác vuông cân, từ đó nâng cao kỹ năng giải Toán 7 và học tốt Toán 7 hơn.
Ngoài tài liệu trên, mời các bạn tham khảo thêm các tài liệu môn Toán lớp 7 được cập nhật liên tục trên VnDoc.com.