Bài tập Đạo hàm
Bài tập Toán lớp 11: Đạo hàm
Bài tập Đạo hàm Toán lớp 11 vừa được VnDoc.com tổng hợp và xin gửi tới bạn đọc cùng tham khảo. Mời các bạn cùng theo dõi bài viết dưới đây nhé.
1. Đạo Hàm
1.1. Quy Tắc Đạo Hàm
Cho u = u(x), v = v(x), C: là hằng số
- (u + v)' = u' + v'
- (u.v)' = u'.v + v'. u ⇒ (C.u)' = C.u'

- Nếu y = f(x), u = u(x) ⇒ y'x = y'u.u'x
1.2. Công thức Đạo hàm
- (C)' = 0 ; (x)' = 1
- (xn)' = n.xn - 1 ⇒ (un)' = n.un - 1.u'; (n ∈
 , n ≥ 2)
, n ≥ 2) 
- (sin x)' = cos x ⇒ (sin u)' = u' . cos u
- (cos x)' = -sin x ⇒ (cos u)' = -u' . sin u
- (tan x)' =
 ⇒ (tan u)' =
⇒ (tan u)' = 
- (cot x)' =
 ⇒ (cot x)' =
⇒ (cot x)' = 
Tham khảo bài: Bảng đạo hàm cơ bản
1.3. Công thức tính gần đúng:
f(xo + Δx) ≈ f(xo) + f'(xo).Δx
1.4. Viết phương trình tiếp tuyến của đường cong
Tiếp tuyến của đồ thị (C): y = f(x) tại M(xo; yo), có phương trình là: y = f'(xo).(x - xo) + yo.
Khi biết hệ số góc của tiếp tuyến: Nếu tiếp tuyến của đồ thị (C): y = f(x) có hệ số góc là k thì ta gọi M(xo; yo) là tiếp điểm => f'(xo) = k (1)
- Giải phương trình (1) tìm xo suy ra yo f'(xo)
- Phương trình tiếp tuyến phải tìm có dạng: y = k(x - xo) + yo.
Chú ý:
- Hệ số góc của tiếp tuyến tại M(xo; yo) ∈ (C) là k = f'(xo) = tanα. Trong đó α là góc giữa chiều dương của trục hoành và tiếp tuyến.
- Hai đường thẳng song song với nhau thì hệ số góc của chúng bằng nhau.
- Hai đường thẳng vuông góc nếu tích hệ số góc của chúng bằng .
Biết tiếp tuyến đi qua điểm A(x1; y1):
- Viết phương trình tiếp tuyến của y = f(x) tại M(xo; yo): y = f'(xo).(x - xo) + yo. (1)
- Vì tiếp tuyến đi qua A(x1; y1) => y1 = f'(xo).(x1 - xo) + f'(xo) (*)
- Giải phương trình(*) tìm xo thế vào (1) suy ra phương trình tiếp tuyến.
2. Bài tập Đạo hàm lớp 11
Bài 1: Tìm đạo hàm của các hàm số sau:
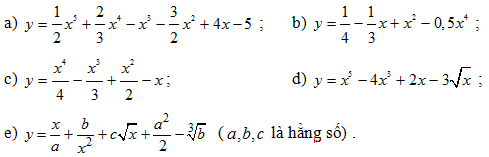
Đáp số:
a. ![]()
b. ![]()
c. y' = x3 - x2 + x - 1
Bài 2: Tìm đạo hàm của các hàm số sau:
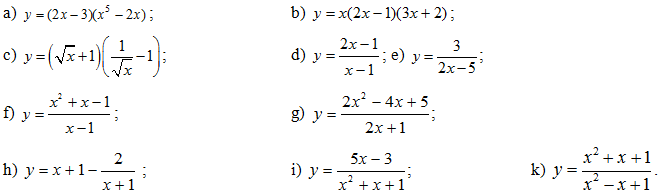
Đáp số:
| a. y' = 12x5 - 8x -15x4 + 6 | b. y' = 18x2 + 2x - 2 |
| c. | d. y' = -1/(x- 1)2 |
| e. y' = -6/(2x - 5)2 | f. y' = (x2 - 2x -1)/(x - 1)2 |
| g. y'=(8x3 - 8x2 + 4x - 10)/(2x + 1)2 | h. y' = 1 + 2/(x + 1)2 |
| i. y' = (-5x2 + 6x + 8)/(x2 + x + 1)2 | k. y' = (-5x2 + 6x + 8)/(x2 - x + 1)2 |
Bài 3: Tìm đạo hàm của các hàm số sau:
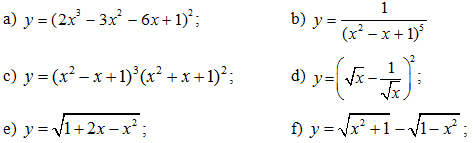
Bài 4: Cho hàm số ![]() . Xác định giá trị của tham số m để:
. Xác định giá trị của tham số m để:
a. y' ≤ 0, ∀ x∈ ![]()
b. y' = 0 có hai nghiệm phân biệt cùng âm.
c. y' = 0 có hai nghiệm phân biệt thỏa mãn điều kiện x12 + x22 = 3.
Bài 5: Cho hàm số (C): y = mx4 + (m2 - 9)x2 + 10 (1) (m là tham số). Xác định giá trị của m để hàm số có y' = 0 có 3 nghiệm phân biệt.
Bài 6: Cho hàm số (C): y = x2 - 2x + 3. Viết phương trình tiếp tuyến với (C):
a. Tại điểm có hoành độ x0 = 2
b. Biết tiếp tuyến song song với đường thẳng 4x - y = 9
c. Vuông góc với đường thẳng 2x + 4y - 2011 = 0
d. Biết tiếp tuyến đi qua điểm A(1; 0)
Bài 7: Cho hàm số: ![]() (1).
(1).
a. Viết phương trình tiếp tuyến của (C) tại điểm M(-1;-1)
b. Viết phương trình tiếp tuyến của (C) tại giao điểm của (C) với trục hoành.
c. Viết phương trình tiếp tuyến của (C) tại giao điểm của (C) với trục tung.
d. Viết phương trình tiếp tuyến của (C) biết tiếp tuyến song song với đường thẳng (d): 4x - y + 1 = 0
e. Viết phương trình tiếp tuyến của (C) biết tiếp tuyến vuông góc với đường thẳng (d'): 4x + y - 8 = 0
Bài 8: Cho hàm số y = x3 - 3x2 (C)
a. Viết phương trình tiếp tuyến của đồ thị (C) tại điểm I(1;-2)
b. Chứng minh rằng các tiếp tuyến khác của đồ thị (C) không đi qua I.
Bài 9: Cho hàm số: ![]() (1). Tính diện tích tam giác tạo bởi các trục tọa độ và tiếp tuyến của đồ thị hàm sô (1) tại điểm M(-2; 5).
(1). Tính diện tích tam giác tạo bởi các trục tọa độ và tiếp tuyến của đồ thị hàm sô (1) tại điểm M(-2; 5).
Bài 10: Cho hàm số (C): ![]() . Tìm điểm M thuộc (C), biết tiếp tuyến của (C) tại M cắt hai trục tọa độ tại A, B và tam giác OAB có diện tích bằng 2.
. Tìm điểm M thuộc (C), biết tiếp tuyến của (C) tại M cắt hai trục tọa độ tại A, B và tam giác OAB có diện tích bằng 2.
Bài 11:
a. Viết phương trình tiếp tuyến của đồ thị hàm số: y = x4 - 2x2 + 5 tại điểm A(2;13).
b. Viết phương trình tiếp tuyến của đồ thị hàm số y = x3 - 3x2 + 2 biết tiếp tuyến song song với d có phương trình y = -3x + 2
c. Viết phương trình tiếp tuyến của đồ thị hàm số y = x3 - 3x2 + 2 biết tiếp tuyến song song với d có phương trình y = -3x + 2
d. Cho hàm số y = 3x3 + x2 - 2 có đồ thị C. Phương trình tiếp tuyến của C tại điểm có hoành độ là nghiệm của phương trình y" = 0 là bao nhiêu?
e. Phương trình tiếp tuyến của đồ thị hàm số: y = x3 - 3x + 1 tại điểm có hoành độ = 1 có hệ số góc là k bằng bao nhiêu? Tìm điểm cực tiểu của hàm số: y = -x2 + 2x - 1?
---------------------------------------------------------
Trên đây VnDoc.com vừa giới thiệu tới các bạn bài viết Bài tập Toán lớp 11: Đạo hàm. Bài viết giới thiệu tới chúng ta các kiến thức đạo hàm cần nhớ và một số các dạng bài tập đạo hàm trong chương trình lớp 11. Mong rằng qua đây các bạn có thêm thật nhiều tài liệu để phục vụ cho việc học tập nhé. Mời các bạn cùng theo dõi thêm.
- Lý thuyết và bài tập Toán 11: Hàm số liên tục
- Lý thuyết và bài tập Toán 11: Giới hạn của hàm số
- Công thức toán học giải nhanh Đạo hàm
- 11 đề ôn tập hè môn Toán lớp 11
- Bài tập xác suất lớp 11 có đáp
Để học tốt môn Toán lớp 11, mời các bạn tham khảo thêm các chuyên mục:






