Đề thi chọn học sinh giỏi cấp trường Toán 10 năm 2018 - 2019 trường THPT Yên Phong số 2 - Bắc Ninh
Đề thi chọn HSG lớp 10 môn Toán có đáp án
SỞ GD&ĐT BẮC NINH
TRƯỜNG THPT YÊN PHONG SỐ 2
ĐỀ CHÍNH THỨC
Đề gồm có : 01 trang
ĐỀ THI HỌC SINH GIỎI CẤP TRƯỜNG
Năm học : 2018 – 2019
Môn: Toán Lớp: 10
Thời gian làm bài: 150 phút ( Không kể thời gian phát đề)
Ngày thi: 26/01/2019
Câu 1 (4 điểm). Cho hàm số
2
(2 3) 2 2y x m x m
(1)
1) Xét sự biến thiên và vẽ đồ thị hàm số (1) khi m = 0.
2) Xác định m để đồ thị hàm số (1) cắt đường thẳng
3 1y x
tại hai điểm A, B
phân biệt sao cho
OAB
vuông tại O ( với O là gốc toạ độ).
Câu 2 (2 điểm). Tìm tất cả các giá trị của tham số m để hàm số
2
1
2
x
y x m
x m
xác định trên khoảng ( - 1; 3).
Câu 3 (5 điểm). Giải các phương trình sau
2
3 2
1) 3 1 7 2
2) 3 1 4 3 5 4
3) 3 3 5 2 3 10 26 0.
x x x
x x x
x x x x x
Câu 4 (2 điểm). Giải hệ phương trình:
2 3 2
4 2
1
(2 1) 1
x x y xy xy y
x y xy x
Câu 5 (3 điểm). Cho tam giác ABC có AB = 1, AC = x và
0
60 .BAC
Các điểm M, N
được xác định bởi
2MC MB
và
2NB NA
. Tìm x để AM và CN vuông góc với
nhau.
Câu 6 (2 điểm). Cho tam giác ABC. Chứng minh rằng với G là trọng tâm tam giác ABC ta
có
2 2 2
1
. . . ( )
6
GAGB GBGC GC GA AB BC CA
.
Câu 7 (2 điểm). Cho
, , [2018;2019]x y z
. Tìm giá trị lớn nhất của biểu thức:
| 2018.2019 | | 2018.2019 | | 2018.2019 |
( , , )
( ) ( ) ( )
xy yz zx
f x y z
x y z y z x z x y
.
--------------------- Hết ---------------------
Họ và tên thí sinh:........................................... Số báo danh: ................................
Thí sinh không được sử dụng tài liệu. Cán bộ coi thi không giải thích gì thêm.

SỞ GD&ĐT BẮC NINH
TRƯỜNG THPT YÊN PHONG SỐ 2
HƯỚNG DẪN CHẤM HỌC SINH GIỎI CẤP TRƯỜNG
Năm học : 2018 – 2019
Môn: Toán Lớp: 10
Ngày thi: 26/01/2019
Câu Nội dung Điểm
1)Xét sự biến thiên và vẽ đồ thị hàm số (1) khi m = 0.
2,0
1(4đ)
2) Phương trình hoành độ giao điểm:
2
2 2 3 0(*)x mx m
* Tìm được điều kiện để dường thẳng cắt đồ thị hàm số tai A, B là
3m
hoặc
1m
* Gọi
1 2
,x x
là các nghiệm pt (*), ta có
1 2
1 2
2
2 3
x x m
x x m
*
1 1 2 2
( ;3 1), ( ;3 1)A x x B x x
. Tính được
1 2 1 2
. 0 10 3( ) 1 0
31
26 31 0
26
OAOB x x x x
m m
Kết luận
31
26
m
0.5
1
0.5
Hàm số xác định khi
1 0 1
2 0 2
x m x m
x m x m
Tập xá định của hàm số là
[ 1;2 )D m m
với điều kiện
1 2 1.m m m
1
2(2đ)
Hàm số xác định trên
( 1;3)
khi và chỉ khi
( 1; 3) [ 1;2 )
0
1 1 3 2
3
2
m m
m
m m
m
. Vô nghiệm.
Kết luận không có giá trị của m
1
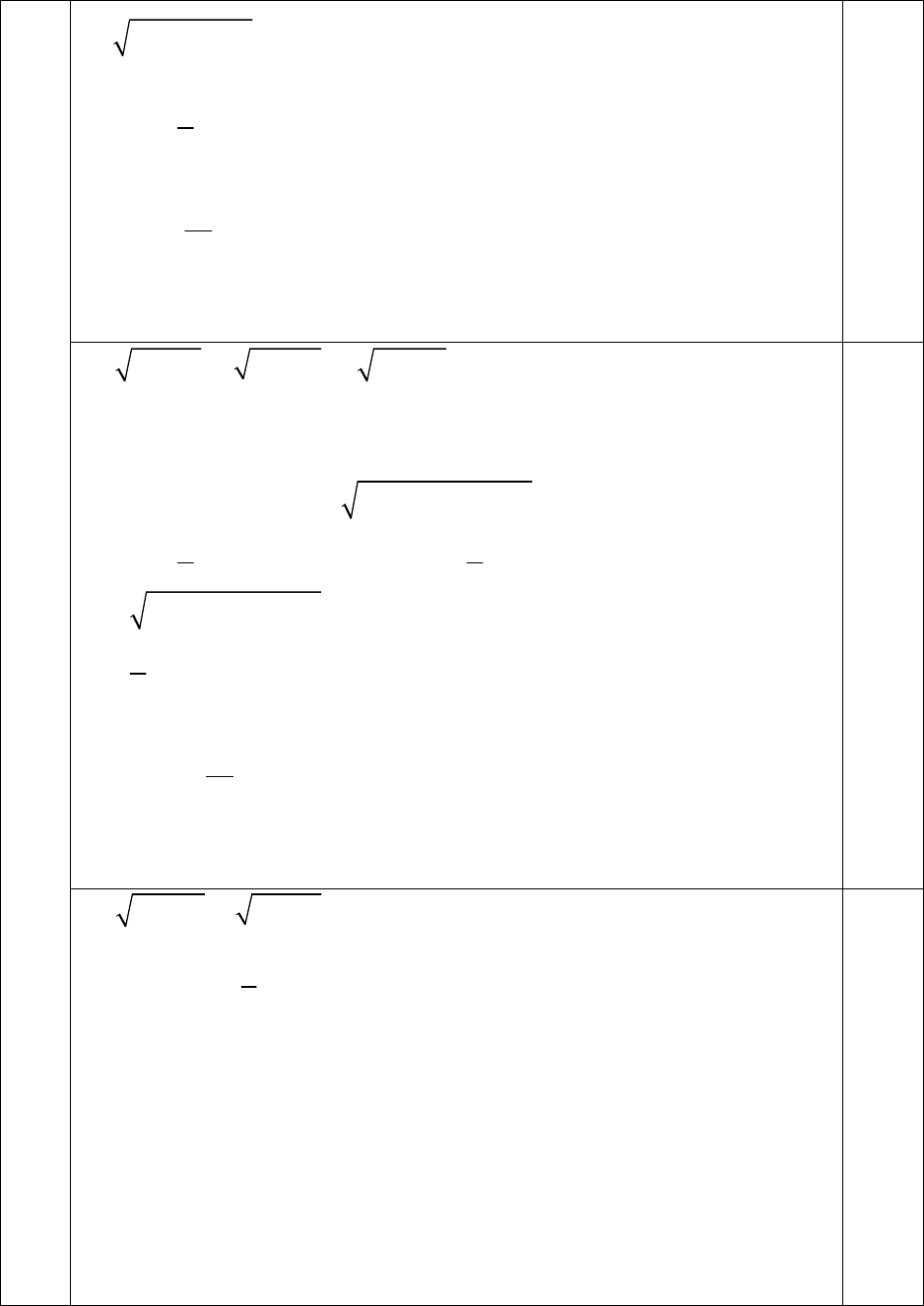
2
2 2
2 7 0
1) 3 1 7 2
3 1 (2 7)
7
2
5
5
10
3
x
x x x
x x x
x
x
x
x
Kết luận
5S
.
2
2
2) 3 1 4 3 5 4
3 1 0
4 3 0
3 1 4 3 2 (3 1)(4 3) 5 4
3 3
3
4 4
(3 1)(4 3) 3 11 12 0
3
3
4
1
1
12
11
x x x
x
x
x x x x x
x x
x x x x x
x
x
x
x
Kết luận Kết luận
1S
.
2
3(5đ)
3 2
3) 3 3 5 2 3 10 26 0.x x x x x
Đk:
5
1
2
x
.
Phương trình viết lại:
1
Đề thi chọn học sinh giỏi lớp 10 môn Toán
VnDoc xin giới thiệu tới bạn đọc Đề thi chọn học sinh giỏi cấp trường Toán 10 năm 2018 - 2019 trường THPT Yên Phong số 2 - Bắc Ninh. Nội dung tài liệu kèm theo đáp án sẽ giúp các bạn học tốt Toán 10 hiệu quả hơn. Mời các bạn tham khảo.
- Đề thi chọn học sinh giỏi tỉnh môn Toán lớp 10 năm học 2017 - 2018 Sở GD&ĐT Hà Tĩnh
- Đề thi chọn học sinh giỏi tỉnh môn Toán lớp 10 năm 2017 - 2018 Sở GD&ĐT Hải Dương
- Đề thi học kì 1 lớp 10 môn Toán năm 2018 - 2019 trường THPT Hoa Lư A - Ninh Bình
- Đề thi học kì 1 lớp 10 môn Toán năm 2018 - 2019 trường THPT Phúc Thọ - Hà Nội
- Đề thi học kì 1 lớp 10 môn Toán năm 2018 - 2019 trường THPT Nguyễn Thị Minh Khai - TP Hồ Chí Minh
-----------------------------
Trên đây VnDoc đã giới thiệu tới các bạn Đề thi chọn học sinh giỏi cấp trường Toán 10 năm 2018 - 2019 trường THPT Yên Phong số 2 - Bắc Ninh. Để có kết quả cao hơn trong học tập, VnDoc xin giới thiệu tới các bạn học sinh tài liệu Giải bài tập Toán 10, Giải bài tập Vật Lí 10, Giải bài tập Sinh học 10, Giải bài tập Hóa học 10, Tài liệu học tập lớp 10 mà VnDoc tổng hợp và đăng tải.







