Đề thi chọn học sinh giỏi lớp 10 môn Toán năm 2018 - 2019 trường THPT Thị xã Quảng Trị
Đề thi HSG Toán 10 có đáp án

SỞ GD&ĐT QUẢNG TRỊ KỲ THI CHỌN HSG VĂN HÓA LỚP 10, 11
TRƯỜNG THPT THỊ XÃ QUẢNG TRỊ Khóa thi ngày 03 tháng 4 năm 2019
Môn thi: Toán lớp 10
Thời gian làm bài: 180 phút, không kể thời gian giao đề
Câu I. (5,0 điểm)
Cho Parabol (P):
2
yx bxc.
1) Tìm
,bc để Parabol (P) có đỉnh
15
;
24
S
.
2) Với
,bc
tìm được ở câu 1. Tìm m để đường thẳng :2
y
xm cắt Parabol (P) tại hai
điểm phân biệt
,AB sao cho tam giác
OAB
vuông tại
O
(với
O
là gốc tọa độ).
Câu II.
(6,0 điểm)
1) Tìm m để bất phương trình:
2
232140mx m x m vô nghiệm trên tập số thực.
2) Giải bất phương trình sau trên tập số thực:
22
24 2 560.xxxx
3) Giải hệ phương trình sau trên tập số thực :
23 2
42
1
211
x
x y xy xy y
xyxyx
Câu III. (6,0 điểm)
1)
Cho tam giác
A
BC đều có độ dài cạnh bằng 3. Trên các cạnh
, BC CA
lần lượt lấy các điểm
, NM
sao cho
1, 2.BN CM
a) Phân tích véc tơ
A
N
theo hai vectơ
, .
A
BAC
b) Trên cạnh
A
B
lấy điểm
,
P
,
P
AP Bsao cho
A
N vuông góc với .
P
M Tính tỉ số .
A
P
A
B
2) Trong mặt phẳng tọa độ Oxy , cho hình thang cân
A
BCD có hai đáy là ,
A
DBC và
A
DBC ,
biết rằng
,7.AB BC ADĐường chéo
A
C có phương trình là 330
x
y, điểm
2; 5M
thuộc đường thẳng
.
A
D Tìm tọa độ đỉnh D biết đỉnh
1;1 .B
Câu IV. (3,0 điểm)
1 ) Cho tam giác
A
BC có diện tích S và bán kính của đường tròn ngoại tiếp
R
thỏa mãn hệ thức
23 3 3
2
= sin sin sin
3
SR A B C
. Chứng minh tam giác
A
BC là tam giác đều.
2) Cho ,,
x
yz là các số thực dương thỏa mãn điều kiện
222
3.xyz Chứng minh rằng
9
.
xyz
yzxxyz
3) Cho đa thức
2018 2016
Px x mx m trong đó m là tham số thực. Biết rằng
P
x có 2018
nghiệm thực. Chứng minh rằng tồn tại một nghiệm thực
0
x
của
P
x thỏa mãn
0
2.x
---------------------HẾT---------------------
Thí sinh không được sử dụng tài liệu và MTCT.
Giám thị không giải thích gì thêm.
Họ và tên thí sinh:
……………………………….Số báo danh:……………….
ĐỀ THI CHÍNH THỨC
(Đề có 01 trang)
HƯỚNG DẪN CHẤM HSG 10 NĂM HỌC 2018-2019.
CÂU NỘI DUNG ĐIỂM
Câu I
(5,0 điểm)
1) (2,0 điểm).
Đỉnh
/2 1/2
1
15
;()
15
1
24
42 4
b
b
SP
b
c
c
2) (3,0 điểm).
Pt hoành độ giao điểm của (P) và
:
22
12 3 10xx xm x xm
(*). cắt (P) tại hai điểm phân biệt
PT(*)
có hai nghiệm phân biệt
12
,
x
x
13
0134 0 **
4
mm
Giả sử
11 2 2
;2 ; ;2
A
xxmBxxm
theo Viet ta có
12
12
3
1
xx
xx m
.
Ta có tam giác
OAB vuông tại
O
22
12 1 2
121
.05 2 0 50 .
2
OA OB x x m x x m m m m
Đối chiếu đk (**) ta có đáp số
121
.
2
m
2
0,5
0,5
0,5
0,5
1
Câu II
(6,0 điểm)
1) (2,0 điểm) TH 1:
0m , bpt trở thành
7
6140
3
xx
(không thỏa ycbt).
TH 2: 0m ,
2
232140mx m x mVN
2
232140mx m x m CN
x
2
0
00
9.
'0 9 1
890
m
mm
m
m hoac m
mm
Vậy
9.m
2)
(2,0 điểm). TH1:
2
2
560
3
x
xx
x
TH 2:
2
2
560
3
x
xx
x
. Khi đó, bpt
2
2
2
20
20
24 2
24 2
x
x
xx
xx
2
2
2
0
2
2
4
40
40
x
x
x
x
x
x
xx
xx
.
Vậy tập nghiệm bất phương trình
;0 2,3 4;S
0,5
0,5
1
0,5
0,5
0,5
0,5
3) (2,0 điểm) Hpt:
22
23 2
2
42
2
1
1
211
1
x
yxyx y xy
xxyxyxyy
xyxyx
xy xy
Đặt
2
,ax ybxy hệ thành
32
2
2
1
20 0 1 2
.
10 3
1
1
aabb
aa a a a a
bbb
ab
ba
0,5
0,5
+) Với
0
1
a
b
ta có
2
0
1.
1
xy
xy
xy
+) Với
1
0
a
b
ta có
2
1
;0;1,1;0,1;0.
0
xy
xy
xy
+) Với
2
3
a
b
ta có
2
2
3
1
2
.
3
3
130
y
x
xy
x
y
xy
xxx
Vậy hệ có 5 nghiệm
; 1;1,0;1,1;0,1;0,1;3.xy
0,5
0,5
Câu III
(6,0 điểm)
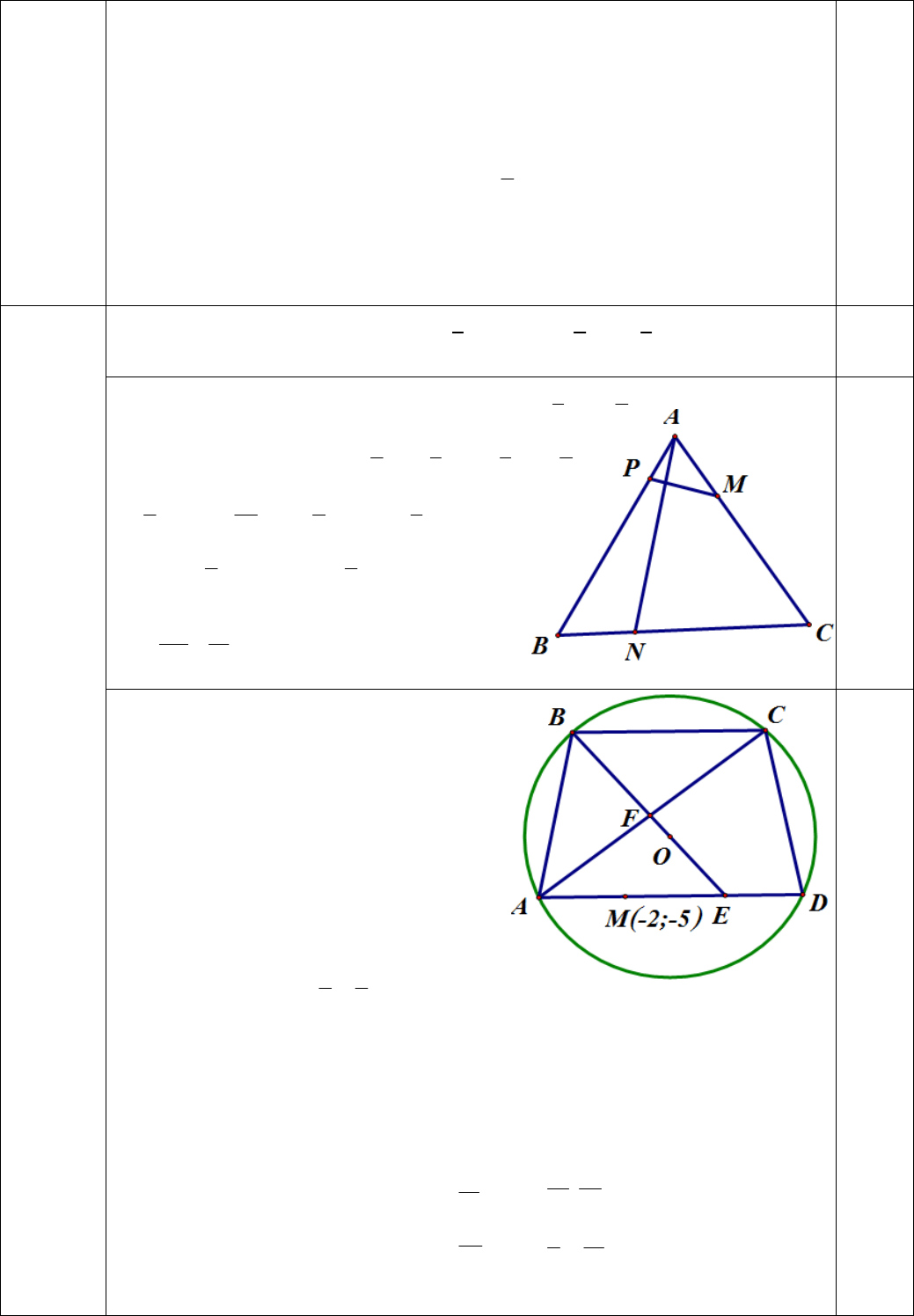
1) (4,0 điểm)
a)
121
= = +
333
A
NABBNAB ACAB AB AC
2,0
b) Đặt
,0 3AP x x. Ta có
1
= -
33
x
P
MPAAM AC AB
22
21 1
.0 . 0
33 33
22 1
.. 0
9999
4
12 1 0
25
x
AN PM AN PM AB AC AC AB
xx
AB AC AB AB AC AC
x
xx
Vậy
4
.
15
AP
A
B
0,5
0,5
0,5
0,5
2) (2,0 điểm). Do ABCD là hình thang cân
nên ABCD là hình thang nội tiếp đường tròn
tâm O.Do
A
BBCCD AClà đường
phân giác trong góc
BAD
. Gọi E là
điểm đối xứng của B qua AC, khi đó
E thuộc AD. Ta có
B
EAC
và
B
E qua
1; 1B nên phương trình
BE:
340xy
.
Gọi
FACBE
tọa độ F là nghiệm của
Hệ
330
31
;.
340
22
xy
F
xy
Do F là trung điểm
Của
2; 2 .BE E Do
2; 5MAD phương trình AD: 3 4 14 0.xy
Do
AADACtọa độ A là nghiệm của hệ
330
6;1 .
34140
xy
A
xy
Do
24;23DAD D t t và
22
58 26
12
;
55
5
744 3349
2
216
;
5
55
D
t
AD t t
t
D
Do B,D nằm khác phía với đường thẳng AC nên kiểm tra vị trí tương đối của điểm
0,5
0,5
0,5
Đề thi chọn học sinh giỏi môn Toán lớp 10
VnDoc xin giới thiệu tới bạn đọc Đề thi chọn học sinh giỏi lớp 10 môn Toán năm 2018 - 2019 trường THPT Thị xã Quảng Trị. Tài liệu gồm 4 câu hỏi bài tập, thời gian làm bài 180 phút, đề thi có đáp án. Mời các bạn học sinh tham khảo.
- Đề thi chọn học sinh giỏi lớp 10 môn Toán năm 2018 - 2019 Sở GD&ĐT Hà Nam
- Đề thi chọn học sinh giỏi lớp 10 môn Toán năm 2018 - 2019 trường THPT Phùng Khắc Khoan - Hà Nội
- Đề thi chọn học sinh giỏi lớp 10 môn Toán năm 2018 - 2019 trường THPT Đan Phượng - Hà Nội
- Đề thi chọn học sinh giỏi lớp 10 môn Toán năm 2018 - 2019 trường THPT Nam Tiền Hải - Thái Bình
- Đề thi chọn học sinh giỏi lớp 10 môn Toán năm 2018 - 2019 Sở GD&ĐT Hà Nam
- Đề thi chọn học sinh giỏi lớp 10 môn Toán cấp tỉnh năm 2018 - 2019 Sở GD&ĐT Hải Dương
Trên đây VnDoc đã giới thiệu tới các bạn Đề thi chọn học sinh giỏi lớp 10 môn Toán năm 2018 - 2019 trường THPT Thị xã Quảng Trị. Để có kết quả cao hơn trong học tập, VnDoc xin giới thiệu tới các bạn học sinh tài liệu Giải bài tập Toán 10, Giải bài tập Vật Lí 10, Giải bài tập Sinh học 10, Giải bài tập Hóa học 10, Tài liệu học tập lớp 10 mà VnDoc tổng hợp và đăng tải.