Đề thi chọn học sinh giỏi lớp 12 môn Toán năm 2018 - 2019 cụm trường THPT Yên Dũng - Bắc Giang
Đề thi HSG Toán 12
SỞ GD&ĐT BẮC GIANG
CỤM TRƯỜNG THPT HUYỆN YÊN DŨNG
KỲ THI CHỌN HỌC SINH GIỎI CẤP CỤM
NĂM HỌC 2018 - 2019
MÔN: TOÁN 12
Thời gian làm bài: 120 phút.
Mã đề: 121
Họ, tên thí sinh: ............................................................. Số báo danh: .......................
(Thí sinh không được sử dụng tài liệu)
PHẦN TRẮC NGHIỆM: (14.0 điểm)
Câu 1: Bất phương trình
3 1
3
2log 4 3 log 2 3 2
x x
có tập nghiệm là:
A.
3
3
4
x
. B.
3
3
8
x
. C.
3
3
4
x
. D.
S
.
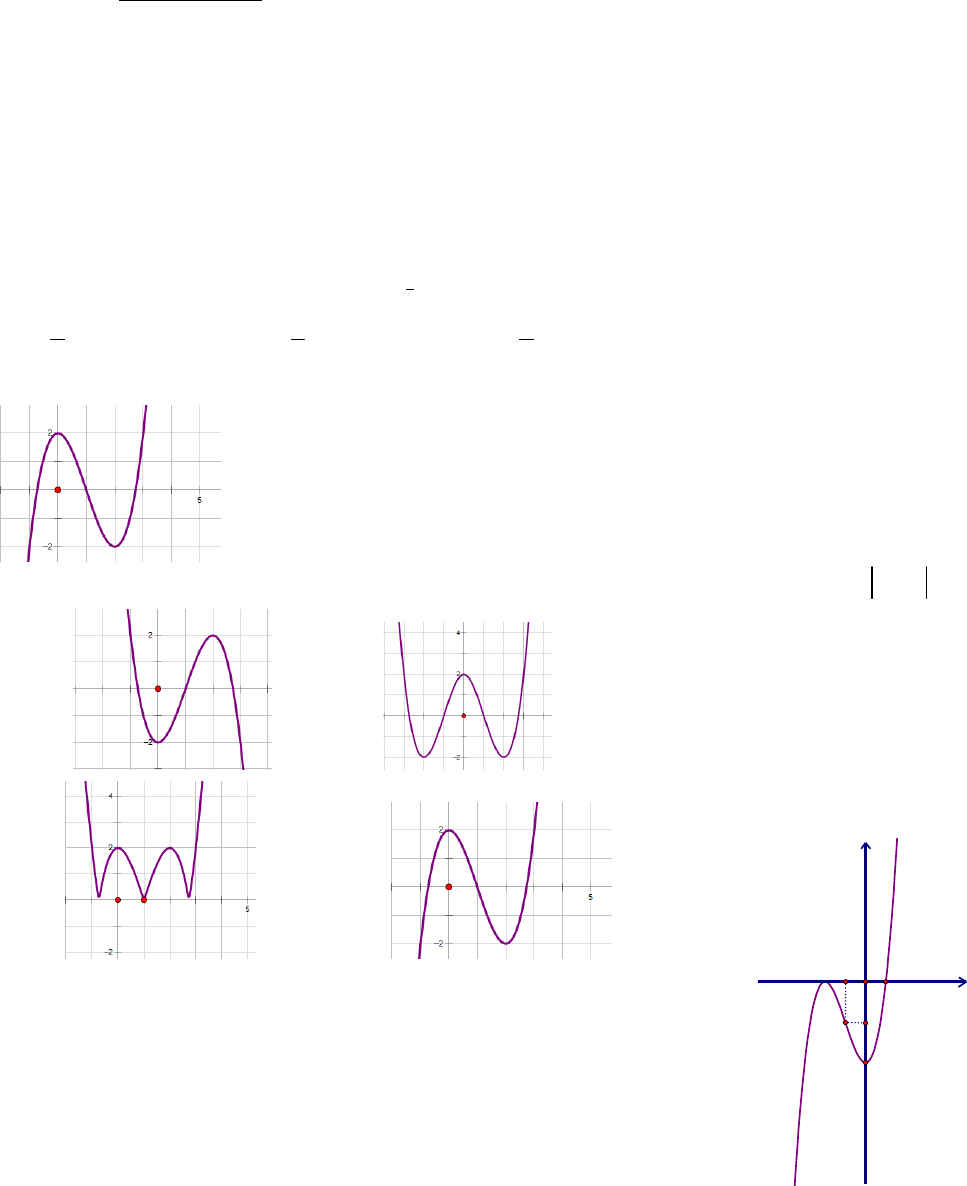
Câu 2: Cho đồ thị hàm số
y f x
như hình dưới đây.
Trong các đồ thị ở các phương án A, B, C, D dưới đây đồ thị nào là đồ thị của hàm số
y f x
?
A. B.
C. D. .
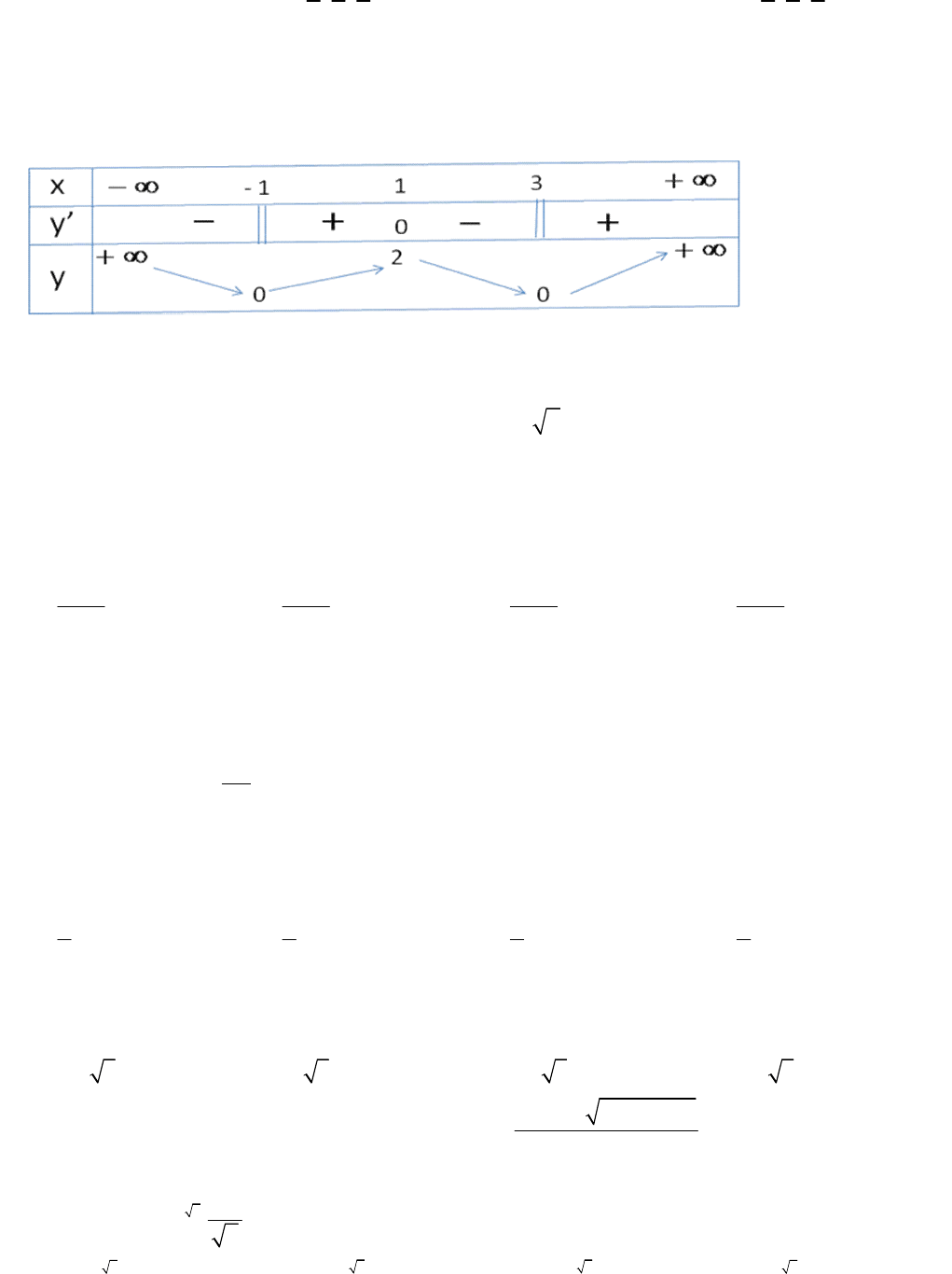
Câu 3: Hình vẽ dưới đây là đồ thị của hàm số
3 2
y ax bx c
: Phương án nào
sau đây là đúng?
A.
2; 3; 4
a b c
. B.
1; 3; 4
a b c
.
C.
1; 3; 4
a b c
. D.
1; 3; 4
a b c
.
Câu 4: Phương trình
2 2
6 3 5 3
2 2.2 2 2 0
x x x x x
có tổng các nghiệm bằng:
A. -5. B. -7. C. 10. D. 0.
Câu 5: Có bao nhiêu cách phân công 4 thầy giáo dạy toán vào dạy 12 lớp 12, mỗi thầy dạy đúng 3 lớp?
A. 369600. B. 396900. C. 220. D. 369000.
Câu 6: Cho hàm số
2
lny x
. Hệ thức nào sau đây đúng?
A.
2
'' ' 2
x y xy
. B.
2
'' ' 2
x y xy
. C.
2
'' ' 2
x y xy
. D.
2
'' ' 2
x y xy
.
Câu 7: Trong không gian với hệ tọa độ Oxyz, cho tam giác ABC biết A(1;2;-1), B(2;1;1), C(0;1;2). Tìm
tọa độ tâm I của đường tròn ngoại tiếp của tam giác ABC.
y
x
-4
O
1
-1
I
-2
A. I(-2;1;1). B.
1 3 1
; ;
2 2 2
I
. C. I(1;1;2). D.
3 1 1
; ;
2 2 2
I
.
Câu 8: Nếu
1 1
f
,
f x
là hàm số liên tục trên
và
5
1
' 10
f x dx
. Khi đó
5f
có giá trị là:
A. 9. B. 12. C. 11. D. 10.
Câu 9: Cho hàm số y = f(x) xác định trên
và có bảng biến thiên như hình vẽ:
Chọn khẳng định đúng ?
A. Hàm số có 2 điểm cực trị . B. Hàm số có 1 điểm cực trị.
C. Hàm số có 3 điểm cực trị. D. Hàm số không có điểm cực trị.
Câu 10: Giá trị nhỏ nhất và lớn nhất của hàm số
2y x x
trên đoạn
[0;9]
lần lượt là
m
và
M
. Giá
trị của tổng
m M
bằng
A.
2
B.
3
C.
0
D.
1
.
Câu 11: Một trường THPT có 18 học sinh đạt giải học sinh giỏi cấp tỉnh, trong đó có 11 học sinh nam và
7 học sinh nữ. Chọn ngẫu nhiên 6 học sinh trong số các học sinh trên đi tham quan học tập tại Hà Nội.
Tính xác suất để có ít nhất một học sinh nam và một học sinh nữ được chọn.
A.
2559
2652
. B.
2855
2652
. C.
2538
2652
. D.
2585
2652
.
Câu 12: Một chất điểm chuyển động thẳng xác định bởi phương trình
3 2
3 4S f t t t t
, trong đó t
được tính bằng giây (s) và S được tính bằng mét (m). Gia tốc của chất điểm tại thời điểm
2t s
có giá trị
bằng:
A.
2
4 /m s
. B.
2
6 /m s
. C.
2
12 /m s
D.
2
8 /m s
.
Câu 13: Phương trình
5 3
2 .5 2000
x
x
x
có một nghiệm được viết dưới dạng
log
a
x b
với
,a b
là hai số
nguyên dương có ước chung lớn nhất bằng 1 và nhỏ hơn 10. Khi đó
a b
có giá trị là:
A. 6. B. 10. C. 5. D. 7.
Câu 14: Tìm m để hàm số
4 2
1 2 1 1
y m x m x
có đúng 3 điểm cực trị.
A.
1
1
2
m
. B.
1
1
2
m
. C.
1
1
2
m
. D.
1
1
2
m
.
Câu 15: Cho hình chóp S.ABC có đáy ABC là tam giác cân tại A,
4 ; 6AB AC a BC a
.Hình chiếu
vuông góc của S trên mặt phẳng (ABC) nằm trong tam giác ABC. Các mặt bên của hình chóp cùng tạo
với đáy góc 60
0
. Tính thể tích khối chóp S.ABC.
A.
3
6 3
a . B.
3
3
a . C.
3
8 3
a . D.
3
3 3
a .
Câu 16: Số đường tiệm cận đứng của đồ thị hàm số
2
2
4 1 2 6
2
x x x
y
x x
là:
A. 3. B. 2. C. 1. D. 0.
Câu 17: Cho
ln 2
2 .
x
I dx
x
. Khi đó kết quả nào sau đây sai?
A.
1
2
x
I C
. B.
2 2 1
x
I C
. C.
2 2 1
x
I C
. D. 2
x
I C
.
Câu 18: Trong không gian với hệ tọa độ Oxyz , cho hai véc tơ
2
log 7; ; 1
a m
và
7
log 4;1;3
b
.
Tìm m để
a b
.
A.
1
m
. B.
1
m
. C.
2
m
. D.
2
m
.
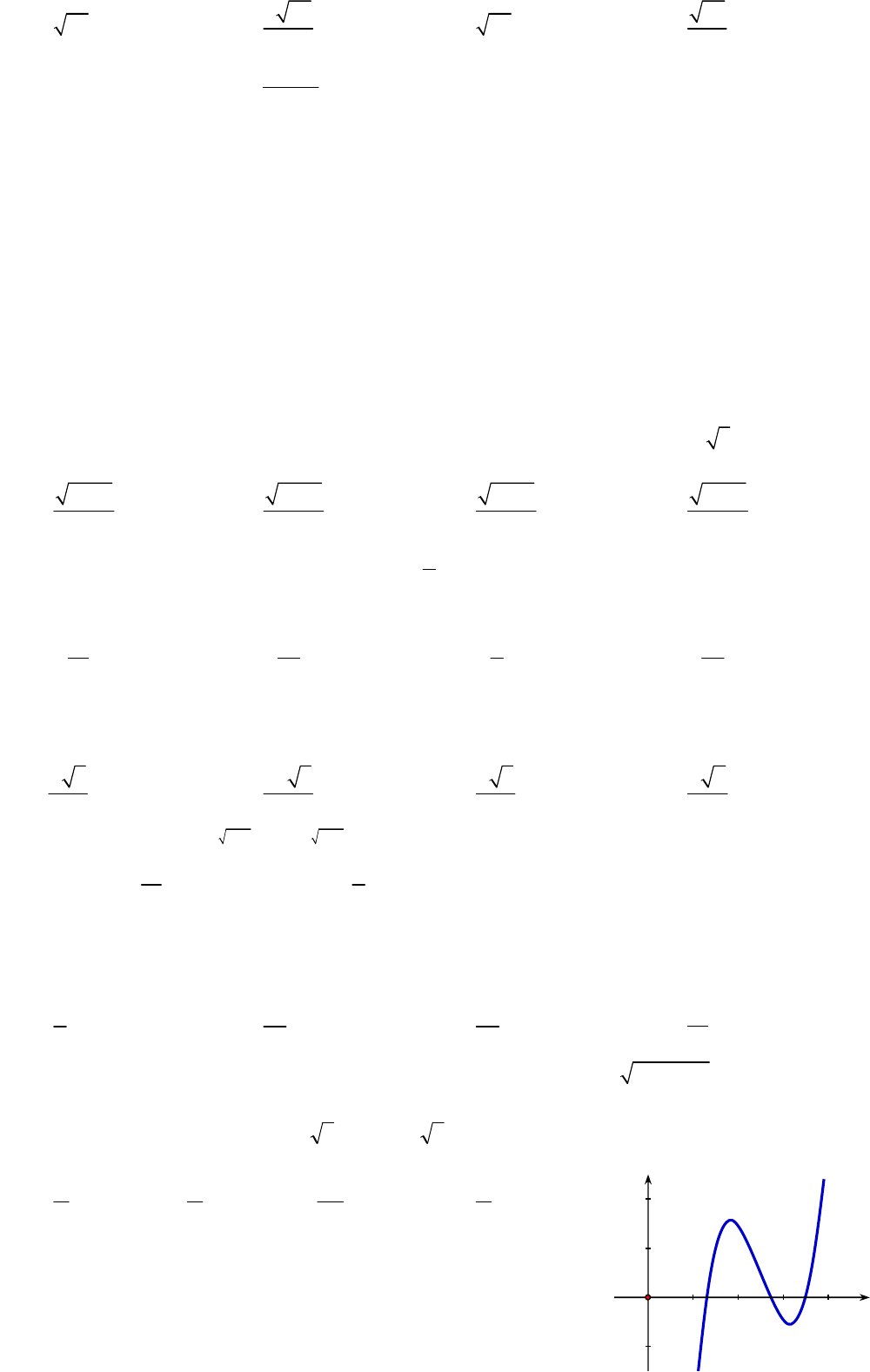
Câu 19: Trong không gian với hệ tọa độ Oxyz, cho tam giác ABC có
1;2; 1
A
,
2; 1;3
B
,
4;7;5
C
. Độ dài đường phân giác trong kẻ từ đỉnh B là?
A.
74
. B.
2 74
3
. C.
26
. D.
74
3
.
Câu 20: Tìm m để hàm số
4
mx
y
x m
đồng biến trên khoảng
1;
.
A.
2
m
. B.
2 2
m
. C.
2
2
m
m
. D.
2
m
.
Câu 21: Tìm trên đường thẳng
2
x
các điểm mà từ đó kẻ được đúng hai tiếp tuyến đến đồ thị
3
( ) : 3C y x x
.
A.
2;2 ;N 2; 6
M
. B.
1; 3 ; N 2;3
M
. C.
1;3 ; N 2; 3
M
. D.
2; 3 ; N 2;3
M
.
Câu 22: Cho
2
F x x
là một nguyên hàm của hàm số
2x
f x e
. Tìm nguyên hàm của hàm số
2
'
x
f x e
.
A.
2 2
' 2 2
x
f x e dx x x C
. B.
2 2
' 2
x
f x e dx x x C
.
C.
2 2
'
x
f x e dx x x C
. D.
2 2
' 2 2
x
f x e dx x x C
.
Câu 23: Cho tứ diện ABCD có các cạnh AD=BC=
3
; AC=BD=
4
; AB=CD=
2 3
. Thể tích tứ diện
ABCD bằng:
A.
2047
12
B.
2074
12
C.
2740
12
D.
2470
12
.
Câu 24: Cho hàm số
f x
thỏa mãn
2
2
9
f
và
2
' 2
f x x f x
với mọi
x
. Giá trị của
1f
bằng:
A.
2
15
. B.
19
36
. C.
2
3
. D.
35
36
.
Câu 25: Cho hình chóp S.ABCD có SAB là tam giác đều, mặt phẳng (SAB) vuông góc với đáy, đáy
ABCD là hình vuông cạnh a. Gọi M, N lần lượt là trung điểm của BC và SD. Khoảng cách giữa DM và
CN là:
A.
3
8
a
. B.
2 3
5
a
. C.
5
8
a
. D.
7
8
a
.
Câu 26: Phương trình
2 2
1 1
9 8.3 4
x x x x
m
có nghiệm khi :
A.
13
12
9
m
. B.
7
12
9
m
. C.
12 1
m
. D.
12 2
m
.
Câu 27: Gọi S là tập hợp các số tự nhiên có 3 chữ số được lập từ tập
0;1;2;3;4;5;6;7
X
.Rút ngẫu
nhiên một số thuộc tập S. Tính xác suất để rút được số mà trong số đó chữ số đứng sau luôn lớn hơn hoặc
bằng chữ số đứng trước.
A.
2
7
. B.
3
32
. C.
11
64
. D.
3
16
.
Câu 28: Có tất cả bao nhiêu số nguyên dương m để phương trình
2
cos
cos x m x m
có nghiệm?
A. 2. B. 3. C. 1. D. 2.
Câu 29: Cho phương trình
06cossin352sin32cos xxxx
. Tính tổng giữa nghiệm dương
nhỏ nhất và nghiệm âm lớn nhất của phương trình .
A.
3
B.
2
. C.
2
3
. D.
4
.
Câu 30: :
Cho hàm số
f x
có đạo hàm trên
,
O
a
b
c
x
y
f x
Đề thi chọn HSG Toán 12 năm 2019
VnDoc xin giới thiệu tới bạn đọc Đề thi chọn học sinh giỏi lớp 12 chuyên Toán năm 2018 - 2019 cụm trường THPT Yên Dũng - Bắc Giang. Nội dung tài liệu gồm 40 câu hỏi trắc nghiệm, 3 câu hỏi bài tập, thời gian làm bài 120 phút. Mời các bạn học sinh tham khảo.
- Đề thi chọn học sinh giỏi Toán 12 năm 2018 - 2019 Sở GD&ĐT Đồng Nai
- Đề thi chọn học sinh giỏi Toán 12 năm 2018 - 2019 Sở GD&ĐT Vĩnh Phúc
- Đề thi chọn học sinh giỏi Toán 12 năm 2018 - 2019 Sở GD&ĐT Điện Biên
- Đề thi chọn học sinh giỏi cấp tỉnh Toán 12 năm 2018 - 2019 Sở GD&ĐT Lâm Đồng
- Đề thi chọn học sinh giỏi lớp 12 chuyên Toán năm 2018 - 2019 Sở GD&ĐT Đồng Nai
----------------------------
Trên đây VnDoc đã giới thiệu tới bạn đọc Đề thi chọn học sinh giỏi lớp 12 môn Toán năm 2018 - 2019 cụm trường THPT Yên Dũng - Bắc Giang. Để có kết quả cao hơn trong học tập, VnDoc xin giới thiệu tới các bạn học sinh tài liệu Thi thpt Quốc gia môn Toán, Thi thpt Quốc gia môn Hóa học, Thi thpt Quốc gia môn Vật Lý, Thi thpt Quốc gia môn Sinh học mà VnDoc tổng hợp và đăng tải.