Đề thi học kì 2 lớp 12 môn Toán năm 2018 - 2019 Sở GD&ĐT Bình Thuận
Đề kiểm tra HK2 Toán 12 có đáp án
SỞ GIÁO DỤC VÀ ĐÀO TẠO
BÌNH THUẬN
ĐỀ CHÍNH THỨC
(Đề này có 04 trang)
KIỂM TRA HỌC KỲ II LỚP 12
NĂM HỌC: 2018-2019
Môn: Toán
Thời gian làm bài: 90 phút (Không kể thời gian giao đề)
Họ và tên: ... . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Số báo danh: . . . . . . . . . . . . . . . . . . Lớp: . . . . . . . . . . . . . . . . . . Mã đề 491
Câu 1. Khẳng định nào sau đây đúng?
A. i
4
= −1. B. (1 − i)
2
là số thực. C. (1 + i)
2
= 2i. D. i
3
= i.
Câu 2. Trong không gian Oxyz, mặt phẳng (α) : 5x −7y − z + 2 = 0 nhận vectơ nào sau đây làm vectơ
pháp tuyến?
A.
−→
n
4
= (−5; −7; 1). B.
−→
n
3
= (5; −7; 1). C.
−→
n
1
= (5; 7; 1). D.
−→
n
2
= (−5; 7; 1).
Câu 3. Khẳng định nào sau đây sai?
A.
Z
kf(x) dx = k
Z
f(x) dx với k ∈ R\{0}. B.
Z
f(x) · g(x) dx =
Z
f(x) dx ·
Z
g(x) dx.
C.
Z
[f(x) + g(x)] dx =
Z
f(x) dx +
Z
g(x) dx. D.
Z
[f(x) − g(x)] dx =
Z
f(x) dx −
Z
g(x) dx.
Câu 4. Trong không gian Oxyz, mặt phẳng nào sau đây song song với trục Oy?
A. (δ) : 7x −4y + 6 = 0. B. (β) : 3x + 2z = 0. C. (γ) : y + 4z − 3 = 0. D. (α) : x − 3z + 4 = 0.
Câu 5.
Điểm M trong hình vẽ bên là điểm biểu diễn của số phức nào sau đây?
A. z = 1 − 3i. B. z = −1 + 3i. C. z = 3 + i. D. z = 3 − i.
O
x
y
x
−1
M
3
Câu 6. Trong không gian Oxyz, độ dài của vectơ
−→
u = (−3; 4; 0) bằng
A. 1. B.
√
5. C. 25. D. 5.
Câu 7. Cho hàm số y = f(x) liên tục trên đoạn [a; b]. Diện tích hình phẳng giới hạn bởi đồ thị của hàm
số y = f (x), trục hoành và hai đường thẳng x = a, x = b được tính theo công thức
A. S =
b
Z
a
f(x) dx. B. S = −
b
Z
a
f(x) dx. C. S =
b
Z
a
|f(x)| dx. D. S =
a
Z
b
|f(x)| dx.
Câu 8. Trong không gian Oxyz, cho đường thẳng d đi qua điểm M (0; −1; 4) và nhận vectơ
−→
u = (3; −1; 5)
làm vectơ chỉ phương. Hệ phương trình nào sau đây là phương trình tham số của d?
A.
x = 3t
y = 1 − t
z = 4 + 5t
. B.
x = 3
y = −1 − t
z = 5 + 4t
. C.
x = 3t
y = −1 − t
z = 4 + 5t
. D.
x = 3t
y = 1 − t
z = −4 + 5t
.
Câu 9. Số phức liên hợp của số phức z = 6 − 4i là
A. z = 4 + 6i. B. z = −6 + 4i. C. z = −6 − 4i. D. z = 6 + 4i.
Câu 10. Trong không gian Oxyz, cho đường thẳng ∆ :
x
−2
=
y
3
=
z − 3
1
. Vectơ nào sau đây là một
vectơ chỉ phương của ∆?
A.
−→
u
4
= (2; 3; 1). B.
−→
u
3
= (−2; 3; −1). C.
−→
u
1
= (−2; −3; 1). D.
−→
u
2
= (−2; 3; 1).
Câu 11. Trong không gian Oxyz, cho điểm A (2; −6; 8). Tâm mặt cầu đường kính OA có tọa độ là
A. (0; 0; 0). B. (2; −6; 8). C. (−1; 3; −4). D. (1; −3; 4).
Câu 12. Trong không gian Oxyz, vectơ
−→
u = −2
−→
i + 3
−→
j − 7
−→
k có tọa độ là
A. (−2; −3; −7). B. (−2; 3; −7). C. (2; 3; −7). D. (2; −3; 7).
Câu 13. Trong không gian Oxyz, vectơ nào sau đây vuông góc đồng thời với hai vectơ
−→
u = (1; −1; 0)
và
−→
v = (0; 3; 3)?
Trang 1/4 Mã đề 491
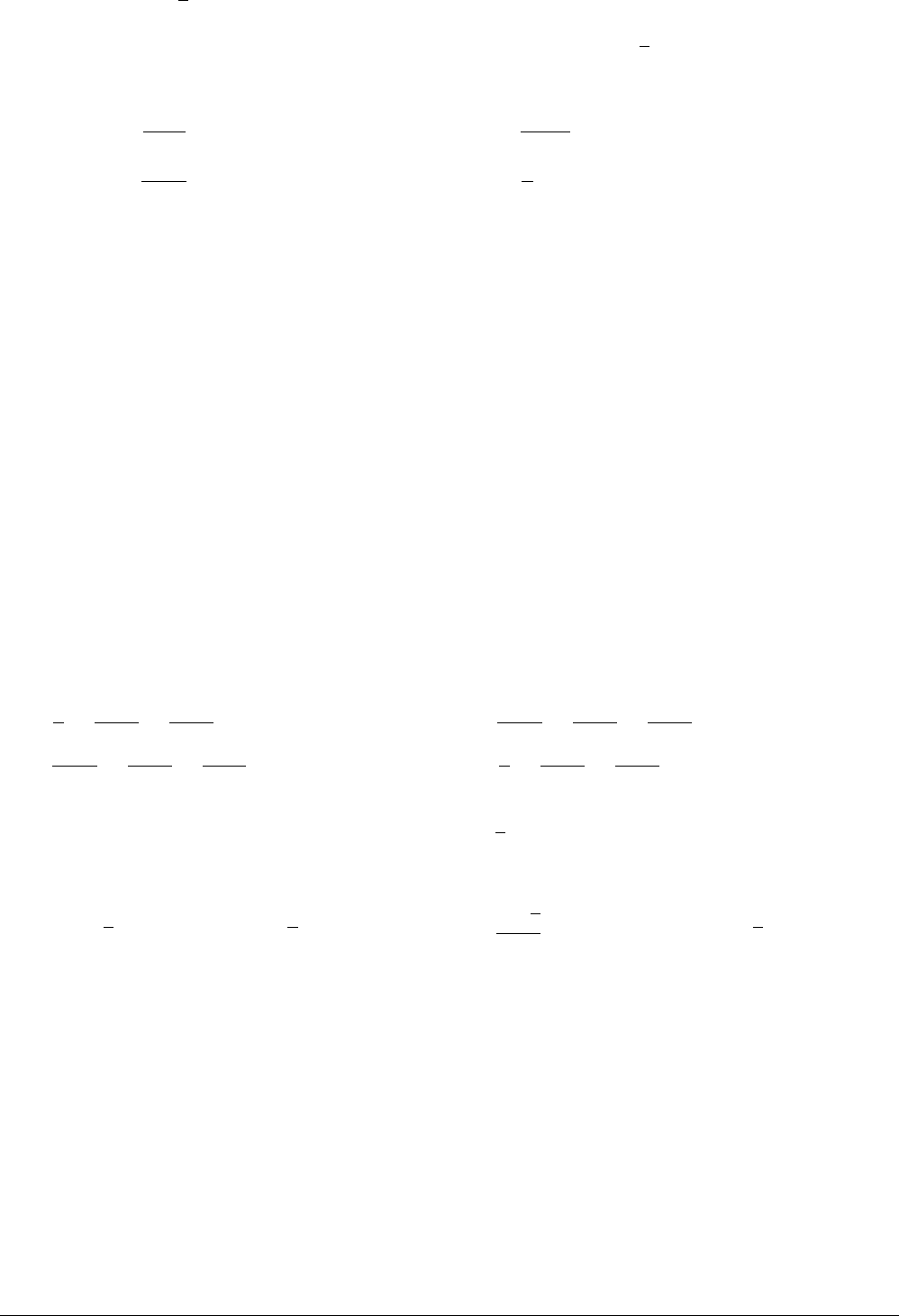
A.
−→
b = (3; 3; 0). B.
−→
c = (0; 1; −1). C.
−→
x = (0; 0; −3). D.
−→
a = (1; 1; −1).
Câu 14. Họ nguyên hàm của hàm số f(x) = cos 2x là
A.
Z
cos 2x dx =
1
2
sin 2x + C. B.
Z
cos 2x dx = sin 2x + C.
C.
Z
cos 2x dx = 2 sin 2x + C. D.
Z
cos 2x dx = −
1
2
sin 2x + C.
Câu 15. Khẳng định nào sau đây sai?
A.
Z
x
e
dx =
x
e+1
e + 1
+ C. B.
Z
1
cos
2
x
dx = tan x + C.
C.
Z
e
x
dx =
e
x+1
x + 1
+ C. D.
Z
1
x
dx = ln |x| + C.
Câu 16. Cho số phức z = 3 − 4i. Tính |z|.
A. |z| = 7. B. |z| = −1. C. |z| = 5. D. |z| = 1.
Câu 17. Trong không gian Oxyz, cho điểm M thỏa
−−→
OM = −4
−→
i + 5
−→
k . Khi đó, tọa độ của điểm M
là
A. (−4; 0; 5). B. (−4; 5; 0). C. (5; 0; −4). D. (4; 0; −5).
Câu 18. Số phức nào sau đây là số thuần ảo?
A. z = 7 + 3i. B. z = 5 + i. C. z = 7. D. z = 2i.
Câu 19. Trong mặt phẳng Oxy, tập hợp các điểm biểu diễn các số phức z thỏa mãn |z + i| = 2 là đường
tròn có phương trình
A. x
2
+ (y + 1)
2
= 2. B. x
2
+ (y + 1)
2
= 4. C. x
2
+ (y − 1)
2
= 4. D. (x − 1)
2
+ y
2
= 4.
Câu 20. Diện tích hình phẳng giới hạn bởi hai đường thẳng x = 0, x = π, đồ thị hàm số y = cos x và
trục Ox là
A. S = π
π
Z
0
|cos x|dx. B. S =
π
Z
0
cos
2
x dx. C. S =
π
Z
0
cos x dx. D. S =
π
Z
0
|cos x|dx.
Câu 21. Trong không gian Oxyz, hệ phương trình nào sau đây là phương trình chính tắc của đường
thẳng đi qua hai điểm A (−3; 3; 1) và B (0; 4; −2)?
A.
x
3
=
y + 4
−1
=
z − 2
−3
. B.
x + 3
3
=
y − 3
1
=
z − 1
−3
.
C.
x − 3
3
=
y + 3
1
=
z + 1
−3
. D.
x
3
=
y − 4
−1
=
z + 2
−3
.
Câu 22. Cho số phức z thỏa mãn
2i − i
2
z + 10i = 5. Khẳng định nào sau đây sai?
A. z có phần thực bằng −3. B. z = −3 + 4i.
C. z có phần ảo bằng 4. D. |z| = 5.
Câu 23. Cho số phức z. Đẳng thức nào sau đây sai?
A. |z| = |z|. B. z.z = |z|
2
. C.
z − z
i
là số thuần ảo. D. z + z là số thực.
Câu 24. Tìm hai số thực x, y thỏa mãn 2 + (5 − y)i = (x − 1) + 5i.
A.
(
x = −6
y = 3
. B.
(
x = −3
y = 0
. C.
(
x = 3
y = 0
. D.
(
x = 6
y = 3
.
Câu 25. Thể tích khối tròn xoay tạo thành khi quay hình phẳng giới hạn bởi các đường y = xe
x
, y = 0,
x = 0, x = 1 xung quanh trục Ox là
A. V = π
1
Z
0
x
2
e
2x
dx. B. V = π
1
Z
0
x
2
e
x
dx. C. V =
1
Z
0
x
2
e
2x
dx. D. V = π
1
Z
0
xe
x
dx.
Câu 26. Cho I =
4
Z
1
(mx + 668) dx (m là tham số thực). Tìm m để I = 2019.
A. m = −2. B. m = 2. C. m = 1. D. m = −1.
Trang 2/4 Mã đề 491
Câu 27. Trong không gian Oxyz, mặt cầu tâm I (−1; 0; 3) và tiếp xúc với mặt phẳng (α) : 4y−3z+19 = 0
có phương trình là
A. (x + 1)
2
+ y
2
+ (z − 3)
2
= 2. B. (x − 1)
2
+ y
2
+ (z + 3)
2
= 2.
C. (x − 1)
2
+ y
2
+ (z + 3)
2
= 4. D. (x + 1)
2
+ y
2
+ (z − 3)
2
= 4.
Câu 28. Thể tích của khối tròn xoay sinh ra khi cho hình phẳng giới hạn bởi parabol (P ): y = x
2
và
đường thẳng d : y = x quay quanh trục Ox bằng
A. π
1
Z
0
x
2
− x
2
dx. B. π
1
Z
0
x
2
− x
dx.
C. π
1
Z
0
x
2
dx + π
1
Z
0
x
4
dx. D. π
1
Z
0
x
2
dx − π
1
Z
0
x
4
dx.
Câu 29. Trong không gian Oxyz, cho tam giác ABC có A(1; 1; 1), B (−1; 0; 3), C (6; 8; −10). Gọi M, N, K
lần lượt là hình chiếu của trọng tâm tam giác ABC lên các trục Ox, Oy, Oz. Khi đó mặt phẳng (MN K)
có phương trình là
A.
x
2
+
y
3
+
z
−2
= 0. B.
x
2
+
y
3
+
z
−2
= 1. C.
x
2
+
y
−3
+
z
2
= 1. D.
x
2
+
y
−2
+
z
3
= 1.
Câu 30. Trong không gian Oxyz, cho tứ diện ABCD với A(3; 4; 1), B(2; −1; 2), C(5; −1; −1) và D(−1; 4; 0).
Viết phương trình mặt phẳng (P ) đi qua A, B và song song với CD.
A. (P ) : 2x + y + 7z + 2 = 0. B. (P ) : 2x + y + 7z + 17 = 0.
C. (P ) : 2x + y + 7z − 17 = 0. D. (P ) : 2x + y + 7z − 2 = 0.
Câu 31. Trong mặt phẳng Oxy, cho hình bình hành ABCD với A, B, C lần lượt là các điểm biểu diễn
các số phức 1 − 2i, 3 − i, 1 + 2i. Điểm D là điểm biểu diễn số phức z nào sau đây?
A. z = −1 + i. B. z = 5 − i. C. z = 3 + 3i. D. z = 3 − 5i.
Câu 32. Cho hai số phức z = −3 + 4i và w = 1 − 2i. Khi đó z − 3w bằng
A. 6 + 2i. B. −6 + 2i. C. −6 − 2i. D. 6 − 2i.
Câu 33. Thể tích V của khối tròn xoay được sinh ra khi quay hình phẳng giới hạn bởi các đường y =
√
3x,
y = 0 và hai đường thẳng x = 1, x = 2 quanh trục Ox là
A. V = 7π. B. V = 3π. C. V =
√
3π. D. V = π.
Câu 34. Cho số phức z thỏa z − z = 4i. Khi đó z có phần ảo bằng
A. 2. B. −4. C. 4. D. −2.
Câu 35. Tính tích phân I =
1
Z
0
2
x
dx.
A. I =
2
ln 2
. B. I =
3
2
. C. I = 1. D. I =
1
ln 2
.
Câu 36. Thể tích khối tròn xoay sinh ra khi cho hình phẳng giới hạn bởi các đường y = sin x; y = 0;
x = 0; x = 2π quay quanh trục Ox là
A. V =
π
4
. B. V =
π
2
. C. V =
π
2
2
. D. V = π
2
.
Câu 37. Cho hai số phức z
1
= x − 2i và z
2
= 3 + yi, với x, y ∈ R. Khi đó, z
1
.z
2
là số thực khi và chỉ
khi
A. xy = −3. B. xy = 3. C. xy = 6. D. xy = −6.
Câu 38. Biết
Z
x sin 2x dx = ax cos 2x + b sin 2x + C với a, b là các số hữu tỉ. Tính tích ab.
A. ab = −
1
4
. B. ab = −
1
8
. C. ab =
1
4
. D. ab =
1
8
.
Câu 39. Khẳng định nào sau đây đúng?
A.
Z
ln x
x
dx = 2 ln x + C. B.
Z
ln x
x
dx = ln
2
x + C.
C.
Z
ln x
x
dx =
1
2
ln
2
x + C. D.
Z
ln x
x
dx = 2 ln
2
x + C.
Trang 3/4 Mã đề 491
Đề thi học kì 2 Toán 12
VnDoc xin giới thiệu tới bạn đọc Đề thi học kì 2 lớp 12 môn Toán năm 2018 - 2019 Sở GD&ĐT Bình Thuận. Nội dung tài liệu gồm 50 câu hỏi trắc nghiệm, thời gian làm bài 90 phút, đề thi có đáp án. Mời các bạn học sinh tham khảo.
- Đề thi học kì 2 lớp 12 môn Toán năm 2018 - 2019 Sở GD&ĐT Đồng Tháp
- Đề thi học kì 2 lớp 12 môn Toán năm 2018 - 2019 Sở GD&ĐT Bạc Liêu
- Đề thi giữa học kì 2 lớp 12 môn Toán năm 2018 - 2019 trường THPT C Nghĩa Hưng - Nam Định
- Đề thi giữa học kì 2 lớp 12 môn Toán năm 2018 - 2019 trường THPT Gia Định - TP. HCM
- Đề thi giữa học kì 2 lớp 12 môn Toán năm 2018 - 2019 trường THPT Nhân Chính - Hà Nội
- Đề thi giữa học kì 2 lớp 12 môn Toán năm 2018 - 2019 trường THPT Nguyễn Chí Thanh - TP. HCM
Trên đây VnDoc đã giới thiệu tới bạn đọc Đề thi học kì 2 lớp 12 môn Toán năm 2018 - 2019 Sở GD&ĐT Bình Thuận. Để có kết quả cao hơn trong học tập, VnDoc xin giới thiệu tới các bạn học sinh tài liệu Giải bài tập Toán lớp 12, Giải bài tập Hóa học lớp 12, Giải bài tập Vật Lí 12, Tài liệu học tập lớp 12 mà VnDoc tổng hợp và đăng tải.






