VnDoc.com

Đề thi học sinh giỏi cấp tỉnh môn Toán lớp 11 năm học 2018 - 2019 Sở GD&ĐT Thanh Hóa

Đề thi HSG Toán 11 có đáp án

1 265

VnDoc - Tải tài liệu, văn bản pháp luật, biểu mẫu miễn phí

SỞ GIÁO DỤC VÀ ĐÀO TẠO

THANH HÓA

ĐỀ THI THỬ SỐ 1

KÌ THI HỌC SINH GIỎI CẤP TỈNH

Năm học: 2018 - 2019

Môn thi: TOÁN - Lớp 11 THPT

Thời gian: 180 phút (không kể thời gian giao đề)

Đề thi có 01 trang, gồm 05 câu

Câu I (4,0 điểm)

1. Cho hàm số

2

2 3y x m x m  

(*). Lập bảng biến thiên và vẽ đồ thị của hàm số (*) khi

1.m 

Tìm

m để đường thẳng

2 3y x  

cắt đồ thị các hàm số (*) tại hai điểm phân biệt cùng nằm bên phải trục tung.

2. Giải bất phương trình

(2 1)

1

2 (2 ) 1 1

x x

x x x x





    

.

Câu II (4,0 điểm)

1. Giải phương trình

3 cos sin 1

3tan2 2sin 2 2

2 cos sin cos2

x x

x x x



   



   

   



   

2. Giải hệ phương trình

 

2

1 1

2

3 3

2 9 4 3 19 3

x y

x y y x

x y x y



 

  



 



 

 



 



     





Câu III (4,0 điểm)

1. Cho

, ,a b c

là các số thực dương thoả mãn

1abc 

. Chứng minh bất đẳng thức

3 3 3

2 2 2 2 2 2

9

2

ab bc ca

a b c

a b b c c a

     

  

.

2. Cho

 

2

1 1f n n n   

. Xét dãy số

 

:

n

u

    

     

1 3 ... 2 1

2 4 ... 2

n

f f n

u

f f f n





. Tính

lim

n

n u

.

Câu IV (4,0 điểm)

1. Từ tập

 

0;1;2;3;4;5;6A 

có bao nhiêu số tự nhiên có năm chữ số chia hết cho

9

.

2. Trong mặt phẳng với hệ tọa độ

,Oxy

cho tứ giác

MNPQ

nội tiếp đường tròn

( )

C

có tâm

· ·

·

0

, , 90 .I MQP MNP MIP> =

Tiếp tuyến của đường tròn

( )

C

tại

Q

cắt các tiếp tuyến tại

,M P

lần lượt tại

, .E F

Phương trình đường thẳng

: 7 8 0,I F x y- + =

( )

2;4 ,N -

11

1; .

3

E

÷

ç

÷

ç

÷

ç

÷

ç

Tìm tọa độ giao điểm

A

của các

tiếp tuyến với đường tròn

( )

C

tại

M

và tại

.P

Câu V (4,0 điểm)

1. Cho hình chóp

.S ABC

có

  AB BC CA a

,

3  SA SB SC a

,

M

là điểm bất kì trong không gian.

Gọi

d

là tổng khoảng cách từ

M

đến tất cả các đường thẳng

AB

,

BC

,

CA

,

SA

,

SB

,

SC

. Tìm giá trị nhỏ

nhất của

d

Số báo danh

……………………............

VnDoc - Tải tài liệu, văn bản pháp luật, biểu mẫu miễn phí

2. Cho hình chóp tam giác đều

.S ABC

cạnh đáy

a

, đường cao

2SO a

. Gọi

M

là điểm thuộc đường cao

'

AA

của tam giác

ABC

. Xét mặt phẳng

 

P

đi qua

M

và vuông góc với

'

AA

. Đặt

AM x

3 3

3 2

a a

x

 

 

 

 

. Tìm

x

để thiết diện của hình chóp khi cắt bởi mặt phẳng

 

P

có diện tích lớn nhất.

…………………..Hết………………….

ĐÁP ÁN - THANG ĐIỂM

Câu

NỘI DUNG

Điểm

I

1. Cho hàm số

2

2 3y x mx m  

(*)

Lập bảng biến thiên và vẽ đồ thị của hàm số (*) khi

1.m 

Tìm m để đường thẳng

2 3y x  

cắt đồ thị các hàm số (*) tại hai điểm phân biệt cùng nằm bên phải trục

tung.

2.0

4,0

điểm

Lập bảng biến thiên

0.50

Vẽ đồ thị

0.50

Yêu cầu bài toán



Phương trình sau có hai nghiệm dương phân biệt

2 2

2 3 2 3 2( 1) 3 3 0x mx m x x m x m          

' 0

3( 1) 0

2( 1) 0

m

 





   





  



0.50

1

' 0

4

m

 



  



 



Kết hợp nghiệm, kết luận

4m  

0.50

2. Giải bất phương trình

(2 1)

1

2 (2 ) 1 1

x x

x x x x





    

.

2.0

Điều kiện:

0 1.x 

Ta có:

2

2 (2 ) 1 1 2 2 1 . 1 ( 1 )x x x x x x x x x           

2( 1 ) 1 ( 1 ) ( 1 )(2 1 ) 0, 0;1 .x x x x x x x x x                

 

0.50

( ) (2 1) ( 1 ) (2 1 )x x x x x         

2 2

( ) ( 1 ) ( 1 ) (2 1 )x x x x x x

 

         

 

0.50

( 1 ) ( 1 ) ( 1 ) (2 1 )x x x x x x x x            

 

( 1 ) 2 1 , do : 1 0, 0;1x x x x x x x            

 

0.50

(1 ) 2 1 2 1 (1 ) :x x x x x x x          

luôn đúng

0;1 .x   

 

Kết luận: Tập nghiệm cần tìm của bất phương trình là

0;1 .x   

 

0.50

II

1. Giải phương trình

3 cos sin 1

3tan2 2sin 2 2

2 cos sin cos2

x x

x x x



   



   

   



   

2.0

4,0

điểm

Điều kiện:

 

cos2 0

4 2

x x k k

 

     

(*).

VnDoc - Tải tài liệu, văn bản pháp luật, biểu mẫu miễn phí

Với điều kiện trên phương trình đã cho tương đương với:

 



       



2

2 cos sin

sin2 1

3 2cos2 3sin2 2cos 2 2 cos sin 1

cos2 cos sin cos2

x x

x

x x x x x

x x x x

0.50

 



 



          









2 2

sin2 1

3sin2 2 1 sin 2 2 1 sin2 1 2sin 2 sin2 1 0

1

sin2

2

x

x x x x x

x

0.50

Với



    sin2 1

4

x x k

0.50

Với

 





 



  



 







1

12

sin2

2

5

12

x k

Kết hợp với điều kiện (*) ta được nghiệm của phương trình đã cho là:

12

x k



 

và

 

5

12

x k k



   

0.50

2. Giải hệ phương trình

 

2

1 1

2

3 3

2 9 4 3 19 3

x y

x y y x

x y x y



 

  



 



 

 



 



     





2.0

Điều kiện

19

0, 0

3

0

x y



  







 



Từ

 

1

: s dụng bất đẳng thức G ta có

1

3 2 3

3

x x x y x x y

x y x y x y x y

x y

 

 

   

 

   



 

và

1 2 1 1 2

2 3 2 2 3

3

y

y y

x y x y

x y

 

   

 

 



 

, cộng hai kết quả trên ta được

0.50

1 3

2 2

3

x y

x

x y



 

 

 



 

, tương tự ta cⴧng có

1 3

2 2

3

x y

y

x y

y x



 

 

 



 

,

suy ra

 

1 1

1 1 1

3 2

2

3 3

x y

VT x y VP

x y

x y y x

 



      

 



 

 

ấu bằng y ra khi và ch khi

 

3x y

0.50

Thế vào phương trình

 

2

ta được pt:

2

2 9 4 3 19 3x x x x     

 

4

Giải pt

 

   

2

4 3 2 4 3 3 5 3 19 3 13x x x x x x

   

          

   

0.50

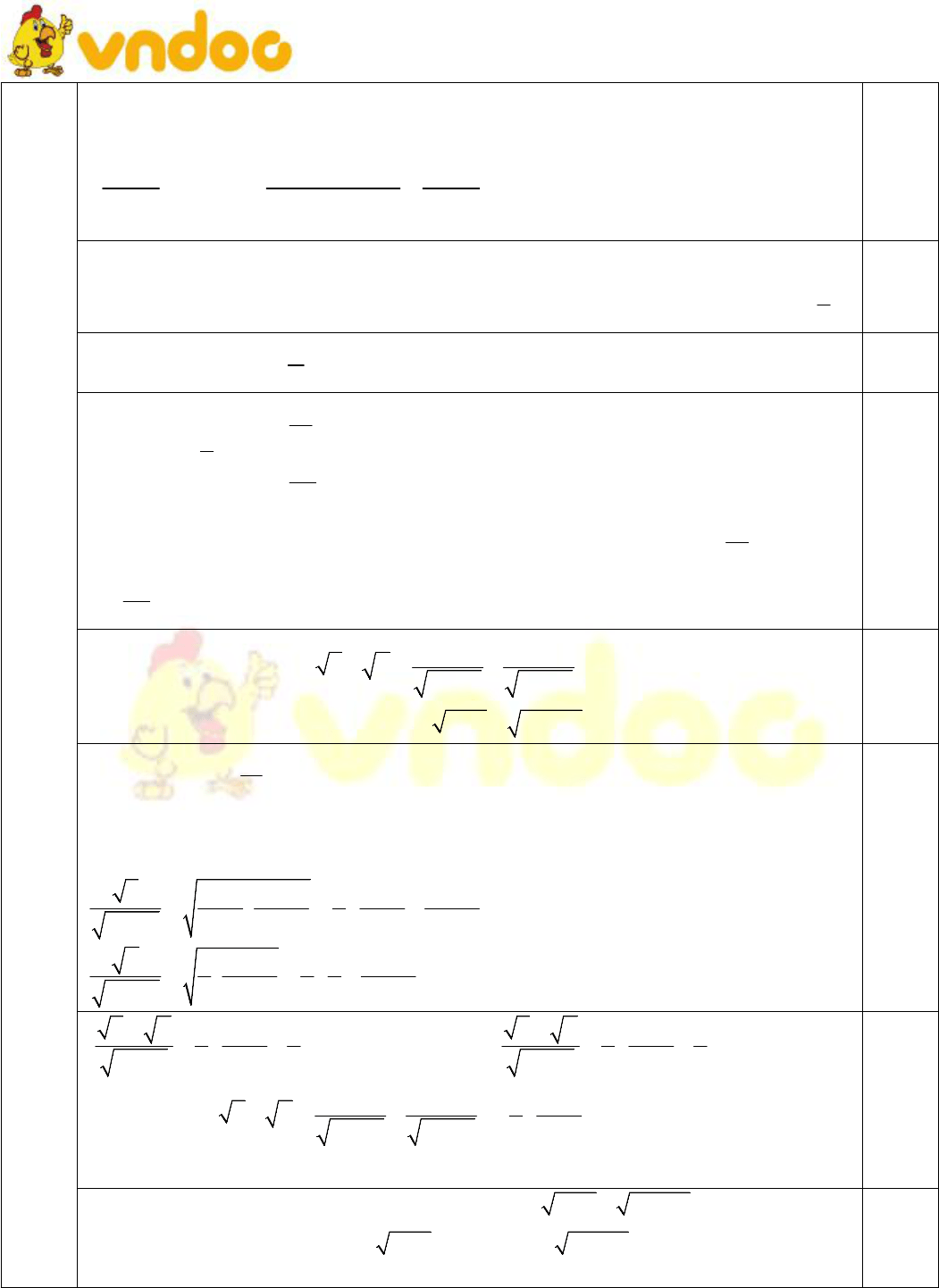
Đề thi chọn học sinh giỏi môn Toán lớp 11

VnDoc xin giới thiệu tới bạn đọc Đề thi học sinh giỏi cấp tỉnh lớp 11 môn Toán năm 2018 - 2019 Sở GD&ĐT Thanh Hóa. Nội dung tài liệu bao gồm 5 câu hỏi lớn có đáp án và lời giải chi tiết rõ ràng, giúp các em học sinh ôn tập, đồng thời cũng là tài liệu hữu ích cho thầy cô tham khảo ôn luyện cho đội tuyển thi học sinh giỏi.

Đề thi học sinh giỏi cấp tỉnh môn Toán lớp 11 năm học 2018 - 2019 Sở GD&ĐT Thanh Hóa nằm trong bộ đề ôn thi học sinh giỏi lớp 11 được VnDoc.com sưu tầm và tuyển chọn từ những đề thi của các trường THPT, các Sở GD&ĐT trên khắp cả nước. Các em học sinh hãy tham khảo và luyện tập để làm quen với nhiều dạng đề thi khác nhau, từ đó có sự chuẩn bị tốt nhất cho kì thi học sinh giỏi sắp tới của mình.

Trên đây VnDoc đã giới thiệu tới các bạn Đề thi học sinh giỏi cấp tỉnh môn Toán lớp 11 năm học 2018 - 2019 Sở GD&ĐT Thanh Hóa. Để có kết quả cao hơn trong học tập, VnDoc mời các bạn học sinh tham khảo Giải bài tập Sinh học lớp 11, Giải bài tập Vật lý lớp 11, Giải bài tập Hóa học lớp 11, Giải bài tập Toán lớp 11, Tài liệu học tập lớp 11 mà VnDoc tổng hợp và đăng tải.