Đề thi thử THPT Quốc gia năm 2015 môn Toán trường THPT Trần Thị Tâm, Quảng Trị
Đề thi thử THPT Quốc gia môn Toán
Đề thi thử THPT Quốc gia năm 2015 môn Toán trường THPT Trần Thị Tâm, Quảng Trị được VnDoc.com sưu tầm và đăng tải là tài liệu ôn thi THPT Quốc gia môn Toán có đáp án hay dành cho các bạn tham khảo, luyện đề thi chuẩn bị cho các kì thi quan trọng sắp tới. Mời các bạn tham khảo.
Tổng hợp các đề thi thử THPT Quốc gia môn Toán tháng 4 năm 2015
Đề thi thử THPT Quốc gia môn Toán lần 2 năm 2015 trường THPT Chuyên Long An, Long An
Đề thi thử THPT Quốc gia môn Toán lần 1 năm 2015 trường THPT Trần Đại Nghĩa
| SỞ GD&ĐT QUẢNG TRỊ TRƯỜNG THPT TRẦN THỊ TÂM | ĐỀ THI THỬ - KỲ THI THPT QUỐC GIA NĂM 2015 MÔN: TOÁN Thời gian làm bài: 180 phút (không kể thời gian giao đề) |
Câu 1: (2,0 điểm) Cho hàm số y = x3 + 3x2 + 1 (C).
a) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số đã cho
b) Viết phương trình tiếp tuyến của đồ thị (C), biết tiếp điểm có tung độ y = 1.
Câu 2: (1,0 điểm)
| a) Giải phương trình: |
b) Cho số phức z thỏa mãn hệ thức: ![]() . Tính mô đun của số phức z.
. Tính mô đun của số phức z.
Câu 3: (0.5 điểm) Giải phương trình: log2(3x + 2) = 6 + log1/2(5x - 2).
| Câu 4: (1 điểm) Giải hệ phương trình: | 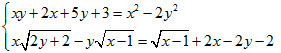 |
| Câu 5: (1 điểm) Tính tích phân: | 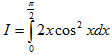 |
Câu 6: (1 điểm) Cho hình chóp S.ABC có đáy là tam giác ABC đều cạnh a, SA = a. Chân đường vuông góc hạ từ S xuống mặt phẳng (ABC) là trung điểm cạnh BC. Tính thể tích chóp S.ABC và khoảng cách giữa hai đường thẳng BC và SA theo a
Câu 7: (1 điểm) Trong không gian với hệ tọa độ Oxyz, cho điểm M(2; 1; 0) và đường thẳng d có phương trình: (x - 1)/2 = (y + 1)/1 = z/-1.
a) Tìm tọa độ hình chiếu vuông góc của điểm M lên đường thẳng d.
b) Viết phương trình chính tắc của đường thẳng đi qua điểm M, cắt và vuông góc với đường thẳng d.
Câu 8: (1 điểm) Trong mặt phẳng oxy cho tam giác ABC có phương trình cạnh BC là x - 2y + 3 = 0, trọng tâm G(4; 1) và diện tích bằng 15. Điểm E(3; -2) là điểm thuộc đường cao của tam giác ABC hạ từ đỉnh A. Tìm tọa độ các điểm A, B, C.
Câu 9: (0.5 điểm) Một hộp có 5 viên bi đỏ, 3 viên bi vàng và 4 viên bi xanh. Lấy ngẫu nhiên 4 viên bi từ hộp. Tính xác suất để 4 viên bi lấy được có số bi đỏ lớn hơn số bi vàng.
Câu 10: (1 điểm) Cho các số thực dương thỏa mãn: 5(x2 + y2 + z2) = 9(xy + 2yz + zx).
Tìm giá trị lớn nhất của biểu thức
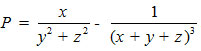
Đáp án đề thi thử THPT Quốc gia môn Toán
Câu 1: (2,0 điểm)
a) (1,0 điểm)
+ Tập xác định: D = R.
+ Giới hạn:
| lim y = -∞ | lim y = +∞ | y' = 3x2 + 6x |
| x→-∞ | x→+∞ |
+ Sự biến thiên:
Chiều biến thiên: y' = 0 ↔ x = 0 hay x = -2.
Suy ra hàm số nghịch biến trên khoảng (-2;0) và đồng biến trên các khoảng (-∞;-2), (0; +∞)
Cực trị: Hàm số đạt cực đại tại x = -2; yCĐ = 5, đạt cực tiểu tại x = 0; yCT = 1.
Bảng biến thiên:
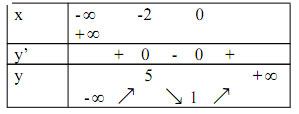
+ Đồ thị (C)
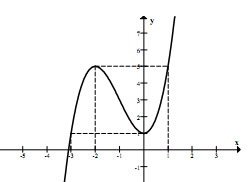
b) (1,0 điểm)
Hoành độ của tiếp điểm là nghiệm của phương trình x3 + 3x2 + 1 = 1. Suy ra x0 = 0; x0 = -3
Suy ra hệ số góc của tiếp tuyến là: y'(0) = 0; y'(-3) = 9.
Phương trình tiếp tuyến của (C) tại điểm (0;1) là: y = 1
Phương trình tiếp tuyến của (C) tại điểm (-3;1) là: y = 9x + 28
Câu 2: (1,0 điểm)
a) (0,5 điểm)
Điều kiện: cosx ≠ 1 ↔ x ≠ k2π, k ∈ Z.
Với điều kiện trên phương trình đã cho tương đương:
1 - cosx(2cosx + 1) - √2sinx = 1 - cosx ↔ 2sin2x - √2sinx - 2 = 0.
↔ sinx = -√2/2 ↔ x = -π/4 + kπ, k ∈ Z; x = 5π/4 + kπ, k ∈ Z (thỏa điều kiện)
b) (0,5 điểm)
Gọi z = x+yi. Phương trình đã cho trở thành:
(1 + 2i)(x + yi) + (2 - 3i)(x - yi) = -2 - 2i
↔ (x - 2y) + (2x + y)i + (2x - 3y) + (-3x - 2y)i = -2 - 2i
↔ (3x - 5y) + (-x - y)i = -2 - 2i
| ↔ { | 3x - 5y = -2 | ↔ { | x = 1 |
| -x - y = -2 | y = 1 |
Do đó |z| = √(12 + 12) = √2.






