Đề thi thử vào lớp 10 lần 1 môn Toán năm học 2015-2016 trường THCS Lý Tự Trọng, Ninh Bình
Đề thi thử vào lớp 10 môn Toán
Đề thi thử vào lớp 10 lần 1 môn Toán năm học 2015-2016 trường THCS Lý Tự Trọng, Ninh Bình có đáp án kèm theo là tài liệu ôn thi vào lớp 10 môn toán hay. Tài liệu này giúp các bạn ôn tập và củng cố lại kiến thức, nhằm đạt kết quả tốt trong kì thi chuyển cấp.
10 đề luyện thi vào lớp 10 môn Tiếng Anh
Đề thi thử vào lớp 10 môn Toán thành phố Hà Nội năm học 2015-2016
PHÒNG GDĐT TP. NINH BÌNH | ĐỀ THI THỬ TUYỂN SINH LỚP 10 THPT LẦN 1 |
Câu 1 (2,0 điểm)
Thực hiện các phép tính sau:
![]()
Câu 2 (2,5 điểm)
1) Cho hàm số bậc nhất y = (m - 2)x + m + 3 (d)
a) Tìm m để hàm số đồng biến.
b) Tìm m để đồ thị hàm số (d) song song với đồ thị hàm số y = 2x + 7.
2) Cho phương trình x2 - (2m - 1)x + m + 2, (x là ẩn, m là tham số).
a) Giải phương trình đã cho với m = 1.
b) Tìm tất cả các giá trị của tham số m để phương trình đã cho có hai nghiệm x1, x2 thỏa mãn: x12 + x22 = 15.
Câu 3 (2,0 điểm)
Nếu hai vòi nước cùng chảy vào một bể không có nước thì sau 12 giờ đầy bể. Sau khi hai vòi cùng chảy 8 giờ thì người ta khóa vòi thứ nhất, còn vòi thứ hai tiếp tục chảy. Do tăng công suất vòi thứ hai lên gấp đôi nên vòi thứ hai đã chảy đầy phần còn lại của bể trong 3 giờ rưỡi. Hỏi nếu mỗi vòi chảy một mình với công suất bình thường thì sau bao lâu đầy bể.
Câu 4 (3,0 điểm)
Cho nửa đường tròn tâm O đường kính AB. Một điểm C cố định thuộc đoạn thẳng AO (C khác A và C khác O). Đường thẳng đi qua điểm C và vuông góc với AO cắt nửa đường tròn đã cho tại D. Trên cung BD lấy điểm M (M khác B và M khác D). Tiếp tuyến của nửa đường tròn đã cho tại M cắt đường thẳng CD tại E. Gọi F là giao điểm của AM và CD.
1) Chứng minh rằng tứ giác BCFM là tứ giác nội tiếp đường tròn.
2) Chứng minh: EM = EF
3) Gọi I là tâm đường tròn ngoại tiếp tam giác FDM. Chứng minh ba điểm D, I, B thẳng hàng; từ đó suy ra góc ABI có số đo không đổi khi M thay đổi trên cung BD.
Câu 5 (0,5 điểm)
Cho các số thực dương x, y thoả mãn x + y = 2. Chứng minh rằng x/(1 + y2) + y/(1 + x2) ≥ 1.
Đáp án đề thi thử vào lớp 10 môn Toán
Câu 1 (2,0 điểm)
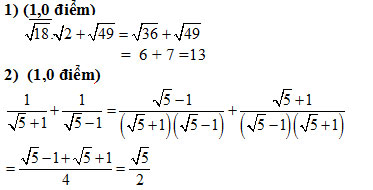
Câu 2 (2,5 điểm)
1) (1,0 điểm)
a) Hàm số bậc nhất y = (m - 2)x + m + 3 (d)
Hàm số đồng biến ↔ m – 2 > 0 ↔ m > 2
b) Đồ thị hàm số y = (m - 2)x + m + 3 (d) song song với đồ thị hàm số y = 2x +7 ↔ m - 2 = 2 và m + 3 ≠ 7 ↔ m = 4 và m ≠ 4 (vô lí)
Vậy không có m thỏa mãn đề bài.
2) (1,5 điểm)
Phương trình x2 - (2m - 1)x + m + 2 = 0
a) Khi m = 1 phương trình có dạng x2 - x - 1 = 0
Δ = (-1)2 - 4.1. (-1) = 5 > 0
Phương trình có hai nghiệm phân biệt: x1 = (1 - √5)/2 và x2 = (1 + √5)/2.








