Đề thi tuyển sinh vào lớp 10 môn Toán Sở GD&ĐT Thanh Hóa năm học 2018 - 2019
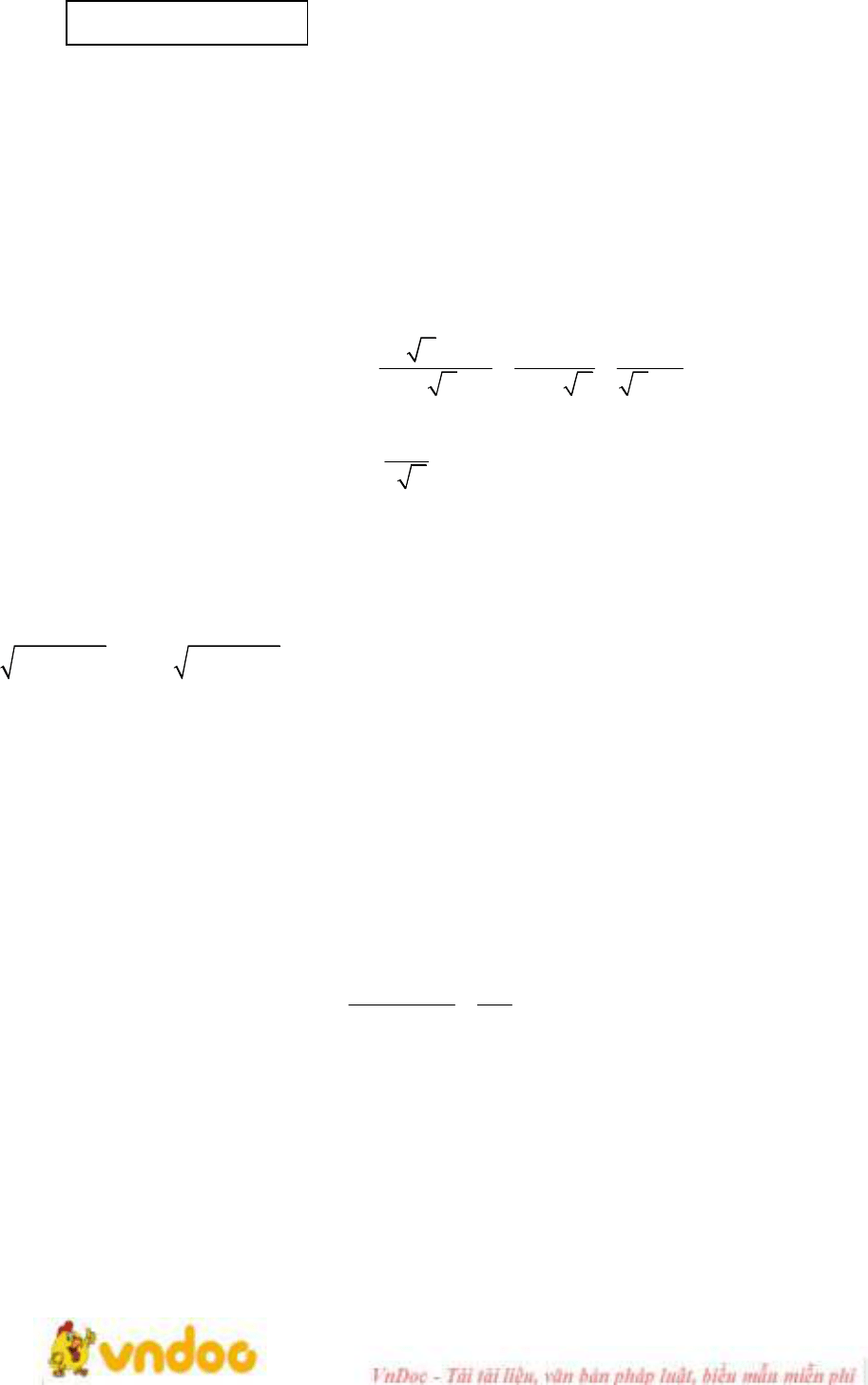
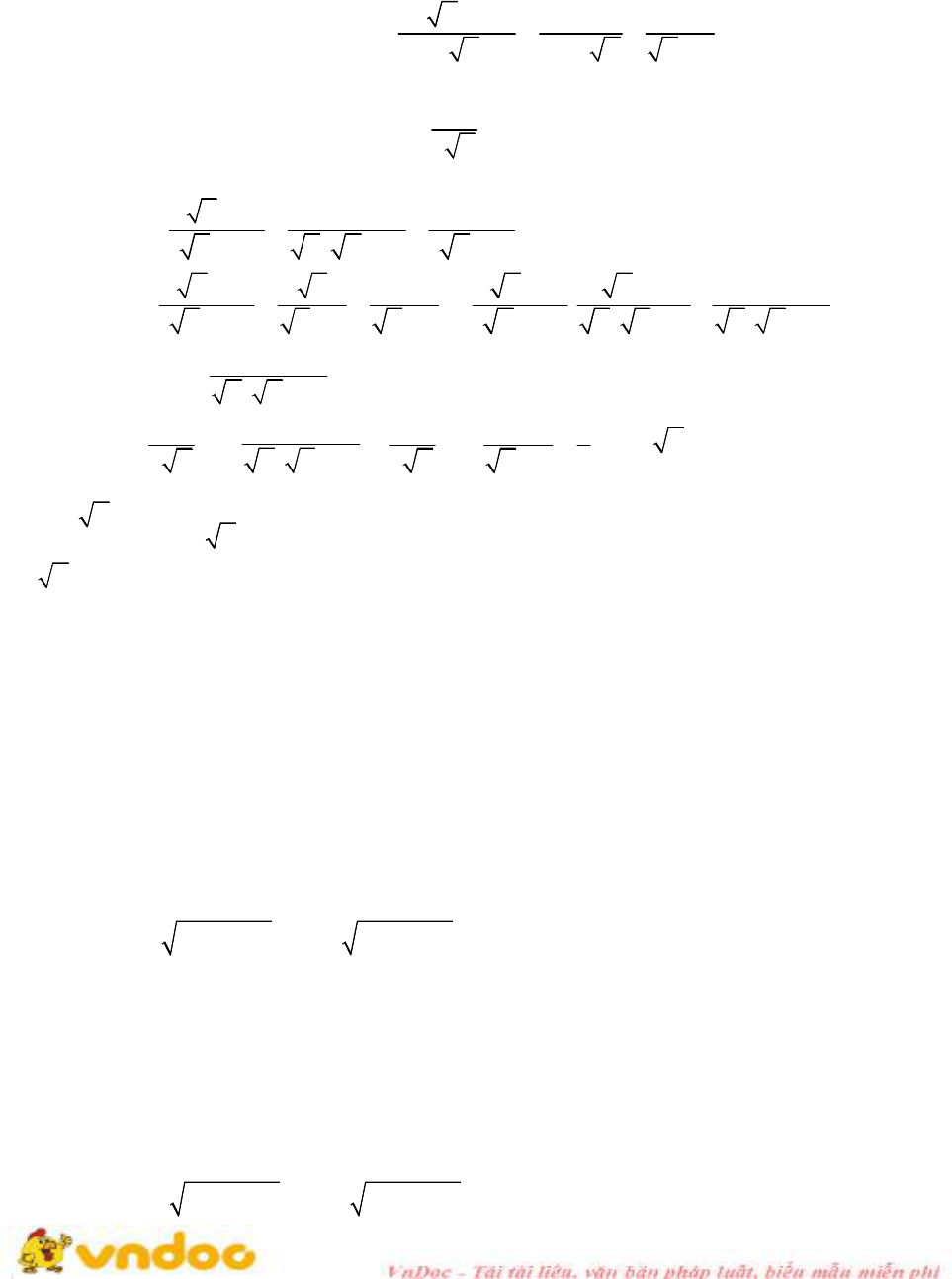
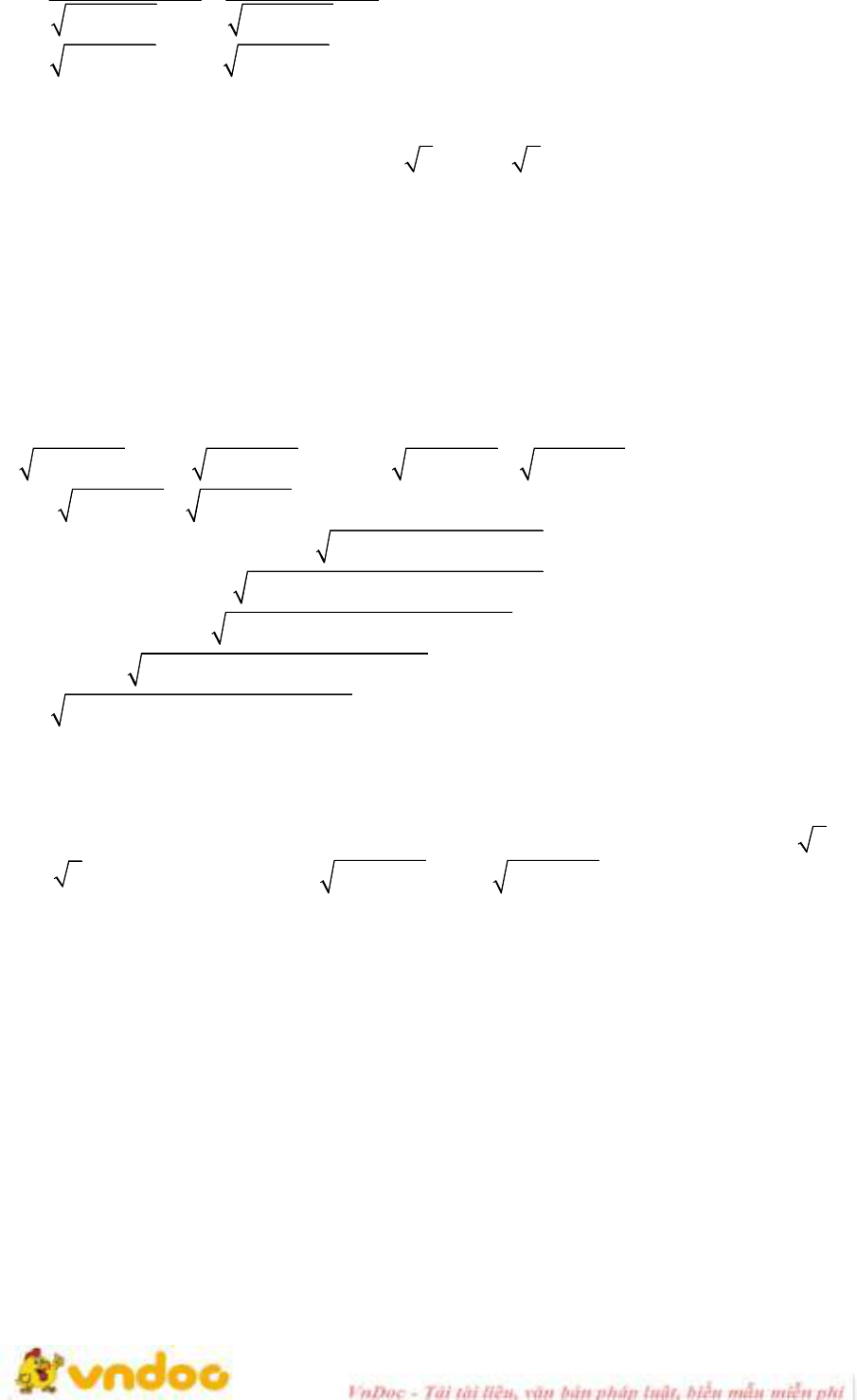
Đề thi tuyển sinh vào lớp 10 môn Toán Sở GD&ĐT Thanh Hóa
Đề thi tuyển sinh vào lớp 10 môn Toán Sở GD&ĐT Thanh Hóa năm học 2018 - 2019 có đáp án được VnDoc sưu tầm và đăng tải nhằm giúp các bạn học sinh có thêm nhiều tài liệu ôn thi vào lớp 10 môn Toán để tham khảo chuẩn bị tốt cho kì thi tuyển sinh sắp tới đây đạt kết quả cao. Mời các bạn cùng tham khảo.
Đề thi tuyển sinh vào lớp 10 THPT môn Ngữ văn Sở GD&ĐT Hưng Yên năm học 2018 - 2019
Đề thi tuyển sinh vào lớp 10 THPT môn Toán Sở GD&ĐT Thành Phố Hồ Chí Minh năm học 2018 - 2019
Đề thi tuyển sinh vào lớp 10 THPT môn Toán Sở GD&ĐT An Giang năm học 2018 - 2019
Mời các bạn tham khảo tài liệu liên quan
Đề thi tuyển sinh vào lớp 10 môn Ngữ văn Sở GD&ĐT Cần Thơ năm học 2018 - 2019
Đáp án đề thi tuyển sinh vào lớp 10 THPT môn Ngữ văn Sở GD&ĐT Hà Nội năm 2018
Đáp án đề thi vào lớp 10 môn Toán Sở GD&ĐT Hà Nội năm học 2018 - 2019
Đề thi tuyển sinh vào lớp 10 môn Ngữ văn Sở GD&ĐT Thanh Hóa năm học 2018 - 2019






