Đề thi tuyển sinh vào lớp 10 THPT môn Toán (Chuyên) trường THPT Chuyên Lê Qúy Đôn, Bà Rịa - Vũng Tàu năm 2016 - 2017
Đề thi tuyển sinh vào lớp 10 THPT môn Toán
Đề thi tuyển sinh vào lớp 10 THPT môn Toán (Chuyên) trường THPT Chuyên Lê Qúy Đôn, Bà Rịa - Vũng Tàu năm 2016 - 2017 được VnDoc sưu tầm và đăng tải nhằm giúp các em học sinh có thêm nhiều tài liệu ôn thi vào lớp 10 môn Toán để tham khảo chuẩn bị tốt cho kì thi tuyển sinh sắp tới đây đạt kết quả cao. Mời các em cùng tham khảo.
Đề thi tuyển sinh vào lớp 10 THPT môn Vật lý sở GD&ĐT Hưng Yên năm 2016 - 2017
Đề thi tuyển sinh vào lớp 10 môn Toán năm học 2015-2016 tỉnh Bà Rịa - Vũng Tàu
Đề thi tuyển sinh vào lớp 10 THPT chuyên môn Ngữ văn trường Đại học Sư Phạm Hà Nội năm 2016 - 2017
Đề thi tuyển sinh vào lớp 10 THPT chuyên môn Toán trường Đại học Sư Phạm Hà Nội năm 2016 - 2017
| SỞ GIÁO DỤC VÀ ĐÀO TẠO TỈNH BÀ RỊA – VŨNG TÀU THPT Chuyên Lê Qúy Đôn | KỲ THI TUYỂN SINH LỚP 10 THPT CHUYÊN NĂM HỌC 2016 – 2017 Môn: TOÁN (Chuyên) Thời gian làm bài: 150 phút Ngày thi: 31/5/2016 |
ĐỀ CHÍNH THỨC
Câu 1 (3,0 điểm).
a) Rút gọn biểu thức với ![]()
b) Giải phương trình ![]()
c) Giải hệ phương trình 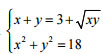
Câu 2 (2,0 điểm).
a) Tìm tất cả các cặp số nguyên tố (p; q) thỏa mãn p2 - 5q2 = 4
b) Cho đa thức ƒ(x) = x2 + bx + c. Biết b, c là các hệ số dương và ƒ(x) có nghiệm. Chứng minh ƒ(2) ≥ 93√c.
Câu 3 (1,0 điểm).
Cho x, y, z là 3 số dương thỏa mãn x2 + y2 + z2 = 3xyz. Chứng minh: ![]()
Câu 4 (3,0 điểm).
Cho hai đường tròn (O) và (0') cắt nhau tại A và B (OO' > R > R'). Trên nửa mặt phẳng bờ là OO' có chứa điểm A, kẻ tiếp tuyến chung MN của hai đường tròn trên (với M thuộc (O) và N thuộc (O')). Biết BM cắt (O') tại điểm E nằm trong đường tròn (O) và đường thẳng AB cắt MN tại I.
a) Chứng minh ∠MAN + ∠MBN = 180o và I là trung điểm của MN
b) Qua B, kẻ đường thẳng (d) song song với MN, (d) cắt (O) tại C và cắt (O') tại D (với C, D khác B). Gọi P, Q lần lượt là trung điểm của CD và EM. Chứng minh tam giác AME đồng dạng với tam giác ACD và các điểm A, B, P, Q cùng thuộc một đường tròn.
c) Chứng minh tam giác BIP cân.
Câu 5 (1,0 điểm).
Cho tam giác ABC có ba góc nhọn và H là trực tâm.
Chứng minh ![]() .
.






