Đề thi tuyển sinh vào lớp 10 THPT môn Toán tỉnh Bắc Giang năm 2015 - 2016
Đề thi vào lớp 10 THPT môn Toán tỉnh Bắc Giang
Đề thi tuyển sinh vào lớp 10 THPT môn Toán tỉnh Bắc Giang năm 2015 - 2016 gồm 5 câu hỏi có đáp án đi kèm, đây là đề thi luyện tập chuẩn bị hữu ích dành cho các bạn học sinh lớp 9, giúp các bạn có thể ôn tập và nâng cao kiến thức, sẵn sàng bước vào kì thi vào lớp 10 sắp tới.
Đề thi thử vào lớp 10 lần 2 môn Toán trường THCS Hương Sơn, Hà Tĩnh năm 2015 - 2016
Đề thi tuyển sinh vào lớp 10 THPT môn Ngữ văn tỉnh Bắc Giang năm 2015 - 2016
SỞ GIÁO DỤC VÀ ĐÀO TẠO BẮC GIANG ĐỀ CHÍNH THỨC | ĐỀ TUYỂN SINH LỚP 10 TRUNG HỌC PHỔ THÔNG NĂM HỌC 2015 - 2016 MÔN THI: TOÁN Ngày thi: 19/7/2015 Thời gian làm bài 120 phút, không kể thời gian giao đề |
Câu I. (2,0 điểm)
1. Tính giá trị của biểu thức A = 2(5√16 - 4√25) + √64
2. Biết đồ thị của hàm số y = (1/3)ax2, (a ‡ 0) đi qua điểm M(3;-6), hãy xác định giá trị của a.
Câu II (3.0 điểm)
1. Giải hệ phương trình:
![]()
2. Rút gọn biểu thức:
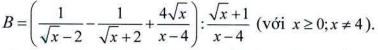
3. Cho phương trình x2 - (m2 + 3)x + 2m2 + 2 = 0 (x là ẩn, m là tham số) (1)
a. Giải phương trình (1) với m = -3
b. Tìm m để phương trình (1) có hai nghiệm phân biệt lớn hơn 1.
Câu III (1,5 điểm)
Nhà bạn Dũng được ông bà nội cho một mảnh đất hình chữ nhật. Khi bạn Nam đến nhà bạn Dũng chơi, Dũng đố Nam tìm ra kích thước của mảnh đất khi cho biết: mảnh đất có chiều dài gấp 4 lần chiều rộng và nếu giảm chiều rộng đi 2m, tăng chiều dài lên gấp đôi thì diện tích mảnh đất đó sẽ tăng thêm 20m2. Các em hãy giúp bạn Nam tìm ra chiều dài và chiều rộng của mảnh đất nhà bạn Dũng đó.
Câu IV (3 điểm)
Trên đường tròn (O) có đường kính AB = 2R, lấy một điểm C sao cho AC = R và lấy điểm D bất kỳ trên cung nhỏ BC (điểm D không trùng với B và C). Gọi E là giao điểm của AD và BC. Đường thẳng đi qua điểm E và vuông góc với đường thẳng AB tại điểm H cắt tia AC tại điểm F. Điểm M là trung điểm của đoạn EF.
1. Chứng minh tứ giác BHCF là tứ giác nội tiếp.
2. Chứng minh HA.HB = HE.HF.
3. Chứng minh CM là tiếp tuyến của đường tròn (O).
4. Xác định vị trí của điểm D để chu vi của tứ giác ABDC lớn nhất.
Câu V (0,5 điểm)
Cho ba số thực dương x, y, z thỏa mãn xy + xz + yz = 2016.
Chứng minh rằng:
![]()
Đáp án đề thi vào lớp 10 THPT môn Toán tỉnh Bắc Giang
Câu 1:
A = 2(5√16 - 4√25) + √64 = 2(5.4 - 4.5) + 8
= 2(20 - 20) + 8 = 8.
Đồ thị hàm số y = (1/3)ax2, (a 0) đi qua điểm M(3;-6) khi -6 = (1/3)a.32
↔ -6 = 3a
↔ a = -2
Vậy a = -2 là giá trị cần tìm
Câu 2.1:

Câu 2.2:

Câu 3:
a. Với m = -√3 ta được phương trình x2 - 6x + 8 = 0
Tính được Δ' = 1
KL được phương trình (1) có hai nghiệm x1 = 2; x2 = 4.
b. Khẳng định được phương trình (1) có hai nghiệm phân biệt x1 = 2; x2 = m2 + 1 khi m ≠ -1 và m ≠ 1.
Để phương trình (1) có hai nghiệm phân biệt đều lớn hơn 1 thì m2 + 1 > 1 m ≠ 0.
Kết luận: Với m ≠ -1, m ≠ 0 và m ≠ 1 thỏa mãn yêu cầu đầu bài.
(Còn tiếp)