Giá trị lượng giác của một cung
Chuyên đề Toán học lớp 10: Giá trị lượng giác của một cung được VnDoc sưu tầm và giới thiệu tới các bạn học sinh cùng quý thầy cô tham khảo. Nội dung tài liệu sẽ giúp các bạn học sinh học tốt môn Toán học lớp 10 hiệu quả hơn. Mời các bạn tham khảo.
Chuyên đề: Giá trị lượng giác của một cung
I. GIÁ TRỊ LƯỢNG GIÁC CỦA CUNG α
1. Định nghĩa
Trên đường tròn lượng giác cho cung ![]() có sđ
có sđ ![]() = α (còn viết
= α (còn viết ![]() = α)
= α)
Tung độ y = ![]() của điểm M gọi là sin của α và kí hiệu là sinα
của điểm M gọi là sin của α và kí hiệu là sinα
sin α = ![]()
Hoành độ x = ![]() của điểm M gọi là côsin của α và kí hiệu là cosα
của điểm M gọi là côsin của α và kí hiệu là cosα
cos α = ![]()
Nếu cos α ≠ 0, tỉ số ![]() gọi là tang của α và kí hiệu là tan α (người ta còn dùng kí hiệu tg α)
gọi là tang của α và kí hiệu là tan α (người ta còn dùng kí hiệu tg α)
Tan α = ![]()
Nếu sinα ≠ 0 tỉ số ![]() gọi là côtang của α và kí hiệu là cotα (người ta còn dùng kí hiệu cotg α)
gọi là côtang của α và kí hiệu là cotα (người ta còn dùng kí hiệu cotg α)
 Các giá trị sinα, cosα, tanα, cotα được gọi là các giá trị lượng giác của cung α. Ta cũng gọi trục tung là trục sin, còn trục hoành là trục côsin
Các giá trị sinα, cosα, tanα, cotα được gọi là các giá trị lượng giác của cung α. Ta cũng gọi trục tung là trục sin, còn trục hoành là trục côsin
2. Hệ quả
1) sinα và cosα xác định với mọi α ∈ R. Hơn nữa, ta có
sin(α + k2π) = sin α, ∀k ∈ Z;
cos(α + k2π) = cos α, ∀k ∈ Z
2) Vì –1 ≤ ![]() ≤ 1; –1 ≤
≤ 1; –1 ≤ ![]() ≤ 1 nên ta có
≤ 1 nên ta có
–1 ≤ sin α ≤ 1
–1 ≤ cos α ≤ 1
3) Với mọi m ∈ R mà –1 ≤ m ≤ 1 đều tồn tại α và β sao cho sin α = m và cos β = m.
4) tanα xác định với mọi α ≠ ![]() + kπ (k ∈ Z)
+ kπ (k ∈ Z)
5) cotα xác định với mọi α ≠ kπ (k ∈ Z)
6) Dấu của các giá trị lượng giác của góc α phụ thuộc vào vị trí điểm cuối của cung = α trên đường tròn lượng giác.
Bảng xác định dấu của các giá trị lượng giác
| Giá trị lượng giác |Góc phần tư | I | II | III | IV |
| cos α | + | - | - | + |
| sin α | + | + | - | - |
| tan α | + | - | + | - |
| cot α | + | - | + | - |
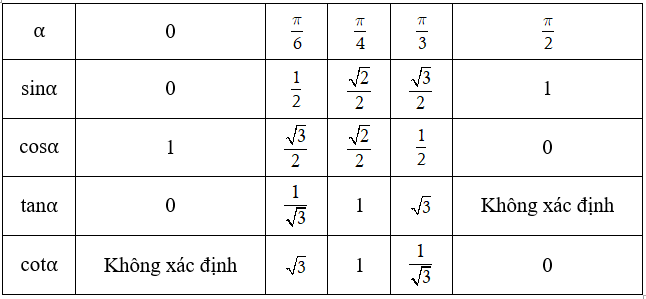
3. Giá trị lượng giác của các cung đặc biệt
II. Ý NGHĨA HÌNH HỌC CỦA TANG VÀ CÔTANG
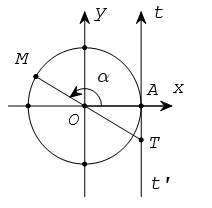
1. Ý nghĩa hình học của tan α
Từ A vẽ tiếp tuyến t’At với đường tròn lượng giác. Ta coi tiếp tuyến này là một trục số bằng cách chọn gốc tại A.
Gọi T là giao điểm của OM với trục t’At.
tanα được biểu diễn bởi độ dài đại số của vectơ ![]() trên trục t’At. Trục t’At được gọi là trục tang.
trên trục t’At. Trục t’At được gọi là trục tang.
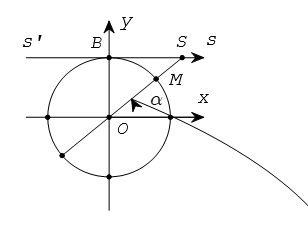
2. Ý nghĩa hình học của cot α
Từ B vẽ tiếp tuyến s’Bs với đường tròn lượng giác. Ta coi tiếp tuyến này là một trục số bằng cách chọn gốc tại B.
Gọi S là giao điểm của OM với trục s’Bs
cot α được biểu diển bởi độ dài đại số của vectơ ![]() trên trục s’Bs. Trục s’Bs được gọi là trục côtang.
trên trục s’Bs. Trục s’Bs được gọi là trục côtang.
III – QUAN HỆ GIỮA CÁC GIÁ TRỊ LƯỢNG GIÁC
1. Công thức lượng giác cơ bản
Đối với các giá trị lượng giác, ta có các hằng đẳng thức sau
sin2α + cos2α = 1
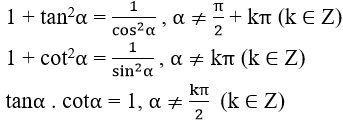
2. Giá trị lượng giác của các cung có liên quan đặc biệt
1) Cung đối nhau: α và –α
cos(-α) = cosα
sin(-α) = –sinα
tan(-α) = –tanα
cot(-α) = –cotα
2) Cung bù nhau: α và π-α
sin(π-α) = sinα
cos(π-α) = –cosα
tan(π-α) = –tanα
cot(π-α) = –cotα
3) Cung hơn kém π : α và (α + π)
sin(α + π) = –sinα
cos(α + π) = –cosα
tan(α + π) = tanα
cot(α + π) = cotα
4) Cung phụ nhau: α và (![]() – α)
– α)
sin(![]() – α) = cosα
– α) = cosα
cos(![]() – α) = sinα
– α) = sinα
tan(![]() – α) = cotα
– α) = cotα
cot(![]() – α) = tanα
– α) = tanα
Trên đây VnDoc đã giới thiệu tới các bạn lý thuyết môn Toán học 10: Giá trị lượng giác của một cung. Để có kết quả cao hơn trong học tập, VnDoc xin giới thiệu tới các bạn học sinh tài liệu Chuyên đề Toán học 10, Giải bài tập Toán lớp 10, Giải SBT Toán 10, Giải VBT Toán lớp 10 mà VnDoc tổng hợp và giới thiệu tới các bạn đọc