Giải Toán 9 bài 4 Liên hệ giữa phép chia và phép khai phương
Giải SGK Toán 9 bài 4: Liên hệ giữa phép chia và phép khai phương giúp các em trả lời các câu hỏi trong SGK Toán 9 tập 1 trang 18, 19, 20. Với hướng dẫn giải chi tiết giúp các em học sinh có thêm tài liệu tham khảo, so sánh đánh giá kết quả, từ đó học tốt môn Toán lớp 9. Dưới đây là chi tiết bài tập, các em tham khảo nhé.
Giải Toán 9 bài 4: Liên hệ giữa phép chia và phép khai phương
- A. Trả lời câu hỏi trang 16, 17, 18 SGK Toán 9 tập 1
- B. Giải bài tập trang 18, 19, 20 sgk Toán 9 tập 1
- Bài 28 trang 18 sgk Toán 9 tập 1
- Bài 29 trang 19 sgk Toán 9 tập 1
- Bài 30 trang 19 sgk Toán 9 tập 1
- Bài 31 trang 19 sgk Toán 9 tập 1
- Bài 32 trang 19 sgk Toán 9 tập 1
- Bài 33 trang 19 sgk Toán 9 tập 1
- Bài 34 trang 19 sgk Toán 9 tập 1
- Bài 35 trang 20 sgk Toán 9 tập 1
- Bài 36 trang 20 SGK Toán 9 tập 1
- Bài 37 trang 20 SGK Toán 9 tập 1
- C. Trắc nghiệm Toán 9 bài 4
A. Trả lời câu hỏi trang 16, 17, 18 SGK Toán 9 tập 1
Câu hỏi 1 trang 16 SGK Toán 9 tập 1
Tính và so sánh: ![]() và
và ![]()
Hướng dẫn giải:

Câu hỏi 2 trang 17 SGK Toán 9 tập 1
Tính:
| a. | b. |
Hướng dẫn giải:
a. 
b. 
Câu hỏi 3 trang 18 SGK Toán 9 tập 1
Tính:
a.  | b.  |
Hướng dẫn giải:
a. 
b. 
Câu hỏi 3 trang 18 SGK Toán 9 tập 1
Rút gọn:
a. ![]() b.
b.  với
với ![]()
Hướng dẫn giải:
a. 
Khi ![]()
Khi ![]()
B. Giải bài tập trang 18, 19, 20 sgk Toán 9 tập 1
Bài 28 trang 18 sgk Toán 9 tập 1
Tính
![]()
![]()
![]()

Hướng dẫn giải:
a) Ta có:

b) Ta có:
![]()

c) Ta có:

![]()
d) Ta có:

Bài 29 trang 19 sgk Toán 9 tập 1
Tính




Hướng dẫn giải:


![]()

![]()


Bài 30 trang 19 sgk Toán 9 tập 1
Rút gọn các biểu thức sau:
 với
với ![]()
 với
với ![]()
 với
với ![]()
 với
với ![]()
Hướng dẫn giải:
a) Ta có:


Vì ![]() nên
nên ![]()
Vì ![]() nên
nên ![]()

Vậy 
b) Ta có:


Vì ![]()
Vì ![]() nên
nên ![]()

![]()
Vậy 
c) Ta có:


Vì ![]()
Vì ![]()

![=\dfrac{[5.(-5)].(x.x).y}{y^2.y}=\dfrac{-25x^2}{y^2}](https://i.vdoc.vn/data/image/holder.png)
Vậy 
d) Ta có:



Bài 31 trang 19 sgk Toán 9 tập 1
Đề bài
a) So sánh ![]() và
và ![]()
b) Chứng minh rằng: với ![]() thì
thì ![]()
a) Ta có:
![]()
![]()
Vì ![]()
Vậy ![]()
b Theo bài 26, ta đã chứng minh được: Với a>0 và b>0 thì:
![]()
Theo giải thiết, ta có
+) ![]()
+) ![]()
Áp dụng bài 26 cho hai số a-b và b, ta được:
![]()
![]()
![]()
![]()
Bài 32 trang 19 sgk Toán 9 tập 1
Tính
![]()
![]()


a) Ta có:
![]()
![]()
![]()
![]()


![]()
b) Ta có:
![]()
![]()
![]()
![]()
![]()
c) Ta có:

![]()

Câu d: Ta có:

![]()
Bài 33 trang 19 sgk Toán 9 tập 1
Giải phương trình
a) ![]()
b) ![]()
c) ![]()
d) 
Hướng dẫn giải:
a)
![]()
![]()

![]()
![]()
![]()
![]()
Vậy ![]()
b)
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Vậy ![]()
c)
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Vậy ![]()
d)


![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Vậy ![]()
Bài 34 trang 19 sgk Toán 9 tập 1
Rút gọn các biểu thức sau:
a)  với
với ![]()
b)  với
với ![]()
c)  với
với ![]() và
và ![]()
d)  với
với ![]()
Hướng dẫn giải:
a) Ta có:



(Vì ![]() nên
nên ![]() và
và ![]() nên
nên ![]()
b) Ta có:

![]()

![]()
( Vì ![]() nên
nên ![]()
c) Ta có:



Vì ![]()
![]()
![]()
![]()
![]()
Vì ![]()
Do đó: 
Vậy 
d) Ta có:



Bài 35 trang 20 sgk Toán 9 tập 1
Tìm x, biết:
a) ![]()
b) ![]()
Hướng dẫn giải:
a) Ta có:
![]()
![]()
![]()
Vậy phương trình đã cho có hai nghiệm: ![]() và
và ![]()
b) Ta có:
![]()
![]()
![]()
![]()

Vậy phương trình có 2 nghiệm ![]() và
và ![]()
Bài 36 trang 20 SGK Toán 9 tập 1
Mỗi khẳng định sau đúng hay sai? Vì sao?
![]()
![]()
![]() và
và ![]()
![]()
Hướng dẫn giải:
a) Đúng.
Vì ![]()
b) Sai.
Vì số âm không có căn bậc hai.
c) Đúng. Vì:

Mà ![]()
![]()
![]()
Hay ![]() và
và ![]()
d) Đúng.
Xét bất phương trình đề cho:
![]()
Ta có:

Mà ![]()
![]()
![]()
![]()
Chia cả hai vế của bất đẳng thức ![]() cho số dương
cho số dương ![]() , ta được:
, ta được:

![]()
Vậy phép biến đổi tương đương trong câu d là đúng.
Bài 37 trang 20 SGK Toán 9 tập 1
Đố:
Trên lưới ô vuông, mỗi ô vuông cạnh
Đố: Trên lưới ô vuông, mỗi ô vuông cạnh 1cm1cm, cho bốn điểm M, N, P, QM, N, P, Q (h.3).
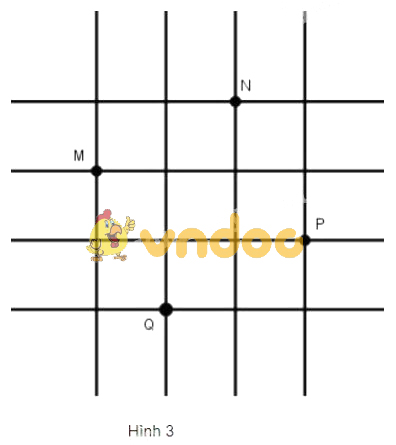
Hãy xác định số đo cạnh, đường chéo và diện tích của tứ giác MNPQMNPQ.
Hướng dẫn giải:
Nối các điểm ta có tứ giác MNPQ
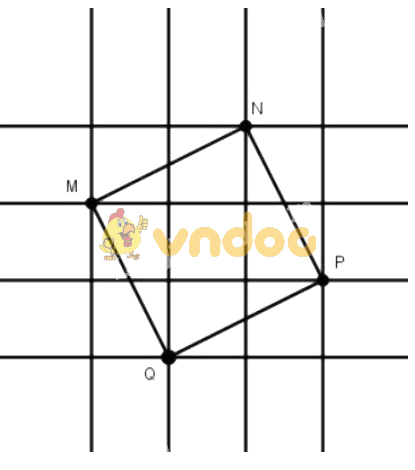
Tứ giác MNPQ có:
- Các cạnh bằng nhau và cùng bằng đường chéo của hình chữ nhật có chiều dài 2cm, chiều rộng 1cm. Do đó theo định lí Py-ta-go:
![]()
- Các đường chéo bằng nhau và cùng bằng đường chéo của hình chữ nhật có chiều dài 3cm, chiều rộng 1cm nên độ dài đường chéo là:
![]()
Từ các kết quả trên suy ra MNPQ là hình vuông. Vậy diện tích tứ giác MNPQ bằng ![]()
C. Trắc nghiệm Toán 9 bài 4
..........................
Ngoài tài liệu trên, mời các bạn tham khảo thêm Giải Toán 9, Tài liệu học tập lớp 9, và các đề học kì 1 lớp 9 và đề thi học kì 2 lớp 9 mới nhất được cập nhật.
![]() Bài tiếp theo: Giải Toán 9 bài 5: Bảng Căn bậc hai
Bài tiếp theo: Giải Toán 9 bài 5: Bảng Căn bậc hai