Giải SBT Toán 12 bài 4: Hàm số mũ. Hàm số logarit
Toán 12 - Hàm số mũ. Hàm số logarit
VnDoc mời bạn đọc tham khảo tài liệu Giải SBT Toán 12 bài 4: Hàm số mũ. Hàm số logarit, với nội dung được cập nhật chi tiết và chính xác nhất sẽ giúp các bạn giải Toán một cách hiệu quả hơn. Mời các bạn học sinh tham khảo.
Giải SBT Toán 12 bài tập trắc nghiệm chương 1: Ứng dụng đạo hàm để khảo sát và vẽ đồ thị của hàm số
Giải SBT Toán 12 bài 1: Lũy thừa
Giải SBT Toán 12 bài 4
Bài 2.18 trang 115 Sách bài tập (SBT) Giải tích 12
Hãy so sánh mỗi số sau với 1.
a) ![]()
b) ![]()
c) ![]()
d) ![]()
Hướng dẫn làm bài:
a) ![]()
b) ![]()
c) ![]()
d) ![]()
Bài 2.19 trang 115 Sách bài tập (SBT) Giải tích 12
Tìm tọa độ giao điểm của đồ thị của mỗi cặp hàm số sau:
a) ![]() và y = 8
và y = 8
b) ![]() và
và ![]()
c) ![]() và
và ![]()
d) ![]() và y = 9
và y = 9
Hướng dẫn làm bài:
a) (3; 8)
b) ![]()
c) ![]()
d) (-2; 9).
Bài 2.20 trang 116 Sách bài tập (SBT) Giải tích 12
Sử dụng tính chất đồng biến, nghịch biến của hàm số mũ, hãy so sánh mỗi cặp số sau:
a) (1,7)3 và 1
b) (0,3)2 và 1.
c) (3,2)1,5 và (3,2)1,6
d) (0,2)-3 và (0,2)-2
e) ![]() và
và ![]()
g) ![]() và 63,14
và 63,14
Hướng dẫn làm bài:
a) (1,7)3 > 1 ;
b) (0,3)2 < 1 ;
c) (3,2)1,5 < (3,2)1,6
d) (0,2)- 3 > (0,2)- 2
e) ![]()
g) ![]() .
.
Bài 2.21 trang 116 Sách bài tập (SBT) Giải tích 12
Từ đồ thị của hàm số y=3x, hãy vẽ đồ thị của các hàm số sau:
a) y = 3x– 2
b) y = 3x+ 2
c) y = |3x– 2|
d) y = 2 – 3x
Hướng dẫn làm bài:
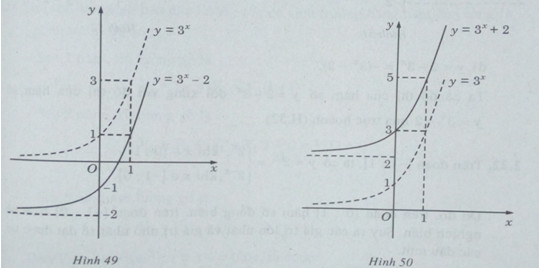
a) Đồ thị của hàm số y y=3x−2 nhận được từ đồ thị của hàm số y=3x bằng phép tịnh tiến song song với trục tung xuống dưới 2 đơn vị (H. 49)
b) Đồ thị của hàm số y=3x+2 nhận được từ đồ thị của hàm số y=3x bằng phép tịnh tiến song song với trục tung lên phía trên 2 đơn vị (H. 50)
c)
![]()
Do đó, đồ thị của hàm số y=|3x−2| gồm:
- Phần đồ thị của hàm số y=3x−2 ứng với 3x−2≥0 (nằm phía trên trục hoành).
- Phần đối xứng qua trục hoành của đồ thị hàm số y=3x−2 ứng với 3x−2<0.
Vậy đồ thị của hàm số y=|3x−2 có dạng như hình 51.

d) y=2−3x=−(3x−2)
Ta có đồ thị của hàm số y=2−3x đối xứng với đồ thị cua hàm số y=3x−2 qua trục hoành (H.52).
Bài 2.22 trang 116 Sách bài tập (SBT) Giải tích 12
Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số ![]() trên đoạn [-1; 1].
trên đoạn [-1; 1].
Hướng dẫn làm bài:
Trên đoạn [-1; 1], ta có:
![\begin{array}{l}
y = {\log _{\sqrt 5 }}x\\
y = {2^{|x|}} = \left\{ {\begin{array}{*{20}{c}}
{{2^x},khix \in {\rm{[}}0;1]}\\
{{2^{ - x}},khix \in {\rm{[}} - 1;0]}
\end{array}} \right.
\end{array}](https://i.vdoc.vn/data/image/holder.png)
Do đó, trên đoạn [0; 1] hàm số đồng biến, trên đoạn [-1; 0] hàm số nghịch biến. Suy ra các giá trị lớn nhất và giá trị nhỏ nhất sẽ đạt được tại các đầu mút.
Ta có: ![]()
Vậy ![]()
Bài 2.23 trang 116 Sách bài tập (SBT) Giải tích 12
Cho biết chu kỳ bán rã của một chất phóng xạ là 24 giờ (1 ngày đêm). Hỏi 250 gam chất đó sẽ còn lại bao nhiêu gam sau:
a) 1,5 ngày đêm?
B) 3,5 ngày đêm
Hướng dẫn làm bài:
Ta biết công thức tính khối lượng chất phóng xạ tại thời điểm t là:
![]()
Trong đó, m0 là khối lượng chất phóng xạ ban đầu. (tức là tại thời điểm t = 0).
T là chu kỳ bán rã.
Ta có: T = 24 giờ = 1 ngày đêm, m0 = 250 gam.
Do đó:
a) Khối lượng chất phóng xạ còn lại sau 1,5 ngày đêm là:
![]()
b) Khối lượng chất phóng xạ còn lại sau 3,5 ngày đêm là:
![]()
Bài 2.24 trang 116 Sách bài tập (SBT) Giải tích 12
Một khu rừng có trữ lượng gỗ 4.105 mét khối. Biết tốc độ sinh trưởng của các cây ở khu rừng đó là 4% mỗi năm. Hỏi sau 5 năm, khu rừng đó sẽ có bao nhiêu mét khối gỗ?
Hướng dẫn làm bài:
Gọi trữ lượng gỗ ban đầu là V0, tốc độ sinh trưởng hằng năm của rừng là i phần trăm. Ta có:
- Sau 1 năm, trữ lượng gỗ là:
V1 = V0 + iV0 = V0(1 + i)
- Sau 2 năm, trữ lượng gỗ là:
V2 = V1 + iV1 = V1(1 + i) = V0(1 + i)2
………………
- Sau 5 năm, trữ lượng gỗ là
V5 = V0(1 + i)5
Thay V0 = 4.105 (m3), i = 4% = 0,04, ta được
V5 = 4.105 (1 + 0,04)5 = 4,8666.105 (m3).
Bài 2.25 trang 116 Sách bài tập (SBT) Giải tích 12
Tìm tập xác định của các hàm số sau:
a) ![]()
b) ![]()
c) ![]()
d) ![]()
e) ![]()
g) ![]()
Hướng dẫn làm bài:
a) ![]()
b) ![]()
c) ![]()
d) ![]()
e) ![]()
g) ![]()
Bài 2.26 trang 116 Sách bài tập (SBT) Giải tích 12
Tình đạo hàm của các hàm số đã cho ở bài tập 2.25.
a) ![]()
b) ![]()
c) ![]()
d) ![]()
e) ![]()
g) ![]()
Hướng dẫn làm bài:
a) ![]()
b) 
c) 
d) ![]()
e) ![]()
g) 
Bài 2.27 trang 116 Sách bài tập (SBT) Giải tích 12
Từ đồ thị của hàm số ![]() , hãy vẽ đồ thị của các hàm số sau:
, hãy vẽ đồ thị của các hàm số sau:
a) ![]()
b) ![]()
c) ![]()
d) ![]()
Hướng dẫn làm bài:
a)
![]()
Do đó, đồ thị của hàm số ![]() gồm:
gồm:
- Phần đồ thị của hàm số ![]() ứng với
ứng với ![]()
- Phần đối xứng qua trục hoành của đồ thị hàm số ![]() ứng với 0 < x < 1.
ứng với 0 < x < 1.
Vậy đồ thị có dạng như Hình 53.
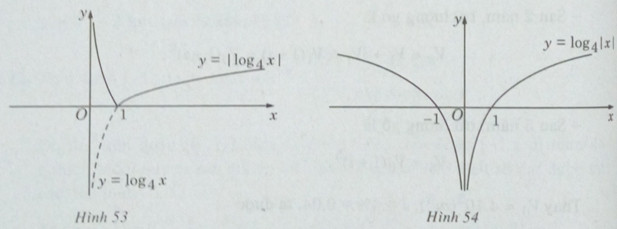
b) Hàm số ![]() có tập xác định D = R\{0} và là hàm số chẵn vì:
có tập xác định D = R\{0} và là hàm số chẵn vì:
![]()
Do đó, đồ thị của hàm số này có trục đối xứng là trục tung, trong đó phần đồ thị ứng với x > 0 là đồ thị của hàm số ![]()
Vậy ta có đồ thị như Hình 54.
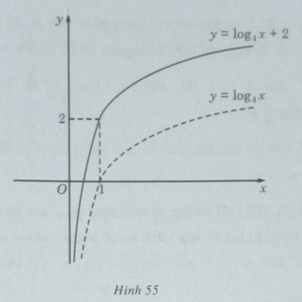
c) Đồ thị của hàm số nhận được từ đồ thị của hàm số bằng phép tịnh tiến song song với trục tung lên trên 2 đơn vị (H.55)
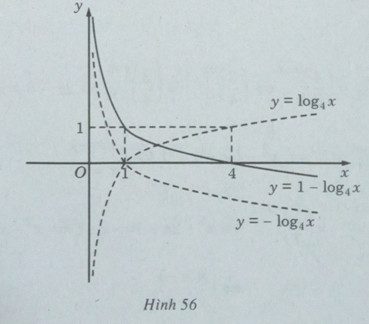
d) Để vẽ đồ thị của hàm số ![]() , ta thực hiện các bước sau:
, ta thực hiện các bước sau:
- Lấy đối xứng qua trục hoành đồ thị của hàm số ![]() để được đồ thị của hàm số
để được đồ thị của hàm số ![]() ;
;
- Tịnh tiến song song với trục tung đồ thị của hàm số ![]() lên phía trên 1 đơn vị.
lên phía trên 1 đơn vị.
Vậy ta có đồ thị của hàm số ![]() như trên Hình 56.
như trên Hình 56.
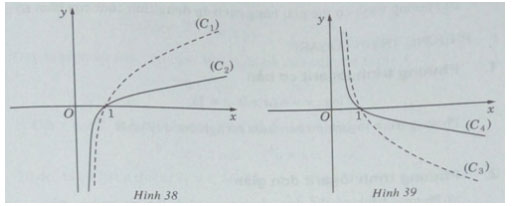
Bài 2.28 trang 116 Sách bài tập (SBT) Giải tích 12
Các hình 38 và 39 là đồ thị của bốn hàm số:
![]()
Hãy chỉ rõ đồ thị tương ứng với mỗi hàm số và giải thích.
Hướng dẫn làm bài:
Ta có (C1), (C2) đi lên từ trái sang phải nên là đồ thị của các hàm số đồng biến, tức là ứng với hàm số logarit có cơ số lớn hơn 1.
Mặt khác, khi x > 1 thì ![]() và khi 0 < x < 1 thì
và khi 0 < x < 1 thì ![]()
Do đó, (C1) là đồ thị của hàm số ![]() , (C2) là đồ thị của hàm số
, (C2) là đồ thị của hàm số ![]()
Ta có (C3), (C4) đi xuống từ trái sang phải nên là đồ thị của các hàm số nghịch biến, nghĩa là ứng với hàm số logarit có cơ số nhỏ hơn 1.
Mặt khác, khi x > 1 thì ![]() và khi 0 < x < 1 thì
và khi 0 < x < 1 thì ![]()
Do đó, (C3) là đồ thị của hàm số ![]() ; (C4) là đồ thị của hàm số
; (C4) là đồ thị của hàm số ![]()
Bài 2.29 trang 116 Sách bài tập (SBT) Giải tích 12
Hãy so sánh x với 1, biết rằng:
a) ![]()
b) ![]()
c) ![]()
d) ![]()
Hướng dẫn làm bài:
a) x < 1
b) x < 1
c) x > 1
d) x > 1.
-------------------------
Trên đây VnDoc.com đã giới thiệu tới bạn đọc tài liệu: Giải SBT Toán 12 bài 4: Hàm số mũ. Hàm số logarit. Để có kết quả cao hơn trong học tập, VnDoc xin giới thiệu tới các bạn học sinh tài liệu Giải bài tập Toán lớp 12, Giải bài tập Hóa học lớp 12, Giải bài tập Vật Lí 12 mà VnDoc tổng hợp và đăng tải.