Sử dụng sơ đồ Hoocne (Horner) để chia đa thức
Phương pháp Hoocne trong chia đa thức
Sử dụng lược đồ Horner để chia đa thức môn Toán lớp 8, 9 được VnDoc biên soạn và đăng tải. Đây là tài liệu nâng cao kiến thức về cách chia đa thức. Phân tích đa thức thành nhân tử là kiến thức cơ bản cho các bài học về nhân chia đơn thức, đa thức. Đặc biệt trong các biểu thức phân số có chứa biến hay chia đa thức trong chương trình toán lớp 8 và các lớp sau.
Có rất nhiều cách để phân tích đa thức thành nhân tử. Tuy nhiên, có những bài toán đa thức các bạn học sinh sẽ gặp khó khăn trong việc phân tích chúng thành nhân tử. Bởi vậy, VnDoc giới thiệu tài liệu này để giúp các bạn học sinh tiếp cận được với phương pháp chia đa thức, phân tích đa thức nhân tử một cách tiết kiệm thời gian và chính xác. Qua đó sẽ giúp cho các bạn học sinh ôn tập và hiểu rõ hơn về Đa thức và cách chia đa thức cũng như ôn luyện thi học sinh giỏi. .
1. Giới thiệu về lược đồ Hoocne
Phân tích đa thức thành nhân tử là kiến thức cơ bản cho các bài học về nhân chia đơn thức, đa thức. Đặc biệt trong các biểu thức phân số có chứa biến hay chia đa thức trong chương trình toán lớp 8 và các lớp sau.
Có rất nhiều cách để phân tích đa thức thành nhân tử. Tuy nhiên, có những bài toán đa thức các bạn học sinh sẽ gặp khó khăn trong việc phân tích chúng thành nhân tử.
Bởi vậy, VnDoc giới thiệu tài liệu này để giúp các bạn học sinh tiếp cận được với phương pháp chia đa thức, phân tích đa thức nhân tử một cách tiết kiệm thời gian và chính xác.
2. Cách sử dụng lược đồ Hoocne
Sơ đồ Horner (Hoocne/ Hoắc - le/ Hắc - le) dùng để tìm đa thức thương và dư trong phép chia đa thức f(x) cho đa thức x - α , khi đó ta thực hiện như sau:
Giả sử cho đa thức
![]()
Khi đó đa thức thương ![]() và đa thức dư được xác định theo lược đồ sau:
và đa thức dư được xác định theo lược đồ sau:

Ta được cách làm theo các bước như sau:
Bước 1: Sắp xếp các hệ số của đa thức f(x) theo ẩn giảm dần và đặt số α vào cột đầu tiên của hàng thứ 2. Nếu trong đa thức mà khuyết ẩn nào đó thì ta coi hệ số của nó bằng 0 và vẫn phải điền vào lược đồ.
Bước 2: Cột thứ 2 của hàng 2 ta hạ hệ số a0 ở hàng trên xuống. Đây chính là hệ số đầu tiên của g(x) tìm được, tức là b0.
Bước 3: Lấy số α nhân với hệ số vừa tìm được ở hàng 2 rồi cộng chéo với hệ số hàng 1 (Ví dụ nếu ta muốn tìm hệ số b1 ở hàng thứ hai, trước tiên ta sẽ lấy α nhân với hệ số b0 sau đó cộng với hệ số a1 ở hàng trên; tương tự như vậy nếu ta muốn tìm hệ số b2 ở hàng thứ hai, trước tiên ta sẽ lấy α nhân với hệ số b1 sau đó cộng với hệ số a2 ở hàng trên,….)
Quy tắc nhớ: NHÂN NGANG, CỘNG CHÉO.
Bước 4: Cứ tiếp tục như vậy cho tới hệ số cuối cùng và kết quả ta sẽ có
![]()
hay
![]()
* Chú ý:
+ Bậc của đa thức g(x) luôn nhỏ hơn bậc của đa thức f(x) 1 đơn vị vì đa thức chia x - α có bậc là 1.
+ Nếu r = 0 thì đa thức f(x) chia hết cho đa thức g(x) và x = α sẽ là một nghiệm của đa thức f(x). Trong trường hợp này chính là phân tích đa thức thành nhân tử. Để tìm được α, ta sẽ nhẩm một nghiệm nguyên của đa thức f(x), α chính là nghiệm mà ta vừa nhẩm được.
Ví dụ 1: Thực hiện phép chia đa thức f(x) = x4 - 2x3 - 3x2 + 7x - 2 cho đa thức x + 3.
Lời giải:
Lưu ý rằng: nếu chia cho đa thức x - 3 thì α = 3, còn nếu chia cho đa thức x + 3 thì α = -3.
Dựa vào hướng dẫn trên ta sẽ có sơ đồ Hooc ne như sau:
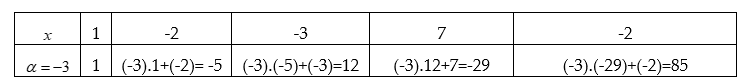
Đa thức g(x) tìm được ở đây chính là:
![]() và r = 85
và r = 85
Vậy khi chia đa thức f(x) = x4 - 2x3 - 3x2 + 7x - 2 cho đa thức x + 3 ta được:
f(x) = (x + 3)(x3 - 5x2 + 12x - 29) + 85
* Tuy nhiên không phải lúc nào bài toán cũng yêu cầu thực hiện phép chia đa thức bằng sơ đồ Hooc ne. Vậy thì trong một số trường hợp sau đây ta có thể sử dụng sơ đồ:
+ Chia đa thức cho đa thức một cách nhanh nhất.
+ Tìm nghiệm của phương trình bậc 3, phương trình bậc 4, phương trình bậc cao.
+ Phân tích đa thức thành nhân tử (với những đa thức có bậc lớn hơn 2).
Ví dụ 2: Tìm nghiệm của phương trình 2x3 - x2 - 5x - 2 = 0.
Lời giải:
Với phương trình này, khi ta bấm máy tính để tính nghiệm sẽ được 3 nghiệm của phương trình này là x = -1; x = 2; ![]()
Tuy nhiên, trong trình bày bài toán ta không thể viết “Theo máy tính ta được nghiệm của phương trình là….” mà ta sẽ đi phân tích đa thức f(x) = 2x3 - x2 - 5x -2 thành nhân tử.
Việc sử dụng máy tính sẽ cho ta biết được ít nhất 1 nghiệm nguyên của phương trình, từ đó ta có thể sử dụng sơ đồ Hooc ne để biến đổi.
Phương trình trên có một nghiệm nguyên x = -1 thì ta sẽ thực hiện phép chia đa thức f(x) cho đa thức x + 1.
Dựa vào hướng dẫn trên ta sẽ có sơ đồ Hooc ne như sau:
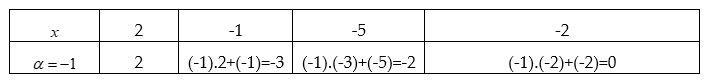
Vậy khi chia đa thức f(x) = x4 - 2x3 - 3x2 + 7x - 2 cho đa thức x + 1 ta được:
![]()
Việc thực hiện sơ đồ Hoocne ta chỉ nên thực hiện trong nháp. Khi trình bày ta sẽ trình bày như sau:
![]()

3. Bài tập vận dụng chia đa thức cho đa thức
3.1 Bài tập trắc nghiệm
Bài 1: Kết quả của phép chia ( 7x3 - 7x + 42 ):( x2 - 2x + 3 ) là ?
A. - 7x + 14
B. 7x + 14
C. 7x - 14
D. - 7x - 14
Chọn đáp án B.
Bài 2: Phép chia x3 + x2 - 4x + 7 cho x2 - 2x + 5 được đa thức dư là ?
A. 3x - 7.
B. - 3x - 8.
C. - 15x + 7.
D. - 3x - 7.
Chọn đáp án B.
Bài 3: Hệ số a thỏa mãn để 4x2 - 6x + a chia hết có x - 3 là ?
A. a = - 18.
B. a = 8.
C. a = 18.
D. a = - 8.
Chọn đáp án A.
Bài 4: Thực hiện phép chia: (4x4 + x + 2x3 - 3x2) : (x2 + 1) ta được số dư là :
A. – x + 7
B. 4x2 + 2x - 7
C. 4x2 – 2x + 7
D. x – 7
Chọn đáp án A
Bài 5: Thực hiện phép chia (3x3 + 2x + 1 ) : (x + 2) ta được đa thức dư là :
A. 10
B. -9
C. – 15
D. – 27
Chọn đáp án D
3.2 Bài tập tự luận
Bài 1: Thực hiện phép chia:
a) ![]()
b) ![]()
c) ![]()
d) ![]()
Bài 2: Làm phép chia bằng cách áp dụng hằng đẳng thức:
a) ![]()
b) ![]()
c) ![]()
d) ![]()
Bài 3: Sắp xếp các đa thức sau theo lũy thừa giảm của biến rồi làm phép chia:
a) ![]()
b) ![]()
c)![]()
Bài 4: Tìm m đề đa thức ![]() chia hết cho đa thức 3x-1
chia hết cho đa thức 3x-1
Bài 5 Tìm số dư trong phép chia đa thức ![]() cho đa thức
cho đa thức![]()
Bài 6: Phân tích các đa thức sau thành nhân tử:
a, ![]()
b, ![]()
c, ![]()
d, ![]()
Bài 7: Thực hiện phép chia đa thức:
a, ![]() cho
cho ![]()
b, ![]() cho
cho ![]()
c, ![]() cho
cho ![]()
d, ![]() cho
cho ![]()
Bài 8: Giải các phương trình sau:
a, ![]()
b, ![]()
c, ![]()
d, ![]()
------------
Trên đây, VnDoc đã chia sẻ tài liệu Sử dụng lược đồ Hoocne để chia đa thức. Hy vọng thông qua tài liệu này, các em học sinh sẽ nâng cao kỹ năng giải Toán, đặc biệt là chuyên đề chia đa thức cho đa thức trong Toán 8 và Toán 9.
- Chuyên đề xác định đa thức
- 200 đề thi học sinh giỏi lớp 8 môn Toán
- Chuyên đề số chính phương trong các đề thi học sinh giỏi
- Giải bài tập Toán lớp 9 trọn bộ
- Công thức nghiệm của phương trình bậc hai
- Cách tính delta và delta phẩy phương trình bậc 2
Ngoài chuyên đề sử dụng sơ đồ Hooc ne (Horner) để chia đa thức này, mời các bạn học sinh tham khảo thêm các tài liệu như tài liệu học tập lớp 8, tài liệu học tập lớp 9, đề thi học kì 1 lớp 8, đề thi học kì 2 lớp 8, đề thi học kì 2 lớp 9, đề thi học kì 2 lớp 9,... mà chúng tôi đã sưu tầm và chọn lọc. Với chuyên đề này sẽ giúp các bạn rèn luyện thêm kỹ năng giải đề và làm bài tốt hơn. Chúc các bạn học tập tốt!
Toán 8 từ năm học 2023 - 2024 trở đi sẽ được giảng dạy theo 3 bộ sách: Chân trời sáng tạo; Kết nối tri thức với cuộc sống và Cánh diều. Việc lựa chọn giảng dạy bộ sách nào sẽ tùy thuộc vào các trường. Để giúp các thầy cô và các em học sinh làm quen với từng bộ sách mới, VnDoc sẽ cung cấp lời giải bài tập sách giáo khoa, sách bài tập, trắc nghiệm toán từng bài và các tài liệu giảng dạy, học tập khác. Mời các bạn tham khảo qua đường link bên dưới: