Tìm hệ thức liên hệ giữa x1 x2 không phụ thuộc vào m
Chuyên đề luyện thi vào 10: Tìm hệ thức giữa hai nghệm x1 x2 không phụ thuộc vào tham số m
Tìm hệ thức liên hệ giữa hai nghiệm x1 x2 không phụ thuộc vào tham số m là một dạng toán thường gặp trong đề thi tuyển sinh vào lớp 10 môn Toán được VnDoc biên soạn và giới thiệu tới các bạn học sinh cùng quý thầy cô tham khảo. Nội dung tài liệu sẽ giúp các bạn học sinh học tốt môn Toán lớp 9, đồng thời chuẩn bị tốt cho kì thi vào lớp 10 môn Toán. Mời các bạn tham khảo chi tiết và tải về bài viết dưới đây nhé.
Tham khảo thêm: Đáp án đề thi vào lớp 10 năm 2023 - Tất cả các tỉnh
I. Kiến thức cần nhớ khi làm dạng bài Tìm hệ thức liên hệ giữa hai nghiệm x1, x2 không phụ thuộc vào m
1. Hệ thức vi ét
+ Nếu x1, x2 là hai nghiệm của phương trình ax2 + bc + c = 0 (a ≠ 0) thì

2. Ứng dụng vào bài toán
Để làm được bài toán này, ta lần lượt theo các bước sau:
+ Bước 1: Đặt điều kiện cho tham số để phương trình đã cho có hai nghiệm x1; x2
+ Bước 2: Áp dụng hệ thức Vi ét ![]() và
và ![]() rồi rút m từ các hệ thức đó
rồi rút m từ các hệ thức đó
+ Bước 3: Đồng nhất các vế ta sẽ tìm được hệ thức liên hệ giữa hai nghiệm
II. Bài tập ví dụ về bài toán Tìm hệ thức liên hệ giữa hai nghiệm x1, x2 không phụ thuộc vào m
Câu 1: Cho phương trình x2 + 2(m + 1)x + 2m = 0 (m là tham số). Tìm một hệ thức liên hệ giữa hai nghiệm của phương trình đã cho mà không phụ thuộc vào m.
Hướng dẫn
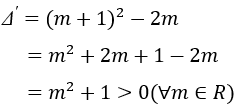
Vì ∆ꞌ > 0 với mọi m nên phương trình luôn có hai nghiệm x1, x2
Theo hệ thức Vi-et ta có :
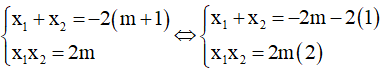
Lấy (1) + (2): (x1 + x2) + x1x2 = -2 không phụ thuộc vào m
Câu 2: Cho phương trình 2x2 + (2m – 1)x + m – 1 = 0 (m là tham số). Tìm một hệ thức liên hệ giữa hai nghiệm của phương trình đã cho mà không phụ thuộc vào m.
Hướng dẫn
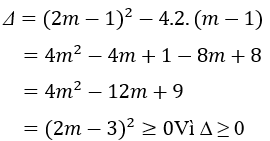
Vì ∆ ≥ 0 với mọi m nên phương trình luôn có hai nghiệm x1, x2
Theo hệ thức Vi-et ta có :
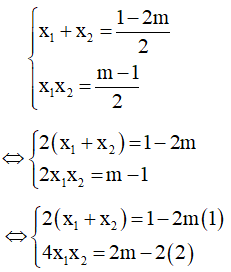
Lấy (1) + (2): 2(x1 + x2) +4x1x2 = -1 không phụ thuộc vào m
Câu 3. Cho phương trình x2 - 2(m - 1)x + m - 3 = 0
a, Tìm m để phương trình có hai nghiệm phân biệt x1; x2
b, Tìm hệ thức liên hệ giữa x1; x2 không phụ thuộc vào m
Hướng dẫn:
+ Điều kiện để phương trình trình bậc hai có hai nghiệm phân biệt x1; x2 là: ∆' > 0
Lời giải:
a, x2 - 2(m - 1)x + m - 3 = 0
∆' = b'2 - ac = (m - 1)2 - (m - 3) = m2 - 3m + 4  với mọi m
với mọi m
Vậy với mọi m thì phương trình có hai nghiệm phân biệt x1; x2
b, Với mọi m phương trình có hai nghiệm phân biệt x1; x2 thỏa mãn hệ thức Vi-ét:

Xét (1) ta có: ![]() (3)
(3)
Xét (2) ta có: m = x1x2 + 3 (4)
Đồng nhất các vế của (3) và (4) ta được hệ thức giữa hai nghiệm x1; x2 không phụ thuộc vào m:
![]() = x1x2 + 3 ⇔ x1 + x2 + 1 = 2x1x2 + 6 ⇔ x1 + x2 - 2x1x2 - 5 = 0
= x1x2 + 3 ⇔ x1 + x2 + 1 = 2x1x2 + 6 ⇔ x1 + x2 - 2x1x2 - 5 = 0
Câu 4: Tìm hệ thức liên hệ giữa hai nghiệm của phương trình:
![]() không phụ thuộc vào m
không phụ thuộc vào m
Hướng dẫn giải
Với ![]() thì:
thì: ![]()
Với ![]() thì
thì 
Để phương trình có nghiệm thì:
![]()
Áp dụng hệ thức Vi – ét ta có:

Cộng (1) với (2) ta được

III. Bài tập tự luyện về bài toán Tìm hệ thức liên hệ giữa hai nghiệm x1, x2 không phụ thuộc vào m
Bài 1: Cho phương trình (m - 1)x2 - 2mx + m + 1 = 0, với m là tham số:
a, Chứng minh phương trình có 2 nghiệm phân biệt với m khác 1
b, Tìm hệ thức liên hệ giữa hai nghiệm phân biệt của phương trình không phụ thuộc vào m
Bài 2: Cho phương trình x2 - 2(m - 1)x - m - 3 = 0 (m là tham số). Tìm hệ thức liên hệ giữa các nghiệm phân biệt x1; x2 không phụ thuộc giá trị của m
Bài 3: Cho phương trình (m - 1)2 - 2(m - 4)x + m - 5 = 0 (m là tham số)
a, Tìm m để phương trình có hai nghiệm phân biệt x1; x2
b, Tìm hệ thức liên hệ giữa hai nghiệm x1; x2 không phụ thuộc vào tham số m
Bài 4: Tìm hệ thức liên hệ giữa hai nghiệm phân biệt của phương trình x2 - (m + 3)x + 2m - 5 = 0 mà hệ thức này không phụ thuộc vào m
Bài 5: Cho phương trình bậc hai ẩn x: x2 - 2(m + 1)x + m - 4 = 0 (m là tham số)
a, Chứng minh phương trình luôn có hai nghiệm phân biệt x1; x2 với mọi giá trị của m
b, Tìm hệ thức liên hệ giữa hai nghiệm phân biệt của phương trình mà hệ thức này không phụ thuộc vào m
Bài 6: Cho phương trình bậc hai: x2 - 2(m + 4)x + m2 - 8 = 0 (1) (với m là tham số)
a, Tìm m để phương trình (1) có hai nghiệm phân biệt x1; x2
b, Tìm hệ thức liên hệ giữa hai nghiệm phân biệt của phương trình (1) mà hệ thức này không phụ thuộc vào m
-----------------
Để xem thêm các thông tin khác về kỳ thi tuyển sinh vào lớp 10 năm 2023, mời các bạn vào chuyên mục Thi vào lớp 10 trên VnDoc nhé. Chuyên mục tổng hợp các đề luyện thi vào lớp 10 THPT, cũng như các đề thi tuyển sinh vào lớp 10 trên cả nước, giúp các em rèn luyện thêm kỹ năng giải đề và làm bài tốt hơn. Bên cạnh đó là các thông tin về điểm chuẩn, điểm thi.... giúp các em dễ dàng theo dõi, cập nhật các thông tin quan trọng về tuyển sinh vào lớp 10 năm 2023.
Để tiện trao đổi, chia sẻ kinh nghiệm về giảng dạy và học tập các môn học lớp 9, VnDoc mời các thầy cô giáo, các bậc phụ huynh và các bạn học sinh truy cập nhóm riêng dành cho lớp 9 sau: Nhóm Luyện thi lớp 9 lên 10 . Rất mong nhận được sự ủng hộ của các thầy cô và các bạn.







