Tính chất đường trung trực của một đoạn thẳng
Chuyên đề Toán học lớp 7: Tính chất đường trung trực của một đoạn thẳng được VnDoc sưu tầm và giới thiệu tới các bạn học sinh cùng quý thầy cô tham khảo. Nội dung tài liệu sẽ giúp các bạn học sinh học tốt môn Toán học lớp 7 hiệu quả hơn. Mời các bạn tham khảo.
Chuyên đề: Tính chất đường trung trực của một đoạn thẳng
A. Lý thuyết
1. Định lý về tính chất các điểm thuộc đường trung trực
Điểm nằm trên đường trung trực của một đoạn thẳng thì cách đều hai mút của đoạn thẳng đó.
2. Định lý đảo
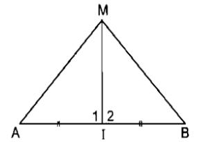
Điểm cách đều hai mút của một đoạn thẳng thì nằm trên đường trung trực của đoạn thẳng đó.
MA = MB ⇒ M thuộc đường trung trực của AB
Nhận xét: Từ hai định lý thuận và đảo, ta có: Tập hợp các điểm cách đều hai mút của một đoạn thẳng là đường trung trực của đoạn thẳng đó.
B. Trắc nghiệm & Tự luận
I. Câu hỏi trắc nghiệm
Bài 1: Gọi O là giao điểm của ba đường trung trực trong ΔABC. Khi đó O là:
A. Điểm cách đều ba cạnh của ΔABC
B. Điểm cách đều ba đỉnh của ΔABC
C. Tâm đường tròn ngoại tiếp ΔABC
D. Đáp án B và C đúng
Ba đường trung trực của một tam giác cùng đi qua một điểm. Điểm này cách đều ba đỉnh của tam giác và là tâm của đường tròn ngoại tiếp tam giác đó
Chọn đáp án D
Bài 2: Nếu một tam giác có một đường trung tuyến đồng thời là đường trung trực thì tam giác đó là tam giác gì?
A. Tam giác vuông
B. Tam giác cân
C. Tam giác đều
D. Tam giác vuông cân
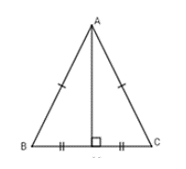
Giả sử ΔABC có AM là trung tuyến đồng thời là đường trung trưc. Ta sẽ chứng minh ΔABC là tam giác cân. Thật vậy, vì AM là trung tuyến của ΔABC (gt) ⇒ BM = MC (tính chất trung tuyến)
Vì AM là trung trực của BC ⇒ AM ⊥ BC
Xét hai tam giác vuông ΔABM và ΔACM có:
BM = CM (cmt)
AM chung
⇒ ΔABM = ΔACM (2 cạnh góc vuông)
⇒ AB = AC (2 cạnh tương ứng) ⇒ ΔABC cân tại A
Chọn đáp án D
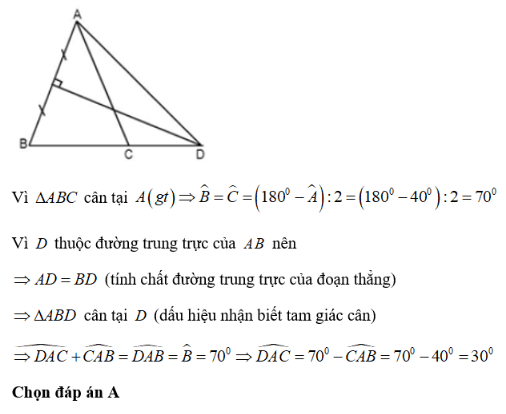
Bài 3: Cho ΔABC cân tại A , có ∠A = 40°, đường trung trực của AB cắt BC tại D . Tính ∠CAD
A. 30° B. 45° C. 60° D. 40°
Bài 4: Cho ΔABC cân tại A. Đường trung trực của AC cắt AB ở D. Biết CD là tia phân giác của ∠ACB. Tính các góc của ΔABC
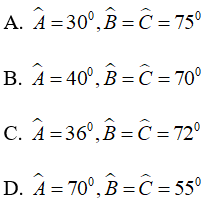
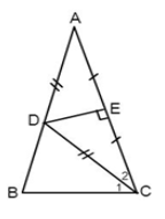
Vì đường trung trực của AC cắt AB ở D nên suy ra DA = DC (Tính chất đường trung trực của đoạn thẳng)
⇒ ΔDAC là tam giác cân tại D (dấu hiệu nhận biết tam giác cân)

Bài 5: Cho ΔABC vuông tại A, có ∠C = 30°, đường trung trực của BC cắt AC tại M. Em hãy chọn câu đúng:
A. BM là đường trung tuyến của ΔABC
B. BM = AB
C. BM là phân giác của ∠ABC
D. BM là đường trung trực của ΔABC
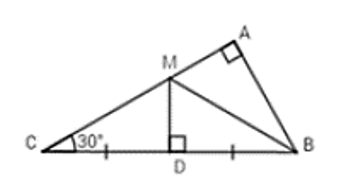
Vì M thuộc đường trung trực của BC ⇒ BM = MC (tính chất điểm thuộc đường trung trực của đoạn thẳng)
ΔBMC cân tại M (dấu hiệu nhận biết tam giác cân)

II. Bài tập tự luận
Bài 1: Cho đoạn thẳng AB thuộc nửa mặt phẳng bờ d. Xác định điểm M thuộc d sao cho M cách đều hai điểm A, B.
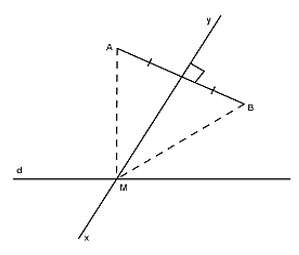
Vẽ trung trực xy của đoạn thẳng AB
Giả sử xy cắt d tại điểm M, ta có: MA = MB
+ Nếu AB ⊥ d thì xy // d, ta không xác định được điểm M
+ Ngoài trường hợp AB ⊥ d , ta luôn xác định được điểm M và M là duy nhất.
Bài 2: Cho tam giác ABC có AC > AB, phân giác AD. Trên AC lấy điểm E sao cho AE = AB. Chứng minh rằng AD vuông góc với BE.
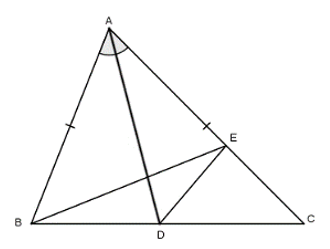
Nối BE và ED
Xét ΔADB và ΔADE có:
AD cạnh chung
∠BAD = ∠EAD (AD là tia phân giác góc BAC)
AB = AE (gt)
Do đó: ∠ADB = ∠ADE (c-g-c)
Suy ra DB = DE
Lại có AB = AE (gt)
Do đó AD là đường trung trực của BE
Hay AD vuông góc với BE
Trên đây VnDoc đã giới thiệu tới các bạn lý thuyết môn Toán học 7: Tính chất đường trung trực của một đoạn thẳng. Để có kết quả cao hơn trong học tập, VnDoc xin giới thiệu tới các bạn học sinh tài liệu Chuyên đề Toán học 7, Giải bài tập Toán lớp 7, Giải VBT Toán lớp 7 mà VnDoc tổng hợp và giới thiệu tới các bạn đọc