VnDoc.com

Tổng hợp kiến thức Hình học lớp 9

Tài liệu môn Toán lớp 9

110 78.171

1) Hệ thức về cạnh và đường cao trong tam giác vuông:

*AB

2

= BH. BC ; AC

2

= HC. BC

* AH

2

= BH. HC

* AB. AC = AH. BC

*

*Với 2 góc nhọn

;

* Nếu

*Tỷ số lượng giác của một số góc đặc biệt

Tỷ số

lượng giác

30

0

45

0

60

0

1

2

3

2

Cos

3

2

1

2

Tg

3

1

3

Cotg

3

1

3

3)Giải tam giác vuông :

B

A

C

H

A



Sin

B

a

c

b

A

C

a, b, c là độ dài 3 cạnh của tam giác ABC vuông tại A

* b = a.sinB = a.CosC ; c = a. sinC = a. cosB

* b = c.tgB = c.cotgC ; c = b.tgC = b.cotgB

huyền

đối

kề

huyền

đối

kề

đối

*ΔABC vuông tại A  BC =

AB = ; AC =

TỔNG HỢP KIẾN THỨC HÌNH HỌC LỚP 9

CHƯƠNG I: HỆ THỨC LƯỢNG TRONG TAM GIÁC

AH AB AC

1 1 1

2 2 2



* ΔABC vuông tại A  AB

2

+ AC

2

= BC

2

( Định lý Pythagore thuận, đảo)

2)Tỷ số lượng giác của một góc nhọn :

B





(= )

BC

AB





=

BC

AC

* Sin





=

AB

AC





= ; cot

* tan

AC

AB

* Cos

C



nếu ta có Sin

α



S

i

n

β (hoặc cos



= Cosβ ; tan



= tanβ ; cot



= cotβ

) thì

=





α +

β

=

9

0

thì ta có :

S

in



=

C

o

sβ

;

C

o

sα

=

S

in

β

; tan

α

=

c

o

t

β

; co

t

α

= tan

β

2

BC 3

 ΔABC vuông tại A có

B

= 60

0

 AC =

2

BC

 ΔABC vuông tại A có

C

= 30

0

 AB =

22

BC AB

22

BC AC

22

AB AC

1)Định nghĩa và sự xác định đường tròn:

a) Định nghĩa : Tập hợp các điểm cách điểm O cố định một khoảng không đổi bằng R là đường

tròn tâm O, bán kính R . Kí hiệu : đường tròn ( O; R ) hay đường tròn ( O ) .

b) Vị trí của một điểm đối với đường tròn :

* Điểm M nằm trên đường tròn ( O ; R )  OM = R .

* Điểm M nằm ngoài đường tròn ( O ; R )  OM > R .

* Điểm M nằm trong đường tròn ( O ; R )  OM < R .

* Định lý : Đường kính là dây cung lớn nhất của đường tròn .

Định lí :

* Đường tròn đi qua ba đỉnh A, B, C của tam giác ABC gọi là đường tròn ngoại tiếp tam giác ABC

( Tam giác ABC gọi là tam giác nội tiếp đường tròn )

* Tâm của đường tròn ngoại tiếp t/g là giao điểm các đường trung trực của các cạnh tam giác .

2) Tính chất đối xứng của đường tròn :

* Định lí : Trong một đường tròn :

*Đường thẳng và đường tròn không giao nhau :

- Số điểm chung : 0 ; - Hệ thức : d > R

*Định lí : Đường kính vuông góc với một dây thì đi qua trung điểm

của dây đó .

(Đường tròn ( O ) có OM ⊥ AB tại I  I là trung điểm của AB ).

*Định lí đảo : đường kính đi qua trung điểm của một dây (dây không

là đường kính ) thì vuông góc với dây đó . (Đường tròn ( O ) có OM

cắt AB tại I và I là trung điểm của dây AB  OM ⊥ AB tại I )

(Đường tròn ( O )có AB = CD, OI ⊥AB tạiI, OK ⊥CD tại K  OI = OK )

O

d

O

H

d

c) So sánh độ dài dây và đường kính :

d) Sự xác định của đường tròn:

A

B

M

I

O

N

b) Liên hệ giữa dây và khoảng cách đến tâm :

a) Liên hệ giữa đường kính và dây cung:

+ Hai dây bằng nhau thì cách đều tâm

+ Hai dây cách đều tâm thì bằng nhau

(Đường Tròn (O) có OI ⊥AB tại I, OK⊥CD tại K, OI = OK  AB = CD)

A

B

C

D

O

I

K

3)Vị trí tương đối của đường thẳng và đường tròn :

Ghi chú : d = OH là khoảng cách từ tâm đ. tròn ( O, R ) đến đ .thẳng a

*Đường thẳng và đường tròn cắt nhau :

a

- Số điểm chung : 2 ;- Hệ thức : d < R

+Trường hợp này đường thẳng a gọi là cát tuyến của

đường tròn ( O, R )

a

CHƯƠNG II: ĐƯỜNG TRÒN

* Định lí 1:( t/c của tiếp tuyến ) Nếu một đ.thẳng là tiếp tuyến của đ. tròn thì nó vuông góc với

b.kính đi qua t. điểm (Nếu a là tiếp tuyến của đ. tròn tâm O và H là tiếp điểm thì a ⊥OH hay a ⊥d )

* Định lí 2 ( dấu hiệu nhận biết tiếp tuyến ) Nếu một đường thẳng đi qua một điểm của đưòng tròn

và vuông góc với bán kính đi qua điểm đó thì đường thẳng ấy là tiếp tuyến của đường tròn .

( Đường tròn ( O , R ) có OH = R và OH ⊥ a thì a là tiếp tuyến của đường tròn ( O ) ).

* Định lí 3: ( tính chất hai tiếp tuyến cắt nhau ) Nếu MA và MB là hai tiếp tuyến của đường tròn (O)

+ Tâm của đường tròn nội tiếp tam giác là giao

điểm các đường phân giác trong của tam giác .

Ghi chú : d là khoảng cách hai tâm hai đường tròn ( O; R) và

( I ; r ), d = OI, giả sử R > r > 0 .

* Hai đường tròn không giao nhau :

- Số điểm chung : 0 ;-Hệ thức giữa d , R , r :

O

Ở ngoài nhau : d > R + r Đựng nhau : d < R – r Đặc biệt : đồng tâm ( d = 0 )

* Hai đường tròn cắt nhau : - Số điểm chung : 2

- Hệ thức giữa d, R, r là: R – r < d < R + r

+ Tính chất đường nối tâm : Nếu hai đường tròn cắt nhau thì đường

nối tâm vuông góc với dây chung và đi qua trung điểm của dây chung

( Nếu đường tròn (O) và đường tròn (I) cắt nhau tại hai điểm A và B thì

O

a

d

( A và B là hai tiếp điểm ) thì :

+ MA = MB .

+ OM là phân giác của góc AOB

+ MO là phân giác của góc AMB

A

B

C

O

* Đường tròn tiếp xúc với ba cạnh của tam giác ABC gọi là đường

tròn nội tiếp tam giác ABC ( Tam giác ABC gọi là tam giác ngoại

tiếp đường tròn )

B

A

I

O

I

O

r

R

F

E

I

O

I

* Đường thẳng và đường tròn tiếp xúc :

- Số điểm chung : 1 ; - Hệ thức : d = R

+ Trường hợp này đường thẳng a gọi là tiếp tuyến của

đường tròn ( O ; R )

và H gọi là tiếp điểm

H

+ OM ⊥ AB tại I ; I là trung điểm của AB ( OM là trung trực của AB )

O

A

B

M

5) Vị trí tương đối của hai đường tròn :

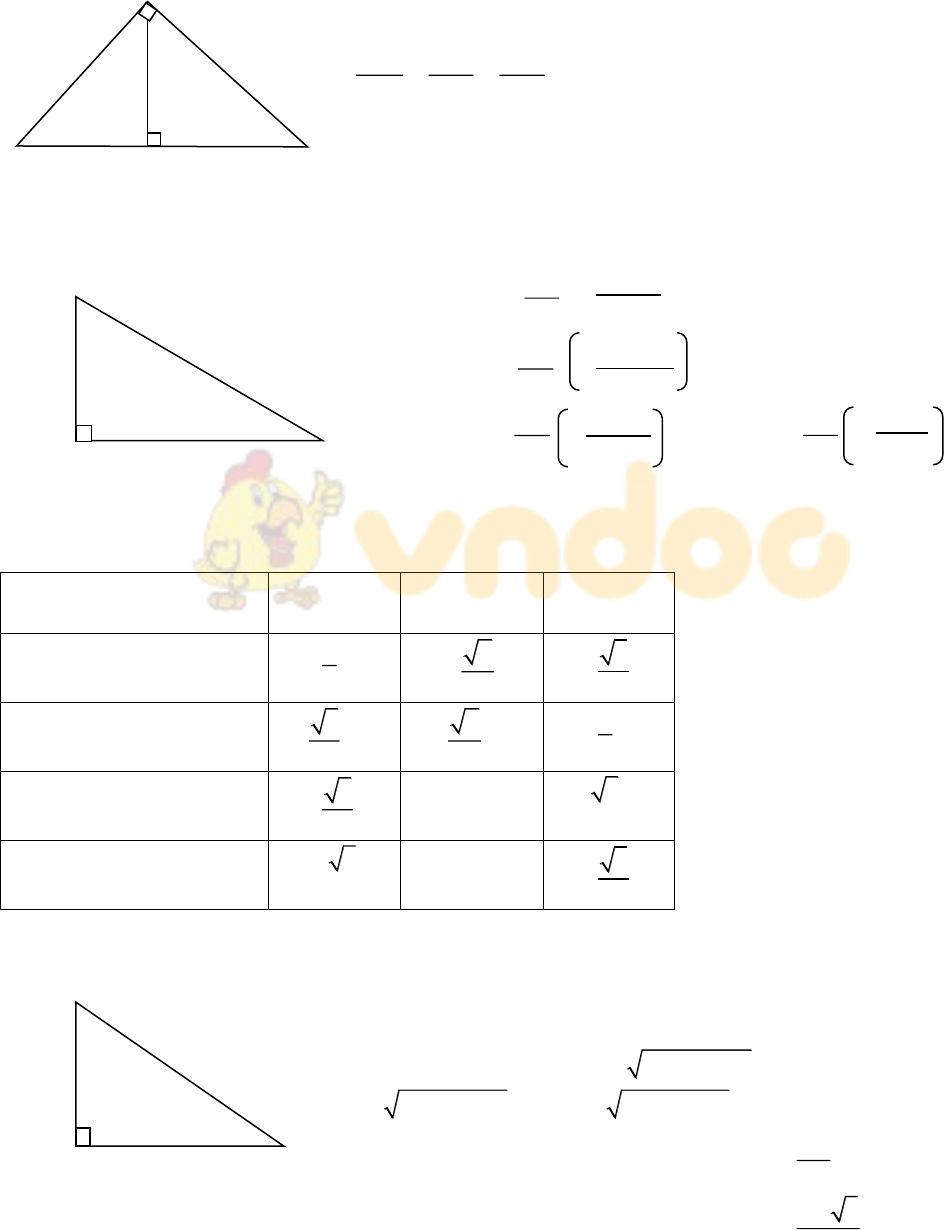
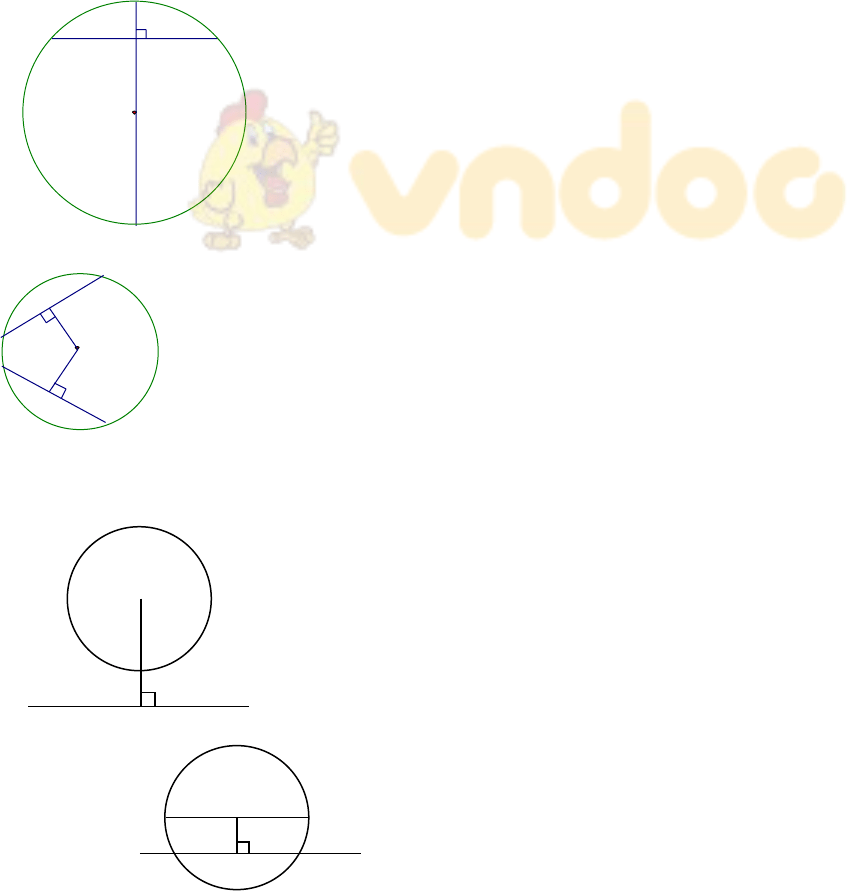
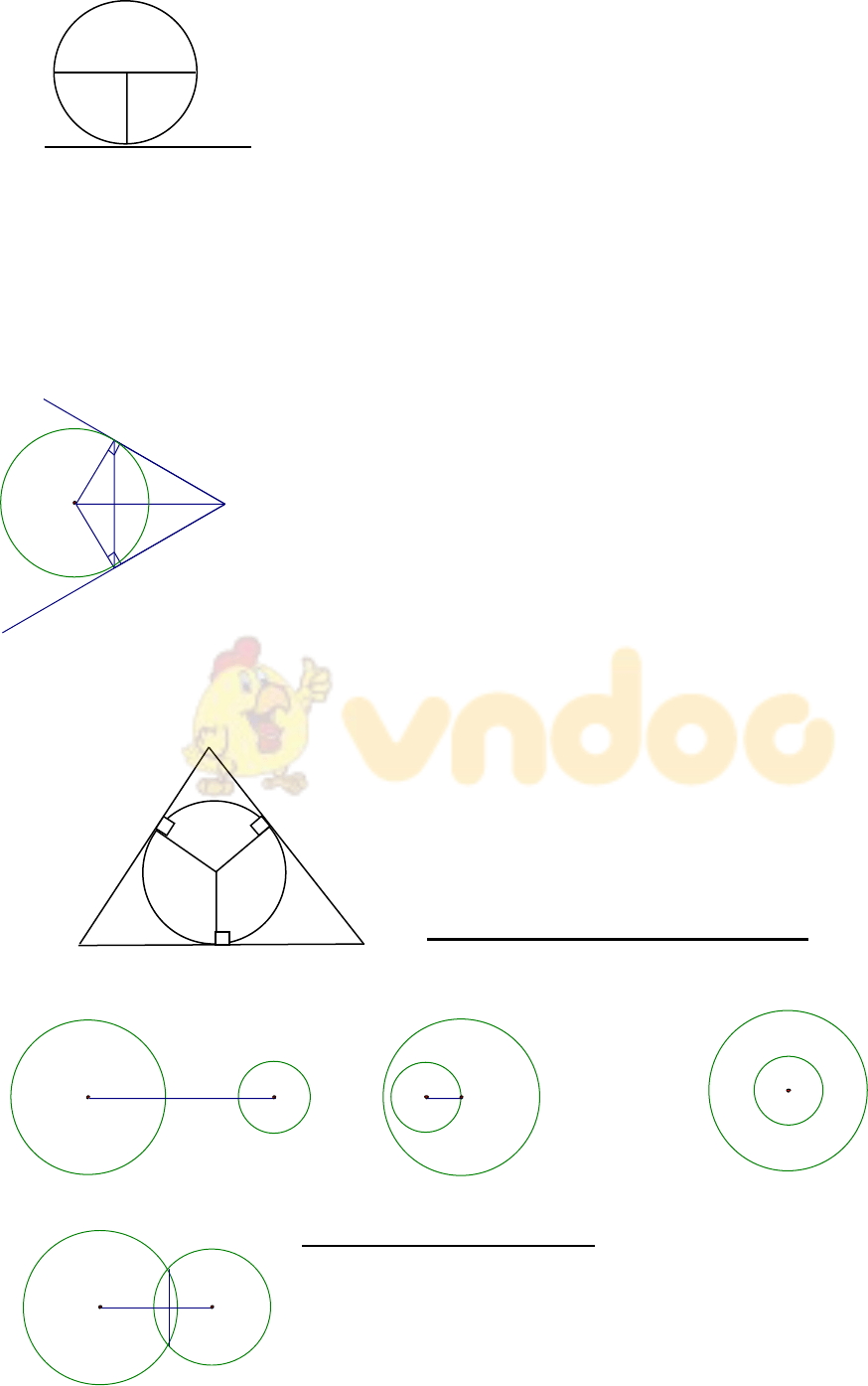
Hệ thống các kiến thức Hình học lớp 9

Tài liệu tổng hợp kiến thức Hình học lớp 9 tổng hợp và đăng tải. Tài liệu là tổng hợp kiến thức môn Toán lớp 9 gồm lý thuyết và các kiến thức cần nhớ để áp dụng giải toán. Trên đây là nội dung chi tiết các em tham khảo nhé

Ngoài ra, VnDoc.com đã thành lập group chia sẻ tài liệu học tập THCS miễn phí trên Facebook: Tài liệu học tập lớp 9. Mời các bạn học sinh tham gia nhóm, để có thể nhận được những tài liệu mới nhất.

Đây là tài liệu hệ thống các kiến thức về Hình học lớp 9 được tóm tắt một cách ngắn gọn nhất. Tài liệu được chia thành các chương theo chuẩn chương trình Sách giáo khoa của Học kì 1 và Học kì 2, ở mỗi chương sẽ tổng hợp lại các công thức quan trọng, được vận dụng trong các bài toán. Qua đó sẽ giúp các bạn học sinh kiểm tra kiến thức cũng như củng cố lại các kiến thức đã được học về phần Hình học lớp 9. Đồng thời đây cũng là tài liệu để các bạn học sinh có thể tham khảo và ôn luyện chuẩn bị cho kì thi vào 10 sắp tới.

Tổng hợp kiến thức Hình học lớp 9 được VnDoc chia sẻ trên đây. Hy vọng với tài liệu này sẽ giúp ích cho quý thấy cô có thêm tài liệu để ôn tập cho các em học sinh, các em học sinh ôn luyện chuẩn bị tốt cho các kì thi quan trọng sắp tới. Chúc các em học tốt, dưới đây là một số tài liệu Toán lớp 9, các em tham khảo nhé

.......................................................................

Ngoài Tổng hợp kiến thức Hình học lớp 9. Để giúp bạn đọc có thêm nhiều tài liệu học tập hơn nữa, VnDoc.com mời các bạn học sinh còn có thể tham khảo các đề thi học học kì 1 lớp 9, đề thi học học kì 2 lớp 9 các môn Toán, Văn, Anh, Hóa, Lý, Địa, Sinh mà chúng tôi đã sưu tầm và chọn lọc. Với đề thi lớp 9 này giúp các bạn rèn luyện thêm kỹ năng giải đề và làm bài tốt hơn. Chúc các bạn ôn thi tốt.

Để giúp bạn đọc có thể giải đáp được những thắc mắc và trả lời được những câu hỏi khó trong quá trình học tập. VnDoc.com mời bạn đọc cùng đặt câu hỏi tại mục hỏi đáp học tập của VnDoc. Chúng tôi sẽ hỗ trợ trả lời giải đáp thắc mắc của các bạn trong thời gian sớm nhất có thể nhé.