Trường hợp bằng nhau thứ ba của tam giác: góc - cạnh - góc
Chuyên đề Toán học lớp 7: Trường hợp bằng nhau thứ ba của tam giác: góc - cạnh - góc được VnDoc sưu tầm và giới thiệu tới các bạn học sinh cùng quý thầy cô tham khảo. Nội dung tài liệu sẽ giúp các bạn học sinh học tốt môn Toán học lớp 7 hiệu quả hơn. Mời các bạn tham khảo.
Bài Trường hợp bằng nhau thứ ba của tam giác: góc - cạnh - góc
A. Lý thuyết
1. Vẽ tam giác biết một cạnh và hai góc kề
Bài toán: Vẽ tam giác ABC biết BC = 4cm, ∠B = 60o, ∠C = 40o
• Vẽ đoạn thẳng BC = 4cm.
• Trên cùng một nửa mặt phẳng phẳng bờ BC, vẽ các tia Bx và Cy sao cho ∠CBx = 60o, ∠BCy = 40o.
Hai tia trên cắt nhau tại A, ta được tam giác ABC.
Lưu ý: Ta gọi góc B và góc C là hai góc kề cạnh BC. Khi nói một cạnh và hai góc kề, ta hiểu hai góc này là hai góc ở vị trí kề cạnh đó.
2. Trường hợp bằng nhau góc – cạnh – góc
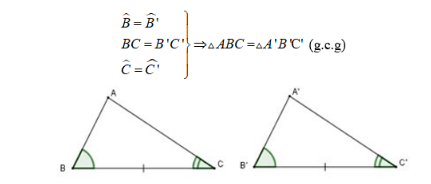
Nếu một cạnh và hai góc kề của tam giác này bằng một cạnh và hai góc kề của tam giác kia thì hai tam giác đó bằng nhau.
ΔABC và ΔA'B'C' có:
3. Hệ quả
• Hệ quả 1: Nếu một cạnh góc vuông và một góc nhọn kề cạnh ấy của tam giác vuông này bằng một cạnh góc vuông và một góc nhọn kề cạnh ấy của tam giác vuông kia thì hai tam giác vuông đó bằng nhau.
• Hệ quả 2: Nếu cạnh huyền và một góc nhọn của tam giác vuông này bằng cạnh huyền và một góc nhọn của tam giác vuông kia thì hai tam giác vuông đó bằng nhau.
Ví dụ:

B. Trắc nghiệm & Tự luận
I. Câu hỏi trắc nghiệm
Bài 1: Cho tam giác ABC và tam giác NPM có BC = PM; ∠B = ∠P. Cần điều kiện gì để tam gác ABC bằng tam giác NPM theo trường hợp góc – cạnh – góc?
A. ∠M = ∠A B. ∠A = ∠P C. ∠C = ∠M D. ∠A = ∠N
Xét tam giác ABC và tam giác NPM có BC = PM; ∠B = ∠P.
Để hai tam gác ABC bằng tam giác NPM theo trường hợp góc – cạnh – góc thì cần điều kiện là ∠C = ∠M
Chọn đáp án C.
Bài 2: Cho hai tam giác ABC và tam giác MNP có ∠A = ∠M, ∠B = ∠N. Cần điều kiện gì để hai tam giác ABC và tam giác MNP bằng nhau theo trường hợp góc - cạnh – góc?
A. AC = MP B. AB = MN C. BC = NP D. AC = MN
Xét hai tam giác ABC và tam giác MNP có ∠A = ∠M, ∠B = ∠N.
Để hai tam giác ABC và MNP bằng nhau cần điều kiện AB = MN theo trường hợp góc – cạnh – góc .
Chọn đáp án B.
Bài 3: Cho tam giác ABC và tam giác MNP có ∠B = ∠N = 90°; AC = MP, ∠C = ∠M. Phát biểu nào sau đây đúng?
A. ΔABC = ΔPMN
B. ΔACB = ΔPMN
C. ΔBAC = ΔMNP
D. ΔABC = ΔPNM
Xét tam giác ABC và tam giác MNP có: ∠B = ∠N = 90°; AC = MP, ∠C = ∠M
Suy ra: ΔABC = ΔPNM (g-c-g)
Chọn đáp án D.
Bài 4: Cho góc nhọn xOy, Oz là tia phân giác của góc đó. Qua điểm A thuộc tia Ox kẻ song song với Oy cắt Oz tại M. Qua M kẻ đường song song với Ox cắt Oy tại B. Chọn câu đúng
A. OA > OB; MA > MB
B. OA = OB; MA = MB
C. OA < OB; MA < MB
D. OA < OB; MA = MB


Bài 5: Cho đoạn thẳng AB, O là trung điểm của đoạn thẳng AB. Trên cùng một nửa mặt phẳng bờ AB vẽ các tia Ax, By vuông góc với AB. Gọi C là một điểm thuộc tia Ax. Đường vuông góc với OC tại O cắt tia By tại D. Khi đó
A. CD = AC + BD
B. CD = AC - BD
C. AC = DC + BD
D. AC = CD - BD


Xét tam giác DOC và tam giác DOK có
OC = OK
∠DOC = ∠DOK = 90°
OD là cạnh chung
⇒ ΔDOC = ΔDOK (g-c-g)
Suy ra CD = DK (cạnh tương ứng bằng nhau)
Ta có: DK = DB + BK mà AC = BK; CD = DK
Do đó: CD = AC + BD
Chọn đáp án A.
II. Bài tập tự luận
Bài 1: Cho ΔABC có ∠B = ∠C. Tia phân giác của góc B cắt AC tại D. Tia phân giác của góc C cắt AB tại E. So sánh độ dài đoạn thằng BD và CE.

Bài 2: Cho tam giác ABC (AB = AC) và I là trung điểm của đáy BC. Dựng tia Cx song song với tia BA sao cho hai tia BA và Cx nằm trong hai nửa mặt phẳng đối nhau có bờ là đường thẳng BC. Lấy một điểm D nào đó trên AB. Gọi E là một điểm nằm trên tia Cx sao cho BD = CE. Chứng minh rằng ba điểm D, I, E thẳng hàng.

Xét hai tam giác BID và CIE ta có:
BI = IC (I là trung điểm của BC)
∠IBD = ∠ICE (hai góc so le trong)
BD = CE (gt)
⇒ ΔBID = ΔCIE (c-g-c)
Nên ∠BID = ∠CIE (hai góc tương ứng bằng nhau)
Hai góc này bằng nhau, chiếm vị trí đối đỉnh, có hai cạnh tương ứng BI và CI nằm trên một đường thẳng.
Vậy D, I, E thẳng hàng
Trên đây VnDoc đã giới thiệu tới các bạn lý thuyết môn Toán học 7: Trường hợp bằng nhau thứ ba của tam giác: góc - cạnh - góc. Để có kết quả cao hơn trong học tập, VnDoc xin giới thiệu tới các bạn học sinh tài liệu Chuyên đề Toán học 7, Giải bài tập Toán lớp 7, Giải VBT Toán lớp 7 mà VnDoc tổng hợp và giới thiệu tới các bạn đọc