Tuyển tập 100 hệ phương trình luyện thi đại học
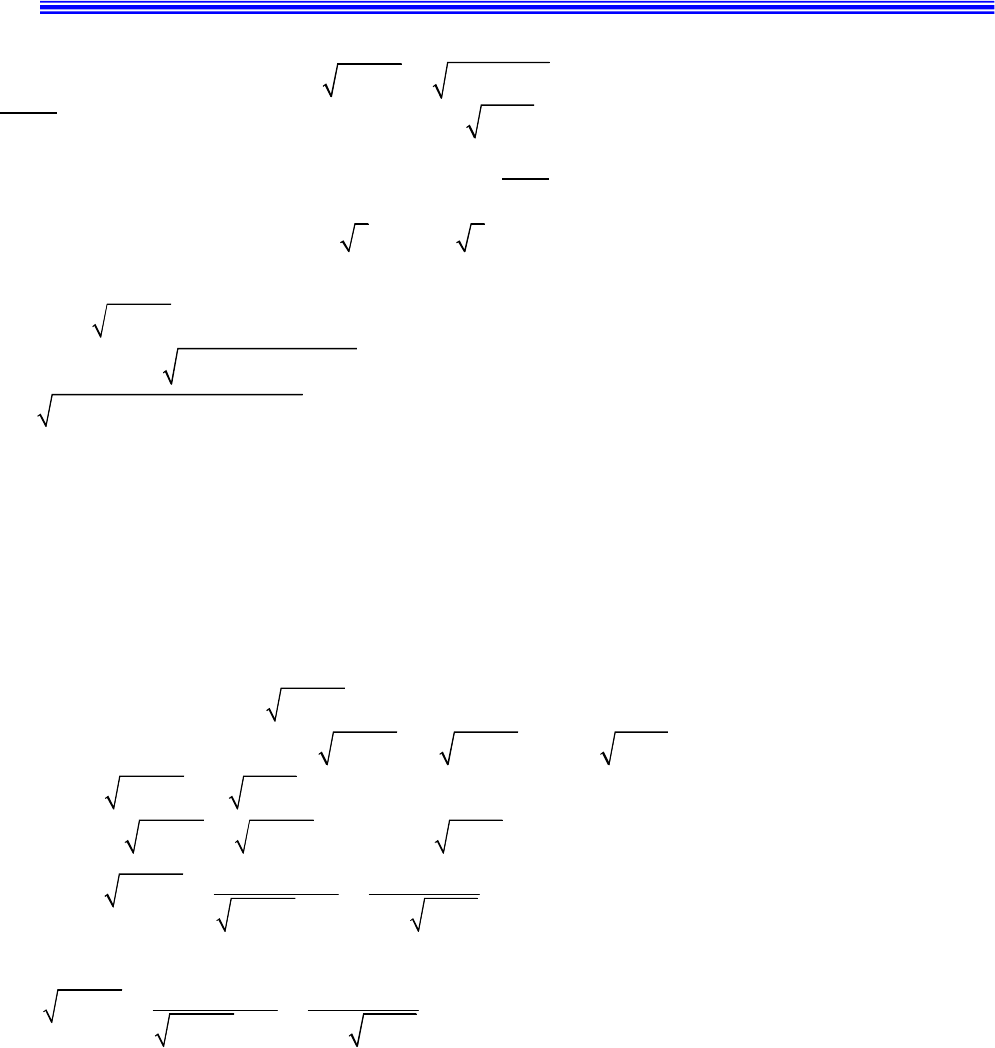
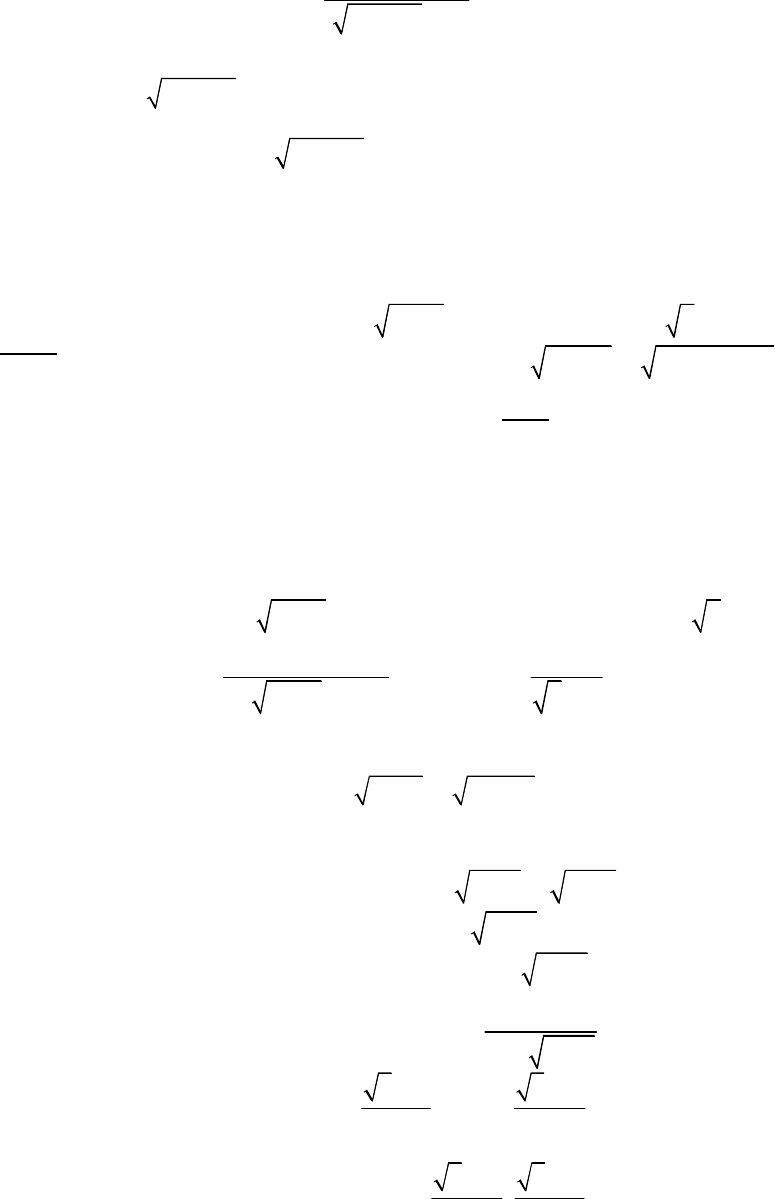
100 hệ phương trình luyện thi THPT Quốc gia
Tuyển tập 100 hệ phương trình luyện thi đại học được các giáo viên trường THPT Hùng Vương, Bình Phước biên soạn, là tài liệu luyện thi đại học môn Toán hay, tổng hợp nhiều dạng hệ phương trình hay cũng như các cách giải tổng hợp. Đây là tài liệu ôn thi THPT Quốc gia môn Toán, luyện thi đại học môn Toán hay và có chất lượng. Mời các bạn tham khảo.
Đề thi thử THPT Quốc gia môn Toán lần 1 năm 2016 trường THPT Chuyên Vĩnh Phúc
Đề thi thử THPT Quốc gia môn Toán lần 2 năm 2016 trường THPT Đào Duy Từ
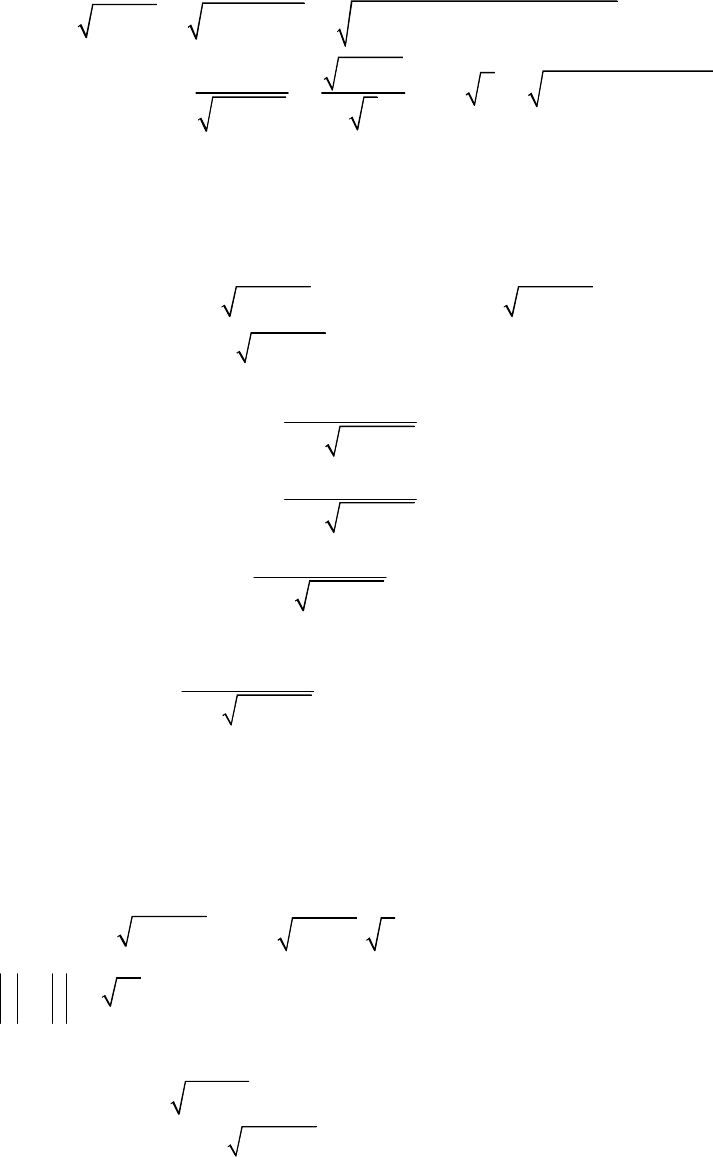
Các hệ phương trình thường gặp trong đề thi THPT Quốc Gia
NHÓM GIÁO VIÊN THỰC HIỆN:
1) PHẠM VĂN QUÝ
2) NGUYỄN VIẾT THANH
3) DOÃN TIẾN DŨNG
ĐƠN VỊ CÔNG TÁC: TRƯỜNG THPT HÙNG VƯƠNG, TX ĐỒNG XOÀI, TỈNH BÌNH PHƯỚC

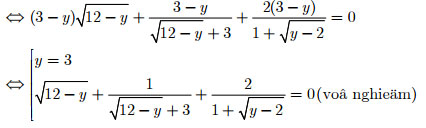
Vậy x = 3 và y = 3.
Cách 2:

<=> x = 3 => y = 3
Vậy x = 3 và y = 3.
Cách 3:
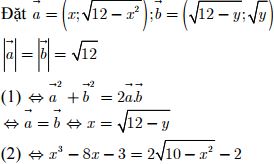

f'(x) < 0 ∀x => phương trình vô nghiệm
Vậy nghiệm của hệ phương trình trên: (3; 3).


Từ đó ta có các nghiệm (x; y) là: (1;2),(2;3),(1;3),(2;2).
Kết luận: Hệ phương trình có 4 nghiệm là: (1;2),(2;3),(1;3),(2;2).







