Chia đơn thức cho đơn thức
Chuyên đề Toán học lớp 8: Chia đơn thức cho đơn thức được VnDoc sưu tầm và giới thiệu tới các bạn học sinh cùng quý thầy cô tham khảo. Nội dung tài liệu sẽ giúp các bạn học sinh học tốt môn Toán học lớp 8 hiệu quả hơn. Mời các bạn tham khảo.
Chuyên đề: Chia đơn thức cho đơn thức
A. Lý thuyết
1. Đơn thức chia cho đơn thức
Với A và B là hai đơn thức, B≠0. Ta nói A chia hết cho B nếu tìm được một đơn thức Q sao cho A = B.Q.
Trong đó:
A là đơn thức bị chia.
B là đơn thức chia.
Q là đơn thức thương (hay gọi là thương)
Kí hiệu: Q = A : B
2. Quy tắc
Nhớ lại kiến thức cũ: Ở lớp 7 ta biết: Với x≠0; m, n ∈ N; m ≥ n thì:
xm : xn = xm - n nếu m>n
xm : xn = 1 nếu m=n
Quy tắc:
Muốn chia đơn thức A cho đơn thức B (trường hợp A chia hết cho B) ta làm như sau:
+ Chia hệ số của đơn thức A cho hệ số của đơn thức B.
+ Chia lũy thừa của từng biến trong A cho lũy thừa của cùng biến đó trong B.
+ Nhân các kết quả vừa tìm được với nhau.
Ví dụ: Thực hiện phép tính
a, (- 2)5:(- 2)3.
b, (xy2)4:(xy2)2
Hướng dẫn:
a) Ta có: (- 2)5:(- 2)3 = (- 2)5 - 3 = (- 2)2 = 4.
b) Ta có: (xy2)4:(xy2)2 = x4y8:x2y4 = x4 - 2.y8 - 4 = x2y4.
B. Trắc nghiệm & Tự luận
I. Bài tập trắc nghiệm
Bài 1: Kết quả nào sau đây đúng?
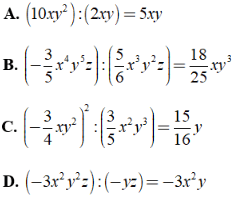
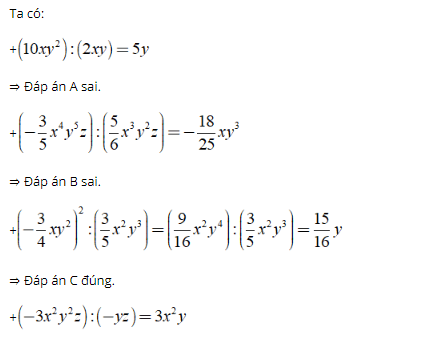
⇒ Đáp án D sai.
Chọn đáp án C.
Bài 2: Kết quả của phép tính (- 3)6:(- 2)3 là?
A. 729/8 B. 243/8 C. -729/8 D. -243/8
Ta có: (- 3)6:(- 2)3 = 36:(- 23) = 729:(- 8) = - 729/8.
Chọn đáp án C.
Bài 3: Giá trị của biểu thức A = (xy2)3:(xy)3 tại x= -1, y =1 là?
A. A= -1 B. A= 1 C. A= 0 D. A= 2
Ta có A = (xy2)3:(xy)3 = (x3y6):(x3y3) = y3.
Với x= -1, y =1 ta có A = 13 = 1.
Chọn đáp án B.
II. Bài tập tự luận
Bài 1: Tính giá trị của các biểu thức sau
a) P = 12x4y2:(- 9xy2) tại x= -3, y= 1,005.
b) Q = 3x4y3:2xy2 tại x= 2, y= 1.
Hướng dẫn:
a) Ta có P = 12x4y2:(- 9xy2) = 1/2 - 9x4 - 1y2 - 2 = - 4/3x3
Với x= -3, y= 1,005 ta có P = - 4/3(- 3)3 = 36.
Vậy P = 36
b) Ta có Q = 3x4y3:2xy2 = 3/2x4 - 1y3 - 2 = 3/2x3y.
Với x= 2, y= 1 ta có Q = 3/2( 2 )3.1 = 12.
Vậy Q = 12
Bài 2: Chứng mình rằng giá trị của biểu thức sau không phụ thuộc vào giá trị của biến y (x≠0; y≠0) với biểu thức đó là A = 2/3x2y3:(- 1/3xy) + 2x(y - 1)(y + 1)
Hướng dẫn:
Ta có A = 2/3x2y3:(- 1/3xy) + 2x(y - 1)(y + 1) = - 2x2 - 1y3 - 1 + 2x(y - 1)(y + 1)
= - 2xy2 + 2x(y2 - 1) = - 2xy2 + 2xy2 - 2x = - 2x
⇒ Giá trị của biểu thức A không phụ thuộc vào biến y
Trên đây VnDoc đã giới thiệu tới các bạn lý thuyết môn Toán học 8: Chia đơn thức cho đơn thức. Để có kết quả cao hơn trong học tập, VnDoc xin giới thiệu tới các bạn học sinh tài liệu Chuyên đề Toán học 8, Giải bài tập Toán lớp 8, Giải VBT Toán lớp 8 mà VnDoc tổng hợp và giới thiệu tới các bạn đọc








