Hình thang
Chuyên đề Toán học lớp 8: Hình thang được VnDoc sưu tầm và giới thiệu tới các bạn học sinh cùng quý thầy cô tham khảo. Nội dung tài liệu sẽ giúp các bạn học sinh học tốt môn Toán học lớp 8 hiệu quả hơn. Mời các bạn tham khảo.
Chuyên đề: Hình thang
A. Lý thuyết
1. Định nghĩa
Hình thang là tứ giác có hai cạnh đối song song.
Hai cạnh song song gọi là hai đáy.
Hai cạnh còn lại gọi là hai cạnh bên.
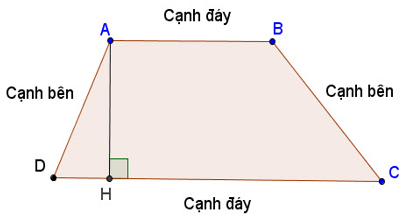
Gọi AH là đường vuông góc kẻ từ A đến đường thẳng CD, đoạn thẳng AH được gọi là đường cao của hình thang
Nhận xét:
Nếu một hình thang có hai cạnh bên song song thì hai canh bên bằng nhau, hai cạnh đấy bằng nhau.
Nếu một hình thang có hai cạnh đáy bằng nhau thì hai cạnh bên song song và bằng nhau.
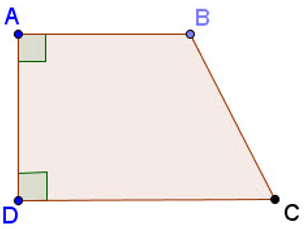
2. Hình thang vuông
Định nghĩa: Hình thang vuông là hình thang có một góc vuông
Dấu hiệu nhận biết: Hình thang có một góc vuông là hình thang vuông
3. Ví dụ minh họa
Ví dụ: Cho hình thang ABCD ( AB//CD ) có Aˆ - Dˆ = 300,Bˆ = 2Cˆ. Tính các góc của hình thang
Hướng dẫn:
Trong hình thang ABCD có Aˆ + Bˆ + Cˆ + Dˆ = 3600. ( 1 )
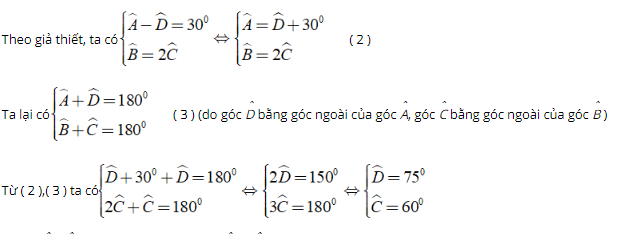
Khi đó Aˆ = Dˆ + 300 = 750 + 300 = 1250; Bˆ = 2Cˆ = 1200.
B. Trắc nghiệm & Tự luận
I. Bài tập trắc nghiệm
Bài 1: Chọn câu đúng trong các câu sau:
A. Hình thang có ba góc tù, một góc nhọn.
B. Hình thang có ba góc vuông, một góc nhọn.
C. Hình thang có ba góc nhọn, một góc tù.
D. Hình thanh có nhiều nhất hai góc nhọn và nhiều nhất hai góc tù.
Ta có tổng các góc của hình thang bằng 3600.
+ Hình thang có ba góc tù, một góc nhọn.
Ví dụ: Hình thang có 3 góc tù là 1000,1200,1350 và 1 góc nhọn là 600.
⇒ Tổng 4 góc của hình thang bằng 1000 + 1200 + 1350 + 600 = 4150 > 3600
⇒ Không tồn tại hình thang có ba góc tù, một góc nhọn. ⇒ Đáp án A sai
+ Hình thang có ba góc vuông, một góc nhọn.
Ví dụ: Hình thang có 3 góc bằng 900 và một góc nhọn bằng 650.
⇒ Tổng 4 góc của hình thang bằng 900 + 900 + 900 + 650 = 3350 < 3600
⇒ Không tồn tại hình thang ba góc vuông, một góc nhọn. ⇒ Đáp án B sai.
+ Hình thang có ba góc nhọn, một góc tù.
Ví dụ: Hình thang có ba góc nhọn là 450,750,800, một góc tù là 1600
⇒ Tổng 4 góc của hình thang bằng 450 + 750 + 800 + 1600 = 3600
⇒ Tồn tại Hình thang có ba góc nhọn, một góc tù. ⇒ Đáp án C đúng
⇒ Hình thang có nhiều nhất là 3 góc nhọn. ⇒ Đáp án D sai.
Chọn đáp án C.
Bài 2: Một hình thang có một cặp góc đối là 1250 và 750, cặp góc đối còn lại của hình thang đó là?
A. 1050, 550 B. 1050, 450 C. 1150, 550 D. 1150, 650
Tổng bốn góc của hình thang bằng 3600.
Theo giả thiết ta có một cặp góc đối là 1250 và 750
⇒ Tổng số đo góc của cặp góc đối còn lại là 1600.
Xét đáp án ta có cặp 1050,550 thỏa mãn.
Chọn đáp án A.
Bài 3: Hình thang ABCD có Cˆ + Dˆ = 1500. Khi đó Aˆ + Bˆ = ?
A. 2200 B. 2100 C. 2000 D. 1900
Tổng bốn góc của hình thang bằng 3600.
Khi đó ta có: Aˆ + Bˆ + Cˆ + Dˆ = 3600 ⇒ Aˆ + Bˆ = 3600 - (Cˆ + Dˆ)
⇒ Aˆ + Bˆ = 3600 - 1500 = 2100.
Chọn đáp án B.
Bài 4: Cho hình thang ABCD trong đó có Aˆ = 1200, Bˆ = 600, Dˆ = 1350 thì số đo của góc Cˆ = ?
A. 550 B. 450 C. 500 D. 600
Tổng bốn góc của hình thang bằng 3600.
Khi đó ta có: Aˆ + Bˆ + Cˆ + Dˆ = 3600 ⇒ Cˆ = 3600 - (Aˆ + Bˆ + Dˆ)
⇒ Cˆ = 3600 - (1200 + 600 + 1350) = 450.
Chọn đáp án B.
II. Bài tập tự luận
Bài 1: Hình thang vuông ABCD có Aˆ = Dˆ = 900; AB = AD = 3cm;CD = 6cm. Tính số đo góc B và C của hình thang?
Hướng dẫn:
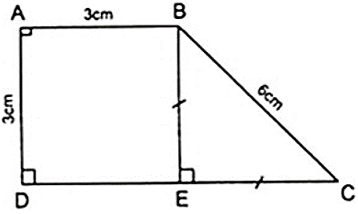
Kẻ BE ⊥ CD thì AD//BE do cùng vuông góc với CD
+ Hình thang ABED có cặp cạnh bên song song là hình bình hành.
Áp dụng tính chất của hình bình hành ta có
AD = BE = 3cm
Xét Δ BEC vuông tại E có 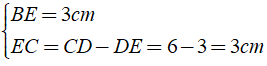
⇒ Δ BEC là tam giác vuông cân tại E.
Khi đó ta có: Cˆ = 450 và ABCˆ = 900 + 450 = 1350.
Bài 2: Cho hình thang ABCD( AB//CD ), hai đường phân giác của góc C và D cắt nhau tại I thuộc đáy AB. Chứng minh rằng tổng độ dài hai cạnh bên bằng độ dài của đáy AB của hình thang
Hướng dẫn:
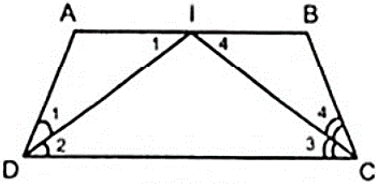
Áp dụng tính chất so le của AB//CD và giả thiết ta có:
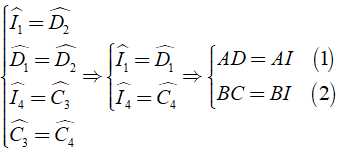
(vì trong một tam giác đối diện với hai góc bằng nhau là hai cạnh bằng nhau)
Cộng vế theo vế của ( 1 ) và ( 2 ) ta được: AD + BC = AB
Điều đó chứng tỏ tổng độ dài hai cạnh bên bằng độ dài của đáy AB của hình thang
Trên đây VnDoc đã giới thiệu tới các bạn lý thuyết môn Toán học 8: Hình thang . Để có kết quả cao hơn trong học tập, VnDoc xin giới thiệu tới các bạn học sinh tài liệu Chuyên đề Toán học 8, Giải bài tập Toán lớp 8, Giải VBT Toán lớp 8 mà VnDoc tổng hợp và giới thiệu tới các bạn đọc







