Lý thuyết Hình học 10 chương 1 bài 1

Lý thuyết hình học 10

Mời quý thầy cô cùng các em học sinh tham khảo tài liệu Lý thuyết Hình học 10 chương 1 bài 1 được VnDoc biên soạn, trình bày khoa học, với toàn bộ nội dung trọng tâm của bài học được đúc kết nhằm hỗ trợ quá trình giảng dạy và học tập môn Toán lớp 10.

Hình học 10 - Lý thuyết Các định nghĩa

1. Định nghĩa, sự xác định vectơ.

- Vectơ là một đoạn thẳng có định hướng, nghĩa là trong hai điểm mút của đoạn thẳng, đã chỉ rõ điểm nào là điểm đầu (gốc), điểm nào là điểm cuối (ngọn). Vectơ có điểm đầu A, điểm cuối B được kí hiệu là \(\underset{AB}{\rightarrow}\).

• Nếu không quan tâm đến điểm đầu, điểm cuối của vectơ, ta có thể kí hiệu vectơ là \(\underset{a}{\rightarrow}\), \(\underset{b}{\rightarrow}\), \(\underset{x}{\rightarrow}\)…
• Một vectơ hoàn toàn được xác định khi biết điểm đầu và điểm cuối của nó.

Lưu ý: Với hai điểm phân biệt A và B ta chỉ có một đoạn thẳng (AB hoặc BA), nhưng có hai vectơ khác nhau là \(\underset{AB}{\rightarrow}\), \(\underset{BA}{\rightarrow}\).

- Độ dài của đoạn thẳng AB là độ dài (hay môđun) của vectơ \(\underset{AB}{\rightarrow}\), kí hiệu là |\(\underset{AB}{\rightarrow}\)|. Đương nhiên |\(\underset{AB}{\rightarrow}\)|=|\(\underset{BA}{\rightarrow}\)|.

- Vectơ – không là vectơ có điểm đầu và điểm cuối trùng nhau. Vectơ – không được kí hiệu là \(\underset{0}{\rightarrow}\). Ta có \(\underset{AA}{\rightarrow}\) = \(\underset{BB}{\rightarrow}\) = \(\underset{0}{\rightarrow}\); vectơ \(\underset{0}{\rightarrow}\) có độ dài bằng 0.

2. Hai vectơ cùng phương, cùng hướng.

- Giá của một vectơ khác 0→ là đường thẳng của điểm đầu và điểm cuối của vectơ đó.

- Hai vectơ được gọi là cùng phương nếu giá trị của chúng song song hoặc trùng nhau. Trên hình a) ta có các vectơ \(\underset{AB}{\rightarrow}\), \(\underset{CD}{\rightarrow}\), \(\underset{EF}{\rightarrow}\) cùng phương. Trên hình b) ta có \(\underset{AB}{\rightarrow}\) và \(\underset{MN}{\rightarrow}\) cùng phương, còn \(\underset{AB}{\rightarrow}\) và \(\underset{MN}{\rightarrow}\) không cùng phương.

- Hai vectơ cùng phương có thể cùng hướng hoặc ngược hướng. Chẳng hạn \(\underset{AB}{\rightarrow}\) và \(\underset{CD}{\rightarrow}\) cùng hướng, \(\underset{AB}{\rightarrow}\) và \(\underset{EF}{\rightarrow}\) ngược hướng (h.a)

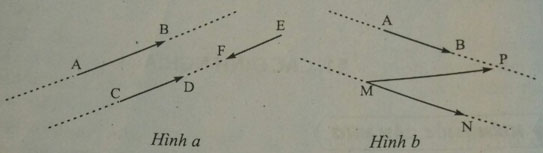
Lưu ý: Khi nói hai vectơ cùng hướng hay ngược hướng thì chúng đã cùng phương. Vectơ \(\underset{0}{\rightarrow}\) cùng phương, cùng hướng với mọi vectơ.

3. Hai vectơ bằng nhau. Đối nhau.

- Hai vectơ gọi là bằng nhau nếu chúng có cùng hướng và cùng độ dài.

- Hai vectơ gọi là đối nhau nếu chúng ngược hướng và cùng độ dài.

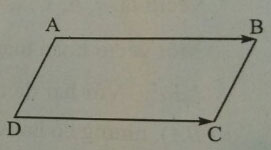
Chẳng hạn, nếu ABCD là hình bình hành thì \(\underset{AB}{\rightarrow}\) = \(\underset{DC}{\rightarrow}\) và \(\underset{AD}{\rightarrow}\) = \(\underset{BC}{\rightarrow}\), \(\underset{AB}{\rightarrow}\) và \(\underset{CD}{\rightarrow}\) là hai vectơ đối nhau, ta viết \(\underset{AB}{\rightarrow}\) = -\(\underset{CD}{\rightarrow}\). Hiển nhiên \(\underset{AB}{\rightarrow}\) và \(\underset{BA}{\rightarrow}\) là vectơ đối nhau.

4. Các hệ quả.

a) Cho hai vectơ \(\underset{AM}{\rightarrow}\) và \(\underset{BN}{\rightarrow}\) cùng phương nhưng không nằm trên một đường thẳng. Khi đó:

- \(\underset{AM}{\rightarrow}\) và \(\underset{BN}{\rightarrow}\) cùng hướng khi và chỉ khi M, N nằm cùng phía đối với đường thẳng AB (hình a).

- \(\underset{AM}{\rightarrow}\) và \(\underset{BN}{\rightarrow}\) ngược hướng khi và chỉ khi M, N nằm khác phía đối với đường thẳng AB (hình b).

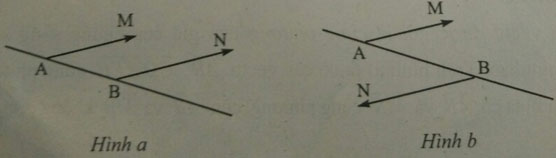
b) Hai vectơ cùng phương với vectơ thứ ba (khác \(\underset{0}{\rightarrow}\)) thì cùng phương với nhau.

Hai vectơ cùng hướng với vectơ thứ ba (khác \(\underset{0}{\rightarrow}\)) thì cùng hướng với nhau.

c) Cho ba vectơ \(\underset{a}{\rightarrow}\), \(\underset{b}{\rightarrow}\), \(\underset{c}{\rightarrow}\) có cùng phương. Khi đó có ít nhất hai vectơ trong chúng cùng hướng.

d) Nếu một vectơ có hai phương khác nhau thì nó là vectơ – không.