Lý thuyết Hình học 10 chương 1 bài 2

Lý thuyết hình học 10

Lý thuyết Hình học 10 chương 1 bài 2 là tài liệu tham khảo hữu ích do VnDoc biên soạn, với toàn bộ nội dung lý thuyết trọng tâm của bài học được tổng hợp, hỗ trợ quá trình dạy và học môn Toán lớp 10 đạt kết quả cao.

Hình học 10 - Lý thuyết Tổng và hiệu của hai vectơ

1. Tổng của hai vectơ.

Cho hai vectơ $\underset{a}{\to }$ và $\underset{b}{\to }$. Từ điểm O bất kì ta dựng $\underset{OA}{\to }$ = $\underset{a}{\to }$, $\underset{AB}{\to }$ = $\underset{b}{\to }$. Vectơ $\underset{OB}{\to }$ được gọi là tổng của hai vectơ $\underset{a}{\to }$ và $\underset{b}{\to }$, kí hiệu là $\underset{a}{\to }$ + $\underset{b}{\to }$.

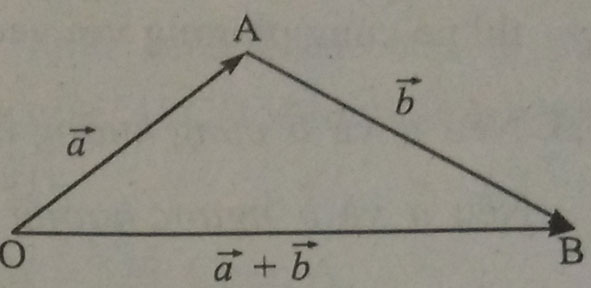
- Quy tắc ba điểm:

Với ba điểm A, B, C bất kì ta luôn có:

$\underset{AB}{\to }$ + $\underset{BC}{\to }$ = $\underset{AC}{\to }$ (1)

- Quy tắc hình bình hành

Trong hình bình hành ABCD ta luôn có:

$\underset{HB}{\to }$ + $\underset{HB}{\to }$ = $\underset{HB}{\to }$ (2)

2. Phép cộng có các tình chất.

3. Vectơ đối của vectơ $\underset{a}{\to }$ là vectơ ngược hướng và có cùng độ dài với vectơ $\underset{a}{\to }$, kí hiệu là -$\underset{a}{\to }$. Ta có $\underset{a}{\to }$ + (-$\underset{a}{\to }$) = 0→. Đương nhiên $\underset{BA}{\to }$ = -$\underset{AB}{\to }$

4. Hiệu của hai vectơ $\underset{a}{\to }$ và $\underset{b}{\to }$, kí hiệu là $\underset{a}{\to }$ - $\underset{b}{\to }$, là tổng của vectơ $\underset{a}{\to }$ và vectơ đối của vectơ $\underset{b}{\to }$, tức là $\underset{a}{\to }$ - $\underset{b}{\to }$ = $\underset{a}{\to }$ + (-$\underset{b}{\to }$)

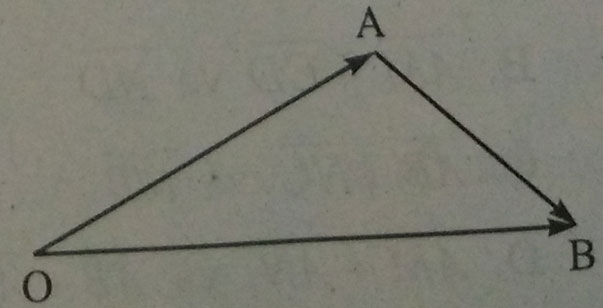
Quy tắc ba điểm đối với phép trừ:

Với ba điểm O, A, B bất kì ta luôn có

$\underset{AB}{\to }$ = $\underset{OB}{\to }$ - $\underset{OA}{\to }$ (3)

5. Các hệ quả.

5.1. Mở rộng quy tắc ba điểm: Cho n điểm bất kì A₁, A₂,…, A_n (n > 2). Ta có

5.2. Nếu vectơ $\underset{a}{\to }$ + $\underset{b}{\to }$ (hoặc $\underset{a}{\to }$ - $\underset{b}{\to }$) cùng phương với một trong hai vectơ $\underset{a}{\to }$ hoặc $\underset{b}{\to }$ thì nó cùng phương với vectơ còn lại.

5.3. Nếu $\underset{a}{\to }$ và $\underset{b}{\to }$ cùng hướng thì |$\underset{a}{\to }$ + $\underset{b}{\to }$|=|$\underset{a}{\to }$|+|$\underset{b}{\to }$|

Nếu $\underset{a}{\to }$ và $\underset{b}{\to }$ ngược hướng thì |$\underset{a}{\to }$ + $\underset{b}{\to }$|=|(|$\underset{a}{\to }$|+|$\underset{b}{\to }$|)| (xem Ví dụ 5)