Đề thi học sinh giỏi giải toán trên máy tính cầm tay tỉnh Thanh Hóa năm 2011 môn Vật lí lớp 12 - Có đáp án

Để chuẩn bị cho kỳ thi chọn học sinh giỏi, Vndoc.com xin giới thiệu đến các bạn: Đề thi học sinh giỏi giải toán trên máy tính cầm tay tỉnh Thanh Hóa năm 2011 môn Vật lí lớp 12 - Có đáp án.

Đề thi học sinh giỏi môn Vật lí:

MÔN THI: VẬT LÍ
Thời gian làm bài: 150 phút (không kể thời gian giao đề)
--------------------------------------------------------------------------------

Câu 1: (2 điểm)

Tại thành phố Thanh Hoá, chu kì dao động của con lắc đơn chiều dài (l₁ + l₂) đo được là T₊ = 2,3s. Còn chu kì dao động của con lắc đơn chiều dài (l₁ - l₂) đo được là T_- = 0,9s. Hãy xác định chu kì dao động của các con lắc đơn lần lượt có chiều dài l₁ và l₂ tại thành phố Thanh Hoá. Kết quả tìm được có phụ thuộc vào gia tốc trọng trường hay không?

Câu 2: (2 điểm)

Cường độ âm thanh nhỏ nhất mà một nguời bình thường có thể nghe thấy ứng với tần số 10³ hz là I₀ = 10^-12 W/m². Bỏ qua mất mát năng lượng cho môi trường.

a) Hỏi một người bình thường đứng ở vị trí M cách xa nguồn O phát âm thanh tần số 10³ hz, công suất P = 5W một khoảng OM như thế nào thì vẫn còn nghe thấy âm thanh của nguồn phát ra?

b) Tính mức cường độ âm tại vị trí chính giữa của OM nói trên

Câu 3: (2 điểm)

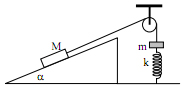
Một con lắc lò xo khối lượng m = 1kg và độ cứng k = 250 N/m được nối với vật khối lượng M = 4kg nằm trên mặt phẳng nghiêng có góc nghiêng α = 20^o nhờ một sợi dây mảnh vắt qua ròng ròng khối lượng không đáng kể (hình vẽ). Bỏ qua ma sát giữa M với mặt phẳng nghiêng. Hãy xác định độ giãn của lò xo khi hệ nằm cân bằng và xác định chu kì của hệ khi M thực hiện dao động nhỏ trên mặt phẳng nghiêng

Câu 4: (2 điểm)

Một chất điểm chuyển động tròn đều với bán kính quĩ đạo là 3,5cm, thời gian chuyển động hết một vòng là 12s. Chọn mốc thời gian là lúc chất điểm ở gần trục Ox nhất và gốc toạ độ là vị trí trên trục Ox gần quĩ đạo nhất. Hãy viết phương trình hình chiếu vuông góc của chất điểm lên trục Ox đồng phẳng với quĩ đạo chuyển động và xác định vị trí của vết chiếu tại thời điểm t = 100s

Câu 5: (2 điểm)

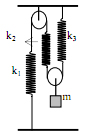
Cho hình vẽ dưới đây. Bỏ qua ma sát, khối lượng của các ròng rọc và dây nối. Các sợi dây dây đều mềm, mảnh, không giãn và luôn thẳng đứng. Tính độ cứng tương đương của hệ. Cho biết k₁ = 10 N/m; k₂ = 15 N/m; k₃ = 25 N/m.

Câu 6: (2 điểm)

Cho mạch điện xoay chiều hình bên. Biết R = 100Ω; ZC = 120Ω; cuộn dây thuần cảm ZL= 20Ω; uAB = 100sqrt(2)cos100πt (V). Tính điện lượng phóng qua tiết diện dây dẫn trong 1/8 chu kì

Câu 7: (2 điểm)

Trong mạch điện hình bên cuộn dây là thuần cảm. Khi K mở thì dòng điện là i₁ còn khi K đóng thì dòng điện là i₂. Biết rằng i₁ và i₂ khác pha nhau và I₁ = 2I₂. Tìm hệ số cống suất cosφ1 của mạch lúc K mở và tìm giá trị của φ1.

Câu 8: (2 điểm)

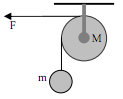
Một ròng rọc có bán kính R = 5cm, khối lượng M = 2kg, có thể quay không ma sát quanh một trục nằm ngang. Cuốn đầu một sợi dây mảnh, nhẹ vào ròng rọc và buộc đầu tự do vào hòn bi m = 3kg. Hòn bi cách mặt đất 2m (hình vẽ). Thả nhẹ hòn bi cho rơi xuống. Bỏ qua sức cản không khí. Hỏi khi hòn bi tiếp đất thì ròng rọc quay với tốc độ góc là bao nhiêu ?

Câu 9: (2 điểm)

Một con lắc lò xo có chiều dài tự nhiên l₀ = 10 cm và khối lượng là m = 100 g. Con lắc có đầu phía trên cố định, đầu dưới có thể trượt trên mặt phẳng nghiêng với góc nghiêng α₁ = 60^o (hình vẽ). Chiều dài con lắc khi nằm cân bằng trên mặt phẳng nghiêng là l₁ = 12,16 cm.

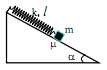
a) Bỏ qua ma sát. Tính chiều dài l₂ của con lắc nếu góc nghiêng giảm xuống đến α₂ = 30^o?

b) Thực tế giữa m và mặt phẳng nghiêng có ma sát nên sau 10 chu kì dao động trên mặt phẳng nghiêng α₁ thì biên độ đã giảm đi 1 cm. Tìm hệ số ma sát μ.

Câu 10: (2 điểm)

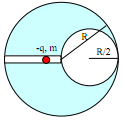
Bên trong một quả cầu đặc, điện môi tích điện đều, bán kính R, có một khoang cầu bán kính R/2 với tâm cách tâm quả cầu một khoảng bằng R/2. Hình bên. Điện tích toàn phần của quả cầu là Q. Dọc theo đường nối tâm quả cầu và khoang rỗng có một khe hẹp, bán kính nhỏ, bên trong có điện tích điểm (-q) khối lượng m. Xác định vị trí cân bằng của quả cầu nhỏ, coi rằng ma sát không đáng kể.