Đề thi vào lớp 10 THPT môn Toán của thành phố Hà Nội từ năm 1988 đến 2013
Đề thi vào lớp 10 môn Toán
Đề thi vào lớp 10 THPT môn Toán của thành phố Hà Nội từ năm 1988 đến năm 2013 là tài liệu tổng hợp đề thi vào lớp 10 THPT môn Toán các năm, có lời giải gợi ý. Đây là tài liệu rất cần thiết dành cho học sinh và thầy cô giáo tham khảo trước khi bước vào kì thi vào lớp 10 THPT, ôn thi vào lớp 10 môn Toán hiệu quả. Mời thầy cô và các bạn cùng tham khảo.
Tuyển tập đề thi vào lớp 10 môn Ngữ văn các tỉnh năm học 2014 - 2015
ĐỀ THI TUYỂN SINH LỚP 10 THPT HÀ NỘI
Năm học: 2011 – 2012
ĐỀ CHÍNH THỨC MÔN: TOÁN
Thời gian làm bài: 120 phút
Bài I (2,5 điểm)
| Cho | 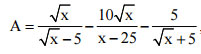 |
Với x ≥ 0 và x ≠ 25. |
- Rút gọn biểu thức A.
- Tìm giá trị của A khi x = 9.
- Tìm x để A < 1/3.
Bài II (2,5 điểm)
Giải bài toán sau bằng cách lập phương trình hoặc hệ phương trình:
Một đội xe theo kế hoạch chở hết 140 tấn hàng trong một số ngày quy định. Do mỗi ngày đội đó chở vượt mức 5 tấn nên đội đã hoàn thành kế hoạch sớm hơn thời gian quy định 1 ngày và chở thêm được 10 tấn. Hỏi theo kế hoạch đội xe chở hàng hết bao nhiêu ngày?
Bài III (1,0 điểm)
Cho parabol (P): y = x2 và đường thẳng (d) : y = 2x – m2 + 9.
- Tìm tọa độ các giao điểm của parabol (P) và đường thẳng (d) khi m = 1.
- Tìm m để đường thẳng (d) cắt parabol (P) tại hai điểm nằm về hai phía của trục tung.
Bài IV (3,5 điểm)
Cho đường tròn tâm O, đường kính AB = 2R. Gọi d1 và d2 lần lượt là hai tiếp tuyến của đường tròn (O) tại hai điểm A và B. Gọi I là trung điểm của OA và E là điểm thuộc đường tròn (O) (E không trùng với A và B). Đường thẳng d đi qua điểm E và vuông góc với EI cắt hai đường thẳng d1, d2 lần lượt tại M, N.
- Chứng minh AMEI là tứ giác nội tiếp.
- Chứng minh góc ENI = góc EBI và góc MIN = 900
- Chứng minh AM.BN = AI.BI.
- Gọi F là điểm chính giữa của cung AB không chứa E của đường tròn (O). Hãy tính diện tích của tam giác MIN theo R khi ba điểm E, I, F thẳng hàng.
Bài V (0,5 điểm)
Với x > 0, tìm giá trị nhỏ nhất của biểu thức: M = 4x2 - 3x + 1/4x + 2011.
Đề thi - Đáp án thi tuyển sinh lớp 10 THPT tỉnh Bình Định năm 2014 - 2015
Tổng hợp đề thi vào lớp 10 môn Tiếng Anh các tỉnh
Đề thi thử vào lớp 10 môn Toán thành phố Hà Nội năm học 2015-2016
Đáp án đề thi vào lớp 10 môn Toán
Bài I: (2,5 điểm) Với x ≥ 0 và x ≠ 25 ta có
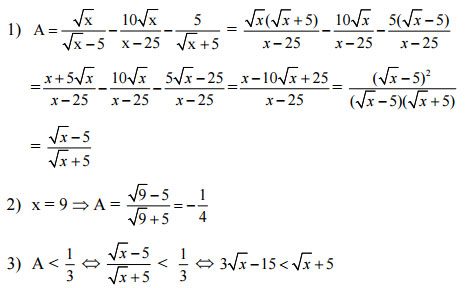
↔ 2√x < 20 ↔ √x < 10 ↔ 0 ≤ x < 100
Bài II: (2,5 điểm)
Cách 1: Gọi x (ngày) (x ϵ N*) là số ngày theo kế hoạch đội xe chở hết hàng
Theo đề bài ta có: (140/x + 5)(x - 1) = 140 + 10
↔ 140x + 5x2 – 140/x - 5 = 150 ↔ 5x2 – 15x – 140 = 0 ↔ x = 7 hay x = -4 (loại)
Vậy đội xe chở hết hàng theo kế hoạch trong 7 ngày.





