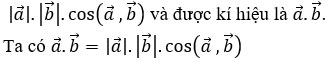Giao diện mới của VnDoc Pro: Dễ sử dụng hơn - chỉ tập trung vào lớp bạn quan tâm. Vui lòng chọn lớp mà bạn quan tâm: Lưu và trải nghiệm

VnDoc.com

Lý thuyết Hình học 10 chương 2 bài 2

Lý thuyết Tích vô hướng của hai vectơ

1 955

Lý thuyết hình học 10

Mời quý thầy cô cùng các em học sinh tham khảo tài liệu Lý thuyết Hình học 10 chương 2 bài 2 do VnDoc sưu tầm và biên soạn. Tài liệu bao gồm toàn bộ nội dung lý thuyết trọng tâm của bài học, được trình bày khoa học nhằm hỗ trợ quá trình dạy và học môn Toán đạt chất lượng.

Lý thuyết Hình học 10 chương 2 bài 1

Lý thuyết Hình học 10 chương 2 bài 3

Hình học 10 - Lý thuyết Tích vô hướng của hai vectơ

1. Tích vô hướng của hai vectơ

- Cho hai vectơ $\underset{a}{\rightarrow}$ , $\underset{b}{\rightarrow}$ ≠ $\underset{0}{\rightarrow}$ . Tích vô hướng của hai vectơ $\underset{a}{\rightarrow}$ , $\underset{b}{\rightarrow}$ là một số được xác định bởi công thức:

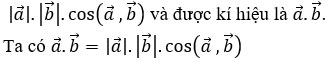
- Khi một trong hai vectơ $\underset{a}{\rightarrow}$ , $\underset{b}{\rightarrow}$ bằng 0 thì $\underset{a}{\rightarrow}$ . $\underset{a}{\rightarrow}$ = 0

2. Hai vectơ vuông góc

Hai vectơ $\underset{a}{\rightarrow}$ , $\underset{b}{\rightarrow}$ ≠ $\underset{0}{\rightarrow}$ vuông góc với nhau khi và chỉ khi $\underset{a}{\rightarrow}$ . $\underset{b}{\rightarrow}$ = 0

3. Độ dài của vectơ và bình phương vô hướng của vectơ

- Bình phương vô hướng

Kí hiệu $\underset{a}{\rightarrow}$ ²= | $\underset{a}{\rightarrow}$ |². Biểu thức $\underset{a}{\rightarrow}$ ² là một số thực không âm và được gọi là bình phương vô hướng của vectơ $\underset{a}{\rightarrow}$ .

- Liên hệ độ dài vectơ và bình phương vô hướng | $\underset{a}{\rightarrow}$ | = √( $\underset{a}{\rightarrow}$ ²)

4. Một số tính chất của tích vô hướng

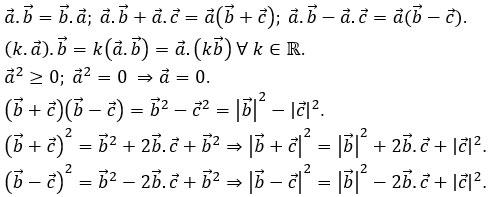
5. Biểu thức tọa độ của tích vô hướng

Nếu $\underset{a}{\rightarrow}$ = (x₁; y₁ ), $\underset{b}{\rightarrow}$ = (x₂; y₂ ) thì $\underset{a}{\rightarrow}$ . $\underset{b}{\rightarrow}$ = x₁.x₂+ y₁.y₂

6. Độ dài của vectơ và khoảng cách giữa hai điểm

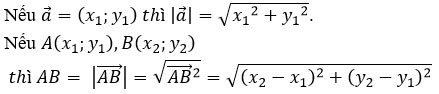
7. Cosin của góc giữa hai vectơ $\underset{a}{\rightarrow}$ , $\underset{b}{\rightarrow}$ ≠ $\underset{0}{\rightarrow}$

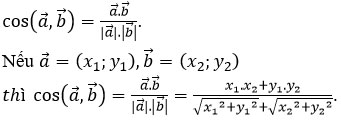
8. Chú ý

Khi giải bài tập trắc nghiệm, học sinh cần chú ý thêm cả kĩ năng loại trừ phương án. Trong nội dung tích vô hướng, học sinh cần ghi nhớ $\underset{a}{\rightarrow}$ . $\underset{b}{\rightarrow}$ nhận giá trị là một số thực.

Lý thuyết hình học 10

Đánh giá bài viết

1 955