Lý thuyết Hình học 10 chương 2 bài 1

Lý thuyết Giá trị lượng giác của một góc bất kì từ 0 đến 180

Lý thuyết hình học 10

Lý thuyết Hình học 10 chương 2 bài 1 với phần tóm tắt nội dung trọng tâm bài học, hỗ trợ quá trình giảng dạy và học tập môn Toán lớp 10 đạt chất lượng cao. Mời các thầy cô cùng học sinh tham khảo!

Lý thuyết Hình học 10 chương 2 bài 2

Lý thuyết Hình học 10 chương 1 bài 4

Hình học 10 - Lý thuyết Giá trị lượng giác của một góc bất kì từ 0 đến 180

1. Với mỗi góc α (0^o ≤ α ≤ 180^o) ta xác định được một điểm M trên nửa đường tròn lượng giác sao cho góc xOM = α. Tung độ của điểm M là sin của góc α, kí hiệu là sin α. Hoành độ của M là côsin của góc α, kí hiệu là cos α

Giả sử M(x₀;y₀), khi đó: sin⁡α = y₀,cos⁡α = x₀.

Khi x₀≠0, tỉ số y₀/x₀ được gọi là tang của góc α, kí hiệu là tan α.

Khi y₀≠0, tỉ số x₀/y₀ được gọi là côtang của góc α, kí hiệu là cot α.

2. Các hệ thức lượng giác cơ bản

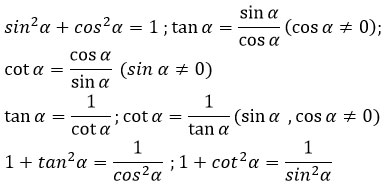
Lý thuyết Hình học 10

Giá trị lượng giác của hai góc phụ nhau

sin⁡(90^o-α) = cos⁡α; cos⁡(90^o-α) = sin⁡α (0^o ≤ α ≤ 90^o)

tan⁡(90^o-α) = cot⁡α; cot⁡(90^o-α) = tan⁡α, (0^o ≤ α ≤ 90^o)

3. Giá trị lượng giác của hai góc bù nhau

sin⁡(180^o-α) = sin⁡α; cos⁡(180^o-α) = -cos⁡α

tan⁡(180^o-α) = -tan⁡α; cot⁡(180^o-α) = -cot⁡α

4. Giá trị lượng giác của các góc đặc biệt

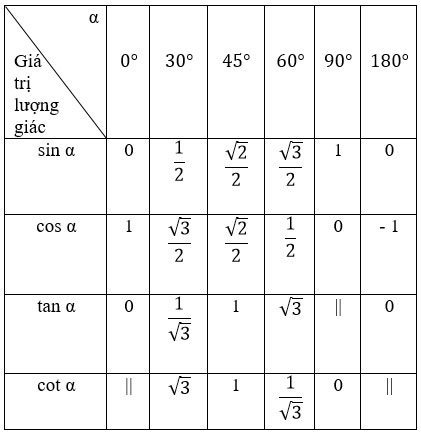
Lý thuyết Hình học 10

5. Góc giữa hai vectơ

Cho hai vectơ $\underset{a}{\rightarrow}$ $\underset{a}{\rightarrow}$ và $\underset{b}{\rightarrow}$ $\underset{b}{\rightarrow}$ khác vectơ – không. Từ một điểm O bất kì ta vẽ $\underset{OA}{\rightarrow}$ $\underset{OA}{\rightarrow}$ = $\underset{a}{\rightarrow}$ $\underset{a}{\rightarrow}$ và $\underset{OB}{\rightarrow}$ $\underset{OB}{\rightarrow}$ = $\underset{b}{\rightarrow}$ $\underset{b}{\rightarrow}$. Khi đó góc AOB với số đo từ 0^o đến 180^o được gọi là góc giữa hai vectơ $\underset{a}{\rightarrow}$ $\underset{a}{\rightarrow}$ và $\underset{b}{\rightarrow}$ $\underset{b}{\rightarrow}$ và kí hiệu là ( $\underset{a}{\rightarrow}$ $\underset{a}{\rightarrow}$, $\underset{b}{\rightarrow}$ $\underset{b}{\rightarrow}$).

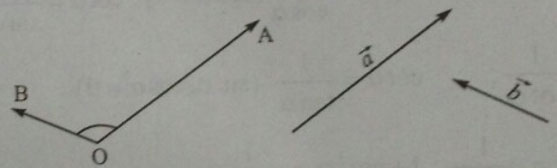
Lý thuyết Hình học 10

Khi ( $\underset{a}{\rightarrow}$ $\underset{a}{\rightarrow}$, $\underset{b}{\rightarrow}$ $\underset{b}{\rightarrow}$) = 90^o, ta nói $\underset{a}{\rightarrow}$ $\underset{a}{\rightarrow}$ ⊥ $\underset{b}{\rightarrow}$ $\underset{b}{\rightarrow}$

Nếu một trong hai vectơ $\underset{a}{\rightarrow}$ $\underset{a}{\rightarrow}$, $\underset{b}{\rightarrow}$ $\underset{b}{\rightarrow}$ bằng $\underset{0}{\rightarrow}$ $\underset{0}{\rightarrow}$ thì ( $\underset{a}{\rightarrow}$ $\underset{a}{\rightarrow}$, $\underset{b}{\rightarrow}$ $\underset{b}{\rightarrow}$) có số đo tùy ý (từ 0^o đến 180^o).

6. Chú ý

Khi giải bài tập trắc nghiệm, học sinh cần chú ý thêm cả kĩ năng loại trừ phương án. Trong nội dung này, học sinh cần ghi nhớ

Góc bất kì từ 0^o đến 180^o có sin thuộc đoạn [0; 1]

Góc bất kì từ 0^o đến 180^o có côsin thuộc đoạn [-1 ; 1]

Góc tù có côsin thuộc ( -1; 0), tang nhỏ hơn 0 và côtang nhỏ hơn 0

Chia sẻ, đánh giá bài viết

1

2.139