Số trung bình cộng - Số trung vị - Mốt
Chuyên đề Toán học lớp 10: Số trung bình cộng - Số trung vị - Mốt được VnDoc sưu tầm và giới thiệu tới các bạn học sinh cùng quý thầy cô tham khảo. Mời các bạn cùng theo dõi bài viết dưới đây nhé.
Bài: Số trung bình cộng - Số trung vị - Mốt
1. Số trung bình cộng
Kí hiệu: 
\(\overline x\)
Bảng phân bố tần suất và tần số:
| Tên dữ liệu | Tần số | Tần suất (%) |
|
x1 x2 . xk |
n1 n2 . nk |
f1 f2 . fk |
| Cộng | n = n1 + … + nk | 100% |
Trung bình cộng của các số liệu thống kê được tính theo công thức:
\(\overline x = \frac{1}{n}\left( {{n_1}{x_1} + {n_2}{x_2} + ... + {n_k}{x_k}} \right) = {f_1}{x_1} + {f_2}{x_2} + ... + {f_k}{x_k}{\text{ }}\left( 1 \right)\)
Trường hợp Bảng phân bố tần suất và tần số ghép lớp
\(\overline x = \frac{1}{n}\left( {{n_1}{c_1} + {n_2}{c_2} + ... + {n_k}{c_k}} \right) = {f_1}{c_1} + {f_2}{c_2} + ... + {f_k}{c_k}{\text{ }}\left( 2 \right)\)
Trong đó: ci, fi, ni là giá trị đại diện của lớp thứ i.
Ý nghĩa của số trung bình:
Trong thực tiễn, để tìm hiểu một đối tượng thống kê ra đưa ra tiêu chí thống kê và tiến hành thu thập nhiều lần số liệu thống kê theo tiêu chí đó, tạo thành mẫu số liệu. Căn cứ vào mẫu số liệu đó, ta rút ra những kết luận có ích về đối tượng thống kê. Để kết luận rút ra phản ánh đúng đắn bản chất của đối tượng, ta cần nhận biết được hình thái và xu thế thay đổi của mẫu số liệu. Với cách nhìn nhận như thế, số trung bình cộng của mẫu số liệu có ý nghĩa sau:
Khi các số liệu trong mẫu ít sai lệch với số trung bình cộng, ta có thể giải quyết được vấn đề trên bằng cách lấy số trung bình cộng làm đại diện cho mẫu số liệu.
Chẳng hạn, để dự báo lượng mưa trong tháng 8 của Hà Nội người ta tiến hành đo lượng mưa của từng ngày trong tháng 8 tại Hà Nội, ta được mẫu số liệu gồm 31 số liệu. Số trung bình cộng của mẫu số liệu đó được xem như lượng mưa trung bình tháng 8 của Hà Nội. Thống kê lượng mưa trung bình tháng 8 của Hà Nội trong nhiều năm liên tiếp sẽ cho ta những dự váo (ngày càng chính xác hơn) lượng mưa trung bình tháng 8 của Hà Nội những năm sắp tới.
Ví dụ 1: Một nhà thực vật học đo chiều dài của 74 chiếc lá cây và thu được số liệu sau (đơn vị mm)
| Lớp | Giá trị đại diện | Tần số |
|
[5,45; 5,85) [5,85; 6,25) [6,25; 6,65) [6,65; 7,05) [7,05; 7,45) [7,45; 7,85) [7,85; 8,25) |
5,65 6,05 6,45 6,85 7,25 7,65 8,05 |
5 9 15 19 16 8 2 |
| N = 74 |
Khi đó chiều dài trung bình của 74 chiếc lá này là :
\(\overline x \approx \frac{{5.5,65 + 9.6,05 + ... + 8.7,65 + 2.8,05}}{{74}} \approx 6,80\left( {mm} \right)\)
Ví dụ 2: Một nhóm 11 học sinh tham gia một kì thi. Số điểm thi của 11 học sinh đó được sắp xếp từ thấp đến cao như sau: (thang điểm 100): 0 ; 0 ; 63 ; 65 ; 69 ; 70 ; 72 ; 78 ; 81 ; 85 ; 89.
Điểm trung bình là:
\(\overline x \approx \frac{{0 + 0 + 63 + ... + 85 + 89}}{{11}} \approx 61,09\)
Quan sát dãy điểm trên, ta thấy hầu hết (9 em) trong nhóm có số điểm vượt điểm trung bình. Như vậy, điểm trung bình này không phản ánh đúng trình độ trung bình của nhóm.
Ví dụ 3: Cho ba nhóm học sinh:
Nhóm 1 gồm 6 học sinh có cân nặng trung bình là 45kg.
Nhóm 2 gồm 11 học sinh có cân nặng trung bình là 50kg.
Nhóm 3 gồm 8 học sinh có cân nặng trung bình là 42kg.
Hãy tính khối lượng trung bình của cả ba nhóm học sinh trên?
Hướng dẫn giải
Tổng khối lượng của mỗi nhóm lần lượt là: \(\left\{ \begin{matrix}
N_{1} = 6.45kg \\
N_{2} = 11.50kg \\
N_{3} = 8.42kg \\
\end{matrix} \right.\)
Khối lượng trung bình của cả ba nhóm là:
\(\overline{x} = \frac{N_{1} + N_{2} +
N_{3}}{6 + 8 + 11}\)
\(\Rightarrow \overline{x} = \frac{6.45 +
11.50 + 8.42}{25} = 46,24kg\)
Vậy khối lượng trung bình của cả ba nhóm học sinh là \(\overline{x} = 46,24kg\) .
2. Số trung vị
Kí hiệu: Me
Khi các số liệu trong mẫu có sự chênh lệnh rất lớn đối với nhau thì số trung bình khó có thể đại diện cho các số liệu trong mẫu. Có một chỉ số khác thích hợp hơn trong trường hợp này. Đó là số trung vị.
Để tìm trung vị của một mẫu số liệu, ta thực hiện như sau:
- Sắp xếp các giá trị trong mẫu số liệu theo thứ tự không giảm ta được:
\({x_1} < {x_2} < ...{x_n}\)
- Trung vị của mẫu, kí hiệu là \(M_e\) là giá trị chính giữa ở dãy \({x_1};{x_2};...;{x_n}\). Cụ thể:
-
- Nếu số giá trị của mẫu số liệu là số lẻ thì giá trị chính giữa của mẫu là trung vị.
Có nghĩa là: \(n = 2k + 1;k \in \mathbb{N}\), thì trung vị của mẫu là: \({M_e} = {x_{k + 1}}\)
-
- Nếu là số chẵn thì trung vị là trung bình cộng của hai giá trị chính giữa của mẫu.
Có nghĩa là: \(n = 2k;k \in \mathbb{N}\), thì trung vị mẫu là \({M_e} = \frac{1}{2}\left( {{x_k} + {x_{k + 1}}} \right)\)
Ý nghĩa: Trung vị được dùng để đo xu thể trung tâm của mẫu số liệu.
+ Trung vị là giá trị nằm ở chính giữa của mẫu số liệu theo nghĩa: luôn có ít nhất 50% số liệu trong mẫu lớn hơn hoặc bằng trung vị và ít nhất 50% số liệu trong mẫu nhỏ hơn hoặc bằng trung vị.
+ Khi trong mẫu suất hiện một số liệu rất lớn hoặc rất nhỏ thì số trung bình sẽ thay đổi đang kể nhưng trung vị thì ít thay đổi.
+ Nếu những số liệu trong mẫu só sự chênh lệch lớn thì ta nên chọn thêm trung vị làm đại diện cho mẫu số liệu đó nhằm điều chỉnh một số hạn chế khi sử dụng số trung bình cộng. Những kết luận về đối tượng thống kê rút ra khi đó sẽ đáng tin cậy hơn.
Nhận xét:
+ Trung vị không nhất thiết là một số trong mẫu số liệu và dễ tính toán
+ Khi các số liệu trong mẫu không có sự chênh lệch lớn thì số trung bình và trung vị xấp xỉ nhau.
Ví dụ 1: Điểm thi toán của 9 học sinh như sau: 1; 1; 3; 6; 7; 8; 8; 9; 10
Ta có Me = 7
Ví dụ 2: Số điểm thi toán của 4 học sinh như sau: 1; 2,5; 8; 9,5
Ta có Me =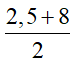 
= 5,25.
Ví dụ: Cho bảng số liệu như sau:
|
Đại diện |
35 |
36 |
37 |
38 |
39 |
40 |
|
Tần số |
7 |
11 |
x |
y |
8 |
5 |
Biết rằng trung vị và cỡ mẫu của mẫu số liệu lần lượt là \(37,5\) và \(50\). Tính giá trị \(x;y\)?
Hướng dẫn giải
Vì cỡ mẫu bằng 50 nên trung vị của mẫu số liệu là trung bình cộng của 2 số ở chính giữa (vị trí 25 và 26).
Mà trung vị của mẫu số liệu trên là \(37,5\)
Hay \(M_{e} = \frac{37 +
38}{2}\)
Từ đó ta có số liệu đứng thứ 25 là 37 và thứ 26 là 38.
Suy ra \(x = 7\)
Mà cỡ mẫu bằng 50 suy ra \(y =
12\)
3. Mốt
Kí hiệu: Mo
Mốt của bảng phân bố tần số là giá trị (xi) có tần số (ni ) lớn nhất và được kí hiệu là Mo.
Chú ý:
Một mẫu số liệu có thể có nhiều mốt.
Khi tất cả các giá trị trong mẫu số liệu có tần số xuất hiện bằng nhau thì mẫu số liệu đó không có mốt.
Có hai giá trị tần số bằng nhau và lớn hơn tần số các giá trị khác thì ta nói trường hợp này có hai Mốt, kí hiệu Mo1,Mo2 .
Ý nghĩa: Mốt của mẫu số liệu đặc trưng cho số lần lặp đi lặp lại nhiều nhất tại một số vị trí của mẫu số liệu đó. Dựa vào mốt, ta có thể đưa ra những kết luận (có ích) về đối tượng thông kê.
Ví dụ: Một cửa hàng bán 6 loại quạt với giá tiền là 100, 150, 300, 350, 400, 500 (nghìn đồng). Số quạt cửa hàng bán ra trong mùa hè vừa qua được thống kê trong bảng tần số sau:
| Giá tiền | 100 | 150 | 300 | 350 | 400 | 500 |
| Số quạt bán được | 256 | 353 | 534 | 300 | 534 | 175 |
Mốt Mo = 300.
Ví dụ: Cho bảng số liệu số máy tính bán được trong quý I đầu năm 2022 của một cửa hàng:
|
Hãng |
HP |
Lenovo |
Asus |
Apple |
Dell |
Razer |
|
Số máy tính bán được |
55 |
45 |
42 |
36 |
60 |
15 |
Mốt của bảng số liệu trên là hãng máy tính nào?
Hướng dẫn giải
Số máy tính bán được nhiều nhất là 60 máy thuộc hãng Dell
=> Mốt của bảng số liệu trên là hãng Dell.
4. Chọn đại diện cho các số liệu thống kê
a) Trường hợp các số liệu thông kê cùng loại và số lượng thống kê đủ lớn (n ≥ 30) thì ta ưu tiên chọn số trung bình làm đại diện cho các số liệu thống kê (về quy mô và độ lớn).
b) Trường hợp không tính được giá trị trung bình thì ta chọn số trung vị hoặc mốt làm đại diện cho các số liệu thống kê (về quy mô và độ lớn).
c) Không nên dùng số trung bình để đại diện cho các số liệu thống kê trong các trường hợp sau (có thể dùng số trung vị hoặc mốt):
+ Số các số liệu thống kê quá ít (n ≤ 10).
+ Giữa các số liệu thống kê có sự chênh lệch quá lớn.
+ Đường gấp khúc tần suất không đối xứng, (và nhiều trường hợp khác).
-------------------------
Trên đây VnDoc đã giới thiệu tới các bạn lý thuyết môn Toán học 10: Số trung bình cộng - Số trung vị - Mốt. VnDoc xin giới thiệu tới các bạn học sinh cùng tham khảo thêm tài liệu Chuyên đề Toán học 10, Giải bài tập Toán lớp 10, Giải VBT Toán lớp 10 mà VnDoc tổng hợp và giới thiệu tới các bạn đọc
