Hệ trục tọa độ

Chuyên đề Toán học lớp 10: Hệ trục tọa độ được VnDoc sưu tầm và giới thiệu tới các bạn học sinh cùng quý thầy cô tham khảo. Nội dung tài liệu sẽ giúp các bạn học sinh học tốt môn Toán học lớp 10 hiệu quả hơn. Mời các bạn tham khảo.

Bài: Hệ trục tọa độ

1. Trục và độ dài đại số trên trục

a) Trục tọa độ (hay gọi tắt là trục) là một đường thẳng trên đó đã xác định một điểm O gọi là điểm gốc và một vectơ đơn vị

Ta kí hiệu trục đó là (O; ).

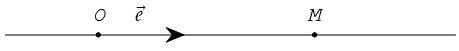
b) Cho M là một điểm tùy ý trên trục (O; ). Khi đó có duy nhất một số k sao cho Ta gọi số k đó là tọa độ của điểm M đối với trục đã cho.

c) Cho hai điểm A và B trên trục (O; ). Khi đó có duy nhất số a sao cho Ta gọi số a là độ dài đại số của vectơ đối với trục đã cho và kí hiệu a =

Nhận xét.

Nếu cùng hướng với thì = AB, còn nếu ngược hướng với thì = –AB.

Nếu hai điểm A và B trên trục (O; ) có tọa độ lần lượt là a và b thì = b – a .

2. Hệ trục tọa độ

a) Định nghĩa: Hệ trục tọa độ (O; ;) gồm hai trục (O;) và (O;) vuông góc với nhau. Điểm gốc O chung của hai trục gọi là gốc tọa độ. Trục (O;) được gọi là trục hoành và kí hiệu là Ox, trục (O; ) được gọi là trục tung và kí hiệu là Oy. Các vectơ và là các vectơ đơn vị trên Ox và Oy và Hệ trục tọa độ (O; ;) còn được kí hiệu là Oxy

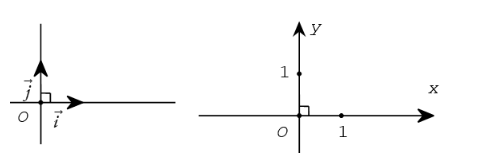
Mặt phẳng mà trên đó đã cho một hệ trục tọa độ Oxy còn được gọi là mặt phẳng tọa độ Oxy hay gọi tắt là mặt phẳng Oxy.

b) Tọa độ của vectơ

Trong mặt phẳng Oxy cho một vectơ và gọi A₁, A₂ lần lượt là hình chiếu của vuông góc của A lên Ox và Oy. Ta có và cặp số duy nhất (x; y) để

Như vậy

Cặp số (x; y) duy nhất đó được gọi là tọa độ của vectơ đối với hệ tọa độ Oxy và viết = (x; y) hoặc (x; y). Số thứ nhất x gọi là hoành độ, số thứ hai y gọi là tung độ của vectơ

Như vậy

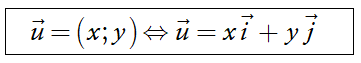
Nhận xét. Từ định nghĩa tọa độ của vectơ, ta thấy hai vectơ bằng nhau khi và chỉ khi chúng có hoành độ bằng nhau và tung độ bằng nhau.

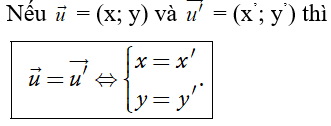
c) Tọa độ của một điểm

Trong mặt phẳng tọa độ Oxy cho một điểm M tùy ý. Tọa độ của vectơ đối với hệ trục Oxy được gọi là tọa độ của điểm M đối với hệ trục đó.

Như vậy, cặp số (x; y) là tọa độ của điểm M khi và chỉ khi Khi đó ta viết M(x; y) hoặc M = (x; y). Số x được gọi là hoành độ, còn số y được gọi là tung độ của điểm M. Hoành độ của điểm M còn được kí hiệu là xM, tung độ của điểm M, còn được kí hiệu là y_M.

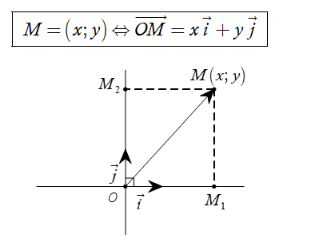
Chú ý rằng, nếu MM₁ ⊥ Ox, MM₂ ⊥ Oy thì

d) Liên hệ giữa tọa độ của điểm và tọa độ của vectơ trong mặt phẳng

Cho hai điểm A(x_A, y_A) và B(x_B, y_B). Ta có

3. Tọa độ của các vectơ

Ta có các công thức sau:

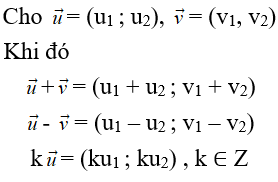
Nhận xét. Hai vectơ cùng phương khi và chỉ khi có một số k sao cho u₁ = kv₁ và u₂ = kv₂.

4. Tọa độ trung điểm của đoạn thẳng. Tọa độ trọng tâm của tam giác

a) Cho đoạn thẳng AB có A(x_A, y_A), B(x_B, y_B). Ta dễ dàng chứng minh được tọa độ trung điểm I(x_I, y_I) của đoạn thẳng AB là

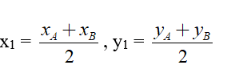
b) Cho tam giác ABC có A(x_A, y_A), B(x_B, y_B), C(x_C, y_C). Khi đó tọa độ của trọng tâm G(x_G, y_G) của tam giác ABC được tính theo công thức

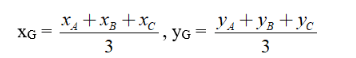
Với nội dung bài Hệ trục tọa độ trên đây chúng tôi xin giới thiệu tới các bạn học sinh cùng quý thầy cô nội dung cần nắm vững khái niệm trục tọa độ, hệ trục tọa độ, tọa độ trung tâm của tam giác...

Trên đây VnDoc đã giới thiệu tới các bạn lý thuyết môn Toán học 10: Hệ trục tọa độ. Để có kết quả cao hơn trong học tập, VnDoc xin giới thiệu tới các bạn học sinh tài liệu Chuyên đề Toán học 10, Giải bài tập Toán lớp 10, Giải VBT Toán lớp 10 mà VnDoc tổng hợp và giới thiệu tới các bạn đọc