Bài tập trắc nghiệm kiểm tra chương 1 Toán 12

Câu hỏi trắc nghiệm chương 1 Toán 12 có đáp án

Trắc nghiệm Toán lớp 12

Mời quý thầy cô cùng các em học sinh tham khảo bài Trắc nghiệm kiểm tra chương 1 Toán 12, với nhiều dạng câu hỏi lý thuyết cũng như bài tập vận dụng bám sát vào nội dung trọng tâm về hàm số, khảo sát hàm số, sự biến thiên của đồ thị hàm số,.... phục vụ quá trình dạy và học tập môn giải tích lớp 12.

Để tiện trao đổi, chia sẻ kinh nghiệm về giảng dạy và học tập các môn học lớp 12, VnDoc mời các thầy cô giáo, các bậc phụ huynh và các bạn học sinh truy cập nhóm riêng dành cho lớp 12 sau: Nhóm Tài liệu học tập lớp 12. Rất mong nhận được sự ủng hộ của các thầy cô và các bạn.

Ôn tập chương 1 Toán đại lớp 12

Câu 1 : Cho hàm số y = x³ – 6x² + 2. Tìm khẳng định sai.

A. Hàm số nghịch biến trên khoảng (0;4)

B. Hàm số đồng biến trên khoảng (4;+ ∞)

C. Điểm cực đại của hàm số là x = 4

D. Điểm cực đại của hàm số là x = 0

Câu 2: Trong các hàm số sau, hàm số nào đồng biến trên R?

A. y = x³+ 3x² + 3x + 1

B. y = x³ + 3x² + 1

C. y = x⁴ + 2x² + 1

D. y =x³ + 2x² – x + 1

Câu 3: Cho hàm số y = f(x) có đồ thị như hình bên. Tìm khẳng định sai

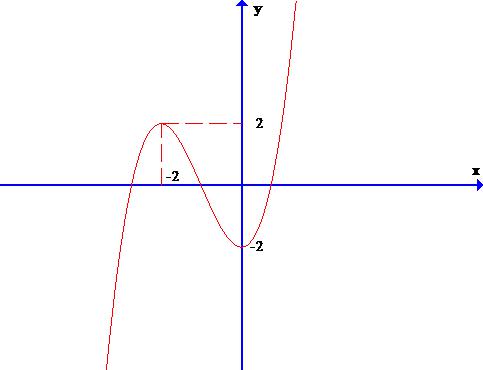
Toán 12 chương 1

A. Hàm số đồng biến trên khoảng (0;+ ∞ )

B. Hàm số nghịch biến trên khoảng (-2;0)

C. Hàm số có điểm cực đại x = 0 và điểm cực tiểu x = - 2

D. Hàm số có điểm cực đại x = -2 và điểm cực tiểu x = 0

Câu 4: Trong các hàm số sau, hàm số nào có 3 cực trị

A. y = x⁴+ x²– 1

B. y = x³ – 3x² – 3x – 1

C. y = - x⁴+ 4x² + 1

D. y = -x⁴ – 4x² + 1

Câu 5: Cho hàm số y = . Tìm khẳng định đúng.

A. Hàm số nghịch biến trên các khoảng xác định

B. Đồ thị hàm số có tiệm cận ngang x = 2

C. Đồ thị hàm số có tiệm cận đứng y = 2

D. Đồ thi không cắt trục hoành

Câu 6: Cho hàm số y = . Gọi S là tập hợp tất cả các giá trị nguyên của m để hàm số đồng biến trên các khoảng xác định. Tìm số phần tử của S.

A. 1

B. 2

C. vô số

D. 3

Câu 7: Gọi A, B là hai điểm cực trị của đồ thị hàm số y = x³ – 6x² +9x -1. Tính độ dài đoạn AB

A. AB = 4

B. AB = 2√5

C. AB = 1

D. AB = √5

Câu 8: Cho hàm số y = f(x) có bảng biến thiên như hình bên. Số điểm cực trị của hàm số là

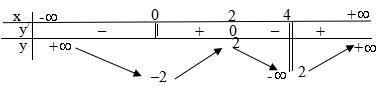
Toán 12 chương 1

A. 2

B. 4

C. 1

D. 0

Câu 9: Trong các hàm số sau, hàm số nào không có cực trị?

A. _{$y = x^2+1$}

B. _{$y = x^3 + 1$}

C. _{$y = x^4 + 1$}

D.

$y = |x|$

Câu 10: Tìm khoảng đồng biến của y = -x⁴ + 2x² + 4.

A. (-∞; -1)

B. (3;4)

C. (0;1)

D. (-∞; -1), (0; 1)

Câu 11: Hàm số nghịch biến trên khoảng:

A. (0;1)

B. (1;+∞)

C.(1;2)

D. (0;2)

Câu 12: Điểm cực đại của đồ thị hàm số y =

A.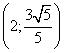

B. (-1 ;0)

C. (0;1)

D. (1; √2)

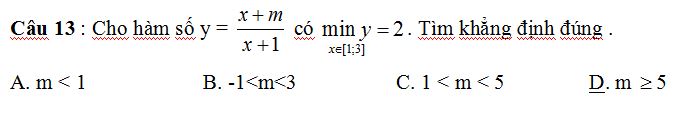
Toán 12 chương 1

Câu 15: Cho bảng biến thiên của hàm số y = f(x). Tìm khẳng định sai.

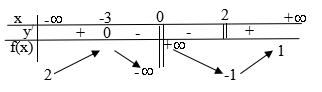
Toán 12 chương 1

A. Đồ thị hàm số có tiệm cận đứng: x = 0 .

B. Đồ thị hàm số có tiệm cận ngang y = 2.

C. Đồ thị hàm số có 4 tiệm cận.

D. Đồ thị hàm số có 3 tiệm cận.

Câu 16: Cho đồ thị hàm số y = x³ – 6x² + 9x – 1 có hai điểm cực trị là A, B. Tìm điểm M trong các điểm sau để A, B, M thẳng hàng.

A. M(4;3)

B. M(4;-3)

C.M(3;4)

D.M(3;-4)

Câu 17: Đồ thị cho bởi hình bên là đồ thị của hàm số nào?

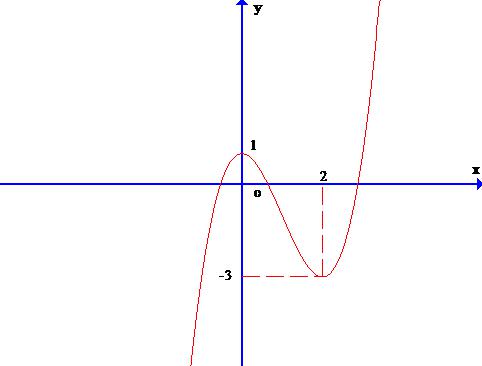
Toán 12 chương 1

A. y = x³– 3x²+ 1

B. y = x³ – 3x² + 2

C. y = – x³+ 3x²+ 1

D. y = x³ + 3x² + 1

Câu 18 :Giá trị nhỏ nhất của hàm số y = x³ – 3x + 2017 trên đoạn [0;2]

A. 2017

B. 2015

C. 2019

D. 2016

Câu 19: Cho hàm số y = f(x) có đồ thị như hình bên. Tìm khẳng định sai.

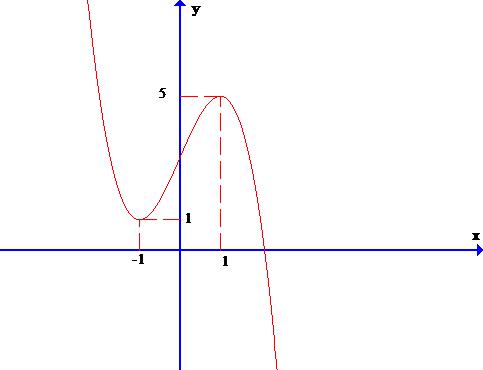
Toán 12 chương 1

A. Hai điểm cực trị của hàm số trái dấu.

B. Hai điểm cục trị của đồ thị hàm số nằm cùng phía đối với trục hoành.

C. Tích hai giá trị cực trị của hàm số là số dương.

D. Khoảng cách giữa hai điểm cực trị là 4.

Câu 20: Gọi A là giao điểm của tiệm cận đứng và tiệm cận ngang của đồ thị hàm số y = , O là gốc tọa độ. Khi đó:

A. OA = 6

B. OA = 4

C. OA = 7

D. OA = 5

Câu 21. Cho hàm số y = x³ – 3x² + mx + 2. Tìm giá trị của m sao cho hàm số đạt cực trị tại x₁, x₂ thỏa mãn x₁² + x₂² = 3.

A. m = 1

B. m = –2

C. m = 3/2

D. m = 1/2

Câu 22. Cho hàm số y = x³ – 3mx + 1 và A(2; 3). Tìm giá trị của m sao cho đồ thị hàm số có hai điểm cực trị B, C thỏa mãn tam giác ABC cân tại A.

A. m = –1/2

B. m = 1/2

C. m = –3/2

D. m = 0

Câu 23. Hàm số nào dưới đây không có cực trị?

A. y = –2x³ + 3x²

B. y = x⁴+ 8x² + 4

C. y = x⁴– 2x² + 1

D. y = x³ – 3x² + 9x

Câu 24. Cho hàm số y = x³ + 3x. Chọn phát biểu đúng.

A. Hàm số đồng biến trên R

B. Hàm số có hai cực trị

C. Hàm số có một tiệm cận

D. Hàm số không có tâm đối xứng

Câu 25. Cho hàm số y = x³ – 3mx² + 3(m² – m)x + 2018. Tìm giá trị của m để hàm số đạt cực trị tại x₁, x₂ thỏa mãn x_1.x₂ = 2.

A. m = 1

B. m = –1

C. m = 0

D. m = 2

Câu 26. Cho hàm số y = –x³ + 3x². Trong số các tiếp tuyến với (C), tiếp tuyến có hệ số góc lớn nhất là

A. y = 3x + 2

B. y = –3x + 15

C.y = 3x – 1

D. y = 9x + 7

Câu 27. Tìm giá trị của m để hàm số y = x³ – 3x² + mx – 2 đạt cực tiểu tại x_o = 2.

A. m = 0

B. m = 1

C. m = –1

D. m = 2

Câu 28. Viết phương trình tiếp tuyến của đồ thị hàm số y = tại điểm có hoành độ bằng 3.

A. y = 4x – 6

B. y = 4x + 6

C. y = –4x + 18

D. y = –4x – 18

Câu 29. Tìm m để hàm số y = x³ – 3(m + 2)x² + 6(m + 6)x – 2 đồng biến trên R.

A. m ≥2 V m ≤ –3

B. –3 ≤ m ≤ 2

C. m ≤ –4 V m ≥ 2

D. –4 ≤ m ≤ 2

Câu 30. Cho hàm số y = x³ – 3x + 2. Gọi A(x₁; y₁) và B(x₂; y₂) là hai điểm cực trị của đồ thị hàm số. Giá trị của y₁ + y₂ là;

A. 0

B. 2

C. –2

D. 4

Câu 31: Trong các khẳng định sau về hàm số: $y=\dfrac{2x-4}{x-1}$ $y=\dfrac{2x-4}{x-1}$, hãy tìm khẳng định đúng?

A. Hàm số có một điểm cực trị

B. Hàm số có một điểm cực đại và một điểm cực tiểu

C. Hàm số đồng biến trên từng khoảng xác định

D. Hàm số nghịch biến trên từng khoảng xác định

Câu 32: Hàm số _{$y=x^3-3x^2+3x-2$}

A. Hàm số nghịch biến trên $\mathbb{R}$ $\mathbb{R}$

B. Hàm số luôn đồng biến trên $\mathbb{R}$ $\mathbb{R}$

C. Hàm số đồng biến trên khoảng $(1,+\infty)$ $(1,+\infty)$

D. Hàm số nghịch biến trên khoảng $(-\infty,-1)$ $(-\infty,-1)$

Câu 33: Cho hàm số $y=x^3-(2m^2-3m+2)x+1$. Kết luận nào sau đây đúng?

A. Hàm số luôn đồng biến trên $\mathbb{R}$ $\mathbb{R}$

B. Hàm số không đơn điệu trên $\mathbb{R}$ $\mathbb{R}$

C. Hàm số luôn nghịch biến trên $\mathbb{R}$ $\mathbb{R}$

D. Hàm số có hai cực trị và khoảng cách giữa hai điểm cực trị bằng 1 với mọi giá trị n.

Câu 34: Tìm m để hàm số $y=f(x)=x^3-6x^2+(m-1)x+2016$ đồng biến trên khoảng $(1,+\infty)$ $(1,+\infty)$

A. $(-13,+\infty)$ $(-13,+\infty)$

B. $(13,+\infty)$ $(13,+\infty)$

C. $\left[-13,+\infty)\right]$ $\left[-13,+\infty)\right]$

D. $[13,+\infty)$ $[13,+\infty)$

--------------------------------------------------------------------

Trên đây VnDoc.com đã giới thiệu tới bạn đọc tài liệu: Bài tập trắc nghiệm kiểm tra chương 1 Toán 12. Chắc hẳn qua bài viết bạn đọc đã nắm được những ý chính cũng như trau dồi được nội dung kiến thức của bài viết rồi đúng không ạ? Bài viết đã tổng hợp các câu hỏi trắc nghiệm kiểm tra chương 1 Toán lớp 12. Hi vọng qua bài viết này bạn đọc có thêm nhiều tài liệu để học tập tốt hơn môn Toán lớp 12 nhé. Để có kết quả cao hơn trong học tập, VnDoc xin giới thiệu tới các bạn học sinh tài liệu Giải bài tập Toán lớp 12, Thi THPT Quốc gia môn Toán, Thi THPT Quốc gia môn Văn, Thi THPT Quốc gia môn Lịch sử mà VnDoc tổng hợp và đăng tải.

Chia sẻ, đánh giá bài viết

11

19.933