Cho hàm số y = f(x) xét sự đơn điệu của hàm g(x) = f(u(x)) + h(x)
Cách xét sự đơn điệu của hàm hợp, hàm ẩn
Trong Giải tích lớp 12, việc xét sự đơn điệu của hàm số là một kỹ năng quan trọng giúp học sinh nắm vững bản chất đạo hàm và phương pháp xác định khoảng đồng biến – nghịch biến. Đối với dạng toán hàm hợp có dạng g(x) = f(u(x)) + h(x), nhiều bạn thường gặp khó khăn trong việc phân tích dấu đạo hàm và xác định mối quan hệ giữa các hàm thành phần.
Bài viết này sẽ hướng dẫn bạn cách xét sự đơn điệu của hàm hợp và hàm ẩn, phân tích chi tiết từng bước, đồng thời đưa ra những mẹo giải nhanh giúp bạn xử lý hiệu quả mọi dạng bài liên quan. Đây là tài liệu hữu ích dành cho học sinh lớp 12, ôn thi THPT Quốc gia và những ai muốn nắm chắc kỹ thuật đạo hàm trong toán học.
A. PHƯƠNG PHÁP GIẢI TOÁN
Bài toán tổng quát: Cho hàm ![]() \(y =
f(x)\) hoặc
\(y =
f(x)\) hoặc  \(y = f'(x)\) xét sự biến thiên của hàm
\(y = f'(x)\) xét sự biến thiên của hàm ![]() \(g(x) = f(u(x)) +
h(x)\).
\(g(x) = f(u(x)) +
h(x)\).
Cách giải:
- Tính  \(g'(x) = u'(x).f'(u(x))
+ h'(x)\)
\(g'(x) = u'(x).f'(u(x))
+ h'(x)\)
- Lập bảng xét dấu  \(g'(x)\) bằng cách cộng dấu của hai biểu thức
\(g'(x)\) bằng cách cộng dấu của hai biểu thức  \(u'(x).f'(u(x))\) và
\(u'(x).f'(u(x))\) và  \(h'(x)\).
\(h'(x)\).
B. BÀI TẬP MINH HỌA XÉT SỰ ĐƠN ĐIỆU CỦA HÀM g(x) = f(u(x)) + h(x)
Ví dụ 1. Cho hàm số ![]() \(f(x)\) có bảng xét dấu của đạo hàm như sau:
\(f(x)\) có bảng xét dấu của đạo hàm như sau:
![]()
Hàm số ![]() \(y = 3f(x + 2) - x^{3} +
3x\) đồng biến trên khoảng nào dưới đây?
\(y = 3f(x + 2) - x^{3} +
3x\) đồng biến trên khoảng nào dưới đây?
A. ![]() \((1; + \infty)\). B.
\((1; + \infty)\). B. ![]() \(( - \infty; - 1)\). C.
\(( - \infty; - 1)\). C. ![]() \(( - 1;0)\). D.
\(( - 1;0)\). D. ![]() \((0;2)\).
\((0;2)\).
Hướng dẫn giải
Ta có  \(y' = 3f'(x + 2) - 3x^{2} +
3 = 3\left\lbrack f'(x + 2) + (1 - x^{2}) \right\rbrack\)
\(y' = 3f'(x + 2) - 3x^{2} +
3 = 3\left\lbrack f'(x + 2) + (1 - x^{2}) \right\rbrack\)
Xét  \(f'(x + 2) = 0 \Leftrightarrow x +
2 \in \{ 1,2,3,4\} \Leftrightarrow x \in \{ - 1,0,1,2\}\)
\(f'(x + 2) = 0 \Leftrightarrow x +
2 \in \{ 1,2,3,4\} \Leftrightarrow x \in \{ - 1,0,1,2\}\)
Xét ![]() \(1 - x^{2} = 0 \Leftrightarrow x = 1,x
= - 1\)
\(1 - x^{2} = 0 \Leftrightarrow x = 1,x
= - 1\)
Lại có:  \(f'(x + 2) > 0
\Leftrightarrow \left\lbrack \begin{matrix}
1 < x + 2 < 3 \\
x + 2 > 4
\end{matrix} \right.\)
\(f'(x + 2) > 0
\Leftrightarrow \left\lbrack \begin{matrix}
1 < x + 2 < 3 \\
x + 2 > 4
\end{matrix} \right.\)
![]() \(\Leftrightarrow \left\lbrack
\begin{matrix}
- 1 < x < 1 \\
x > 2
\end{matrix} \right.\) và
\(\Leftrightarrow \left\lbrack
\begin{matrix}
- 1 < x < 1 \\
x > 2
\end{matrix} \right.\) và ![]() \(1 - x^{2}
> 0 \Leftrightarrow - 1 < x < 1\)
\(1 - x^{2}
> 0 \Leftrightarrow - 1 < x < 1\)
Bảng xét dấu
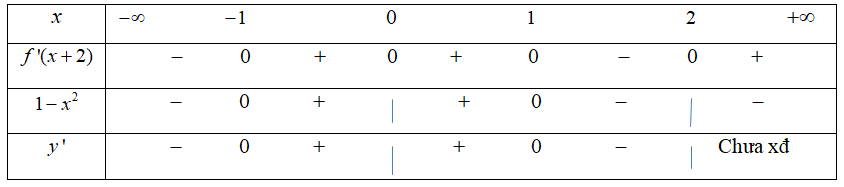
Từ bảng xét dấu suy ra trên khoảng ![]() \(( -
1;0)\) hàm số đồng biến. Chọn đáp án C.
\(( -
1;0)\) hàm số đồng biến. Chọn đáp án C.
Lưu ý:
- Để xác định dấu của  \(y'\) trong bảng trên ta phải cộng dấu của
\(y'\) trong bảng trên ta phải cộng dấu của  \(f'(x + 2)\) và
\(f'(x + 2)\) và ![]() \(\left( 1 - x^{2} \right)\) với nguyên tắc cùng dấu thì cộng được. Nếu khác dấu nhau thì không xác định được dấu của
\(\left( 1 - x^{2} \right)\) với nguyên tắc cùng dấu thì cộng được. Nếu khác dấu nhau thì không xác định được dấu của  \(y'\).
\(y'\).
- Dó đó ta có thể giải  \(f'(x + 2) >
0\) và
\(f'(x + 2) >
0\) và ![]() \(1 - x^{2} > 0\) rồi lấy giao hai tập nghiệm ta được kết quả hàm số chắc chắn đồng biến trên
\(1 - x^{2} > 0\) rồi lấy giao hai tập nghiệm ta được kết quả hàm số chắc chắn đồng biến trên ![]() \(( - 1;1)\). Nên chọn đáp án là tập
\(( - 1;1)\). Nên chọn đáp án là tập ![]() \(( - 1;0) \subset ( - 1;1)\).
\(( - 1;0) \subset ( - 1;1)\).
- Nếu đề bài cho đồ thị hàm  \(y =
f'(x)\), xét sự biến thiên của hàm
\(y =
f'(x)\), xét sự biến thiên của hàm![]() \(g(x) = f(x) - h(x)\) dẫn đến xét dấu của
\(g(x) = f(x) - h(x)\) dẫn đến xét dấu của  \(g'(x) = f'(x) - h'(x)\) dựa vào sự tương giao đồ thị.
\(g'(x) = f'(x) - h'(x)\) dựa vào sự tương giao đồ thị.
Ví dụ 2. Cho hàm số ![]() \(y = f(x)\) có đạo hàm liên tục trên
\(y = f(x)\) có đạo hàm liên tục trên ![]() \(\mathbb{R}.\) Đồ thị hàm số
\(\mathbb{R}.\) Đồ thị hàm số  \(y = f'(x)\) như hình bên dưới.
\(y = f'(x)\) như hình bên dưới.
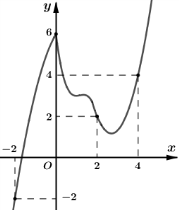
Hàm số ![]() \(g(x) = 2f(x) - x^{2}\) đồng biến trên khoảng nào trong các khoảng sau đây?
\(g(x) = 2f(x) - x^{2}\) đồng biến trên khoảng nào trong các khoảng sau đây?
A. ![]() \(( - \infty; - 2)\). B.
\(( - \infty; - 2)\). B. ![]() \(( - 2;2)\). C.
\(( - 2;2)\). C. ![]() \((2;4)\). D.
\((2;4)\). D. ![]() \((2;
+ \infty)\).
\((2;
+ \infty)\).
Hướng dẫn giải
Ta có  \(g'(x) = 2f'(x) - 2x
\Rightarrow g'(x) = 0 \Leftrightarrow f'(x) = x.\)
\(g'(x) = 2f'(x) - 2x
\Rightarrow g'(x) = 0 \Leftrightarrow f'(x) = x.\)
Số nghiệm của phương trình  \(g'(x) =
0\) chính là số giao điểm của đồ thị hàm số
\(g'(x) =
0\) chính là số giao điểm của đồ thị hàm số  \(y = f'(x)\) và đường thẳng
\(y = f'(x)\) và đường thẳng ![]() \(d:y = x\) (như hình vẽ bên dưới).
\(d:y = x\) (như hình vẽ bên dưới).
Dựa vào đồ thị, suy ra  \(g'(x) = 0
\Leftrightarrow \left\lbrack \begin{matrix}
x = - 2 \\
x = 2 \\
x = 4
\end{matrix} \right.\ .\)
\(g'(x) = 0
\Leftrightarrow \left\lbrack \begin{matrix}
x = - 2 \\
x = 2 \\
x = 4
\end{matrix} \right.\ .\)
Lập bảng biến thiên:
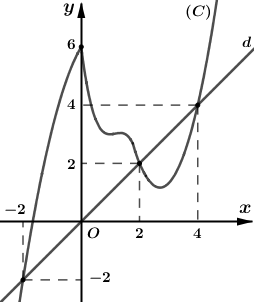
![]() \(\Rightarrow\) hàm số
\(\Rightarrow\) hàm số ![]() \(g(x)\) đồng biến trên
\(g(x)\) đồng biến trên ![]() \(( - 2;2)\) và
\(( - 2;2)\) và ![]() \((4; + \infty)\). So sánh 4 đáp án Chọn B
\((4; + \infty)\). So sánh 4 đáp án Chọn B
Lưu ý: Ta xác định được dấu của  \(g'(x)
= 2\left( f'(x) - x \right)\) theo nguyên tắc: trong khoảng
\(g'(x)
= 2\left( f'(x) - x \right)\) theo nguyên tắc: trong khoảng ![]() \((a;b)\) đồ thị hàm số
\((a;b)\) đồ thị hàm số  \(f'(x)\) nằm phía trên đường thẳng
\(f'(x)\) nằm phía trên đường thẳng ![]() \(y = x\) thì
\(y = x\) thì  \(g'(x) > 0\) .
\(g'(x) > 0\) .
Ví dụ 3. Cho hàm số ![]() \(f(x)\) có bảng xét dấu của đạo hàm như sau:
\(f(x)\) có bảng xét dấu của đạo hàm như sau:
![]()
Hàm số ![]() \(y = 2f(1 - x) + \sqrt{x^{2} + 1} -
x\) nghịch biến trên khoảng nào dưới đây?
\(y = 2f(1 - x) + \sqrt{x^{2} + 1} -
x\) nghịch biến trên khoảng nào dưới đây?
A. ![]() \(( - \infty;1)\). B.
\(( - \infty;1)\). B. ![]() \(( - \infty; - 2)\). C.
\(( - \infty; - 2)\). C. ![]() \(( - 2;0)\). D.
\(( - 2;0)\). D. ![]() \(( - 3; - 2)\).
\(( - 3; - 2)\).
Hướng dẫn giải
Ta có:
![]() \(y' = - 2f'(1 - x) +\frac{x}{\sqrt{x^{2} + 1}} - 1\)
\(y' = - 2f'(1 - x) +\frac{x}{\sqrt{x^{2} + 1}} - 1\) \(= - 2f'(1 - x) + \frac{x -\sqrt{x^{2} + 1}}{\sqrt{x^{2} + 1}}\)
\(= - 2f'(1 - x) + \frac{x -\sqrt{x^{2} + 1}}{\sqrt{x^{2} + 1}}\)
Vì  \(\frac{x - \sqrt{x^{2} +
1}}{\sqrt{x^{2} + 1}} < 0,\forall x\mathbb{\in R}\) nên ta tìm khoảng để:
\(\frac{x - \sqrt{x^{2} +
1}}{\sqrt{x^{2} + 1}} < 0,\forall x\mathbb{\in R}\) nên ta tìm khoảng để:  \(- 2f'(1 - x) \leq 0
\Leftrightarrow f'(1 - x) \geq 0\)
\(- 2f'(1 - x) \leq 0
\Leftrightarrow f'(1 - x) \geq 0\)
![]() \(\Leftrightarrow \left\lbrack
\begin{matrix}
1 \leq 1 - x \leq 3 \\
1 - x \geq 4
\end{matrix} \right.\ \Leftrightarrow \left\lbrack \begin{matrix}
- 2 \leq x \leq 0 \\
x \leq - 3
\end{matrix} \right.\).
\(\Leftrightarrow \left\lbrack
\begin{matrix}
1 \leq 1 - x \leq 3 \\
1 - x \geq 4
\end{matrix} \right.\ \Leftrightarrow \left\lbrack \begin{matrix}
- 2 \leq x \leq 0 \\
x \leq - 3
\end{matrix} \right.\).
So sánh các đáp án, chọn C.
Gợi ý tài liệu tham khảo: Chuyên đề Tương giao đồ thị hàm hợp, hàm ẩn
--------------------------------
Qua nội dung bài viết, bạn đã hiểu rõ cách tìm khoảng đồng biến – nghịch biến cho hàm số dạng g(x) = f(u(x)) + h(x) dựa vào đạo hàm và mối quan hệ giữa hàm hợp và hàm ẩn. Khi nắm được bản chất f'(u(x))·u'(x) + h′(x), bạn có thể tự tin giải quyết nhanh mọi bài toán về đơn điệu xuất hiện trong chương trình Giải tích và đề thi.









