Cách giải nhanh tỉ số thể tích khối chóp tam giác
Tính tỉ số thể tích hình chóp - Có đáp án
Trong phần Hình học không gian của chương trình ôn thi THPT Quốc gia môn Toán, dạng bài tính tỉ số thể tích khối chóp tam giác là dạng toán quen thuộc nhưng dễ gây nhầm lẫn nếu học sinh không nắm được bản chất và phương pháp giải nhanh. Việc hiểu rõ cấu trúc khối chóp, ứng dụng hệ số tỉ lệ và kỹ thuật suy luận hình học giúp rút gọn bài toán đáng kể, từ đó tối ưu thời gian làm bài. Bài viết này sẽ hướng dẫn bạn các cách giải nhanh, mẹo xử lý và phương pháp tổng quát giúp đạt điểm tối đa ở dạng toán này.
A. Công thức tỉ số thể tích khối chóp tam giác
Cho khối chóp tam giác 
\(S.ABC\) . Mặt phẳng \((P)\) cắt các đường thẳng \(SA,SB,SC\) lần lượt tại \(A',B',C'\) . Khi đó ta có:
\(\frac{V_{S.A'B'C'}}{V_{S.ABC}} =
\frac{SA'}{SA}.\frac{SB'}{SB}.\frac{SC'}{SC}\).
B. Bài tập minh họa giải toán tỉ số thể tích khối chóp tam giác
Ví dụ 1. Cho khối chóp \(S.ABC\) có đáy \(ABC\) là tam giác đều cạnh \(a\), \(SA =
2a\) và \(SA\) vuông góc với đáy. Gọi \(M\), \(N\) lần lượt là hình chiếu vuông góc của \(A\) lên các đường thẳng \(SB\) và \(SC\). Tính tỉ số thể tích \(\frac{V_{A.BCNM}}{V_{S.ABC}}\).
Hướng dẫn giải
Hình vẽ minh họa:
Ta có \(\frac{SM}{SB} =
\frac{SM.SB}{SB^{2}} = \frac{SA^{2}}{SB^{2}} = \frac{4}{5}\).
Tương tự \(\frac{SN}{SC} =
\frac{4}{5}\).
\(\frac{V_{S.AMN}}{V_{S.ABC}} =
\frac{SM}{SB}.\frac{SN}{SC} = \left( \frac{4}{5} \right)^{2}\) \(\Rightarrow \frac{V_{A.BCNM}}{V_{S.ABC}} =
\frac{9}{25}\)
Ví dụ 2. Cho tứ diện \(ABCD\) có các cạnh \(AB,\) \(AC\) và \(AD\) đôi một vuông góc. Các điểm \(M,\ \ N,\ \ P\) lần lượt là trung điểm các đoạn thẳng \(BC,\ \ CD,\ BD.\) Biết rằng \(AB = 4a\), \(AC = 6a\), \(AD =
7a\). Tính thể tích \(V\) của khối tứ diện \(AMNP\).
A. \(V = 7a^{3}.\) B. \(V = 28a^{3}.\) C. \(V = 14a^{3}.\) D. \(V = 21a^{3}.\)
Hướng dẫn giải
Hình vẽ minh họa:
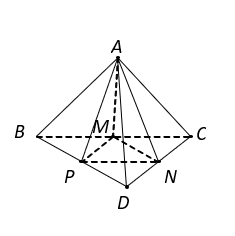
Tứ diện \(ABCD\) có các cạnh \(AB,\) \(AC\) và \(AD\) đôi một vuông góc nên \(V_{ABCD} = \frac{1}{6}AB.AC.AD =
28a^{3}.\)
Ta có\(S_{\Delta MNP} =
\frac{1}{4}S_{\Delta BCD}\), suy ra \(V_{AMNP} = \frac{1}{4}V_{A.BCD} =
7a^{3}.\)
Chọn A.
Ví dụ 3. Cho tứ diện \(ABCD\) có thể tích \(V\). Gọi \(V'\) là thể tích của khối tứ diện có các đỉnh là trọng tâm của các mặt của khối tứ diện \(ABCD.\) Tính tỉ số \(\frac{V'}{V}.\)
A. \(\frac{V'}{V} =
\frac{8}{27}.\) B. \(\frac{V'}{V} =
\frac{23}{27}.\)
C. \(\frac{V'}{V}
= \frac{1}{27}.\) D. \(\frac{V'}{V}
= \frac{4}{27}.\)
Hướng dẫn giải
Hình vẽ minh họa:
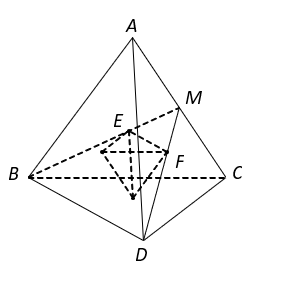
Gọi \(M\) là trung điểm \(AC;\) \(E,\
F\) làn lượt là trọng tâm của tam giác \(ABC,\ ACD.\)
Trong tam giác \(MBD\) có \(EF = \frac{1}{3}BD.\)
Tương tự ta có các cạnh còn lại của tứ diện mới sinh ra bằng \(\frac{1}{3}\) cạnh của tứ diện ban đầu.
Do đó \(\frac{V'}{V} = \left(
\frac{1}{3} \right)^{3} = \frac{1}{27}.\) Chọn C.
C. Bài tập vận dụng tính tỉ số thể tích khối chóp có đáp án chi tiết
Bài tập 1. Cho hình chóp \(S.ABC\) có chiều cao bằng \(9\), diện tích đáy bằng \(5\). Gọi \(M\) là trung điểm của cạnh \(SB\) và \(N\) thuộc cạnh \(SC\) sao cho \(NS
= 2NC.\) Tính thể tích \(V\) của khối chóp \(A.BMNC\).
A. \(V = 15.\) B. \(V = 5.\) C. \(V =
30.\) D. \(V = 10.\)
Bài tập 2. Cho khối chóp \(S.ABC\) có thể tích bằng \(16.\) Gọi \(M,\ N,\ P\) lần lượt là trung điểm các cạnh \(SA,\ SB,\ SC.\) Tính thể tích \(V\) của khối tứ diện \(AMNP.\)
A. \(V = 2.\) B. \(V = 4.\) C. \(V =
6.\) D. \(V = 8.\)
Bài tập 3. Cho tứ diện \(ABCD\) có thể tích \(V\). Xét các điểm \(P\) thuộc đoạn \(AB\), điểm \(Q\) thuộc đoạn \(BC\) và điểm \(R\) thuộc đoạn \(BD\) sao cho \(\frac{PA}{PB} = 2,\ \ \frac{QB}{QC} = 3,\ \
\frac{RB}{RD} = 4\). Tính thể tích của khối tứ diện \(BPQR\) theo \(V.\)
Toàn bộ nội dung đã sẵn sàng! Nhấn Tải về để tải đầy đủ tài liệu.
----------------------------------------
Dạng toán tỉ số thể tích khối chóp tam giác hoàn toàn có thể làm nhanh nếu bạn nắm vững phương pháp và rèn luyện thường xuyên. Hy vọng bài viết đã giúp bạn hiểu sâu cách suy luận, áp dụng được các công thức rút gọn và tăng tốc độ giải khi làm bài thi THPT Quốc gia môn Toán. Hãy tiếp tục luyện tập thêm nhiều bài mẫu để nâng cao độ chính xác và tự tin trong kỳ thi sắp tới.
