Tính nhanh cực trị hàm trị tuyệt đối

Công thức tính nhanh cực trị hàm trị tuyệt đối môn Toán lớp 12 vừa được VnDoc.com biên soạn và xin gửi tới bạn đọc cùng tham khảo. Mời các bạn cùng theo dõi bài viết dưới đây.

A. Cực trị của hàm trị tuyệt đối |f(x)|

Lưu ý:

• Giao điểm không đổi dấu của f(x) với trục Ox là những điểm mà tại đó y = f(x) cắt trục Ox và hàm số y = f(x) không đổi dấu khi đi qua đó.
• Giao điểm đổi dấu của f(x) với trục Ox là những điểm mà tại đó y = f(x) cắt trục Ox và hàm số y = f(x) đổi dấu khi đi qua điểm đó.

Ví dụ. Cho hàm số y = f(x) = ax³ + bx² + cx + d có đồ thị cắt trục \(Ox\) tại ba điểm phân biệt. Hỏi số cực trị của hàm số y = |f(x)| bằng bao nhiêu?

Hướng dẫn giải

Vì đồ thị hàm số y = f(x) = ax³ + bx² + cx + d cắt trục hoành tại ba điểm phân biệt nên hàm số có 2 điểm cực trị giả sử đồ thị của hàm số đó như sau:

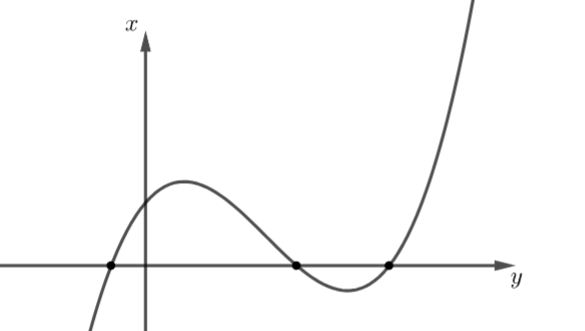
Số điểm cực trị của hàm số là \(2\)

Số nghiệm bội lẻ của phương trình là \(3\)

Khi đó số điểm cực trị của hàm số \(y = \left| f(x) \right|\) là 2 + 3 = 5.

Ví dụ. Cho hàm số y = f(x) có bảng biến thiên như sau:

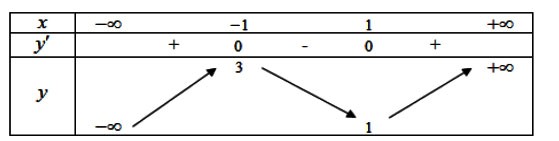
Tìm số điểm cực trị của hàm số \(g(x) = \left| f(x) - 2 \right|\) ?

Hướng dẫn giải

Số điểm cực trị của hàm số \(g(x) = \left| f(x) - 2 \right| = m + n\)

Với m là số điểm cực trị của hàm số \(y = f(x) - 2 \Rightarrow m = 2\)

n là số nghiệm bội lẻ của phương trình \(f(x) = 2 \Rightarrow n = 3\)

Suy ra số điểm cực trị của hàm số \(g(x) = \left| f(x) - 2 \right| = 2 + 3 = 5\)

B. Cực trị của hàm trị tuyệt đối f(|x|)

Lưu ý: Nếu y = f(x) là hàm hằng trong một khoảng [0; a) (a > 0 tùy ý thuộc tập số thực); hoặc f(x) không xác định tại x = 0 thì công thức trên ta không cộng với 1.

Ví dụ. Cho hàm số y = f(x) có đạo hàm \(f'(x) = (x + 1)\left( x^{2} - 1 \right)(x - 3)^{3};\forall x\mathbb{\in R}\). Hỏi hàm số y = f(|x|) có bao nhiêu cực trị?

Hướng dẫn giải

Ta có:

\(f'(x) = 0 \Leftrightarrow \left\lbrack \begin{matrix} x = - 1 \\ x = 1 \\ x = 3 \\ \end{matrix} \right.\)

Ta có bảng biến thiên như sau:

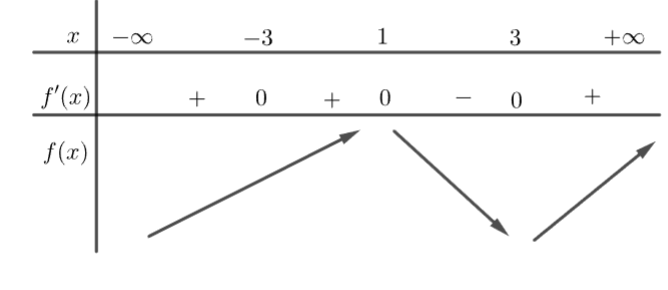
Từ bảng biến thiên ta thấy số điểm cực trị dương của hàm số y = f(x) là 2 nên số điểm cực trị của hàm số \(y = f\left( |x| \right)\) là 5 điểm.

Ví dụ. Cho hàm số y = f(x) có đồ thị như hình vẽ:

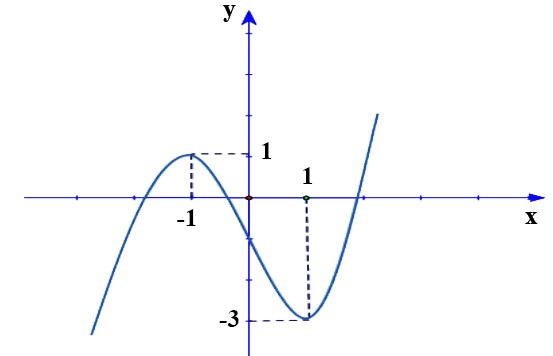
Xác định số điểm cực trị của hàm số \(y = f\left( |x + 2| \right)\)?

Hướng dẫn giải

Tịnh tiến hàm số y = f(x) sang trái hai đơn vị ta được hàm số \(y = f(x + 2)\)

Đồ thị hàm số \(y = f\left( |x + 2| \right)\) có được gồm hai phần.

Phần 1 là phần đồ thị \(y = f(x + 2)\) nằm phía bên phải \(Oy\).

Phần 2 là phần đồ thị đối xứng qua \(Oy\).

Khi đó đồ thị hàm số sẽ có một điểm cực trị.

C. Cực trị của hàm số k₁f(ax + b)+k₂

Số điểm cực trị của hàm số f(x) = Số điểm cực trị của hàm số k₁f(ax + b)+k₂.

---------------------------------------

FAQ

1. Cực trị của hàm trị tuyệt đối là gì?

Cực trị của hàm trị tuyệt đối là các điểm mà tại đó hàm số đạt giá trị cực đại hoặc cực tiểu cục bộ, thường xuất hiện tại các điểm đặc biệt như nghiệm của biểu thức bên trong dấu giá trị tuyệt đối hoặc các điểm tới hạn của hàm số.

2. Vì sao bài toán cực trị hàm trị tuyệt đối thường khó?

Do hàm số chứa dấu giá trị tuyệt đối có thể thay đổi biểu thức trên từng khoảng khác nhau, học sinh cần xét điều kiện để phá dấu giá trị tuyệt đối trước khi khảo sát và tìm cực trị.

3. Có những phương pháp nào để tìm cực trị hàm trị tuyệt đối?

Các phương pháp phổ biến gồm:

• Xét từng khoảng để bỏ dấu giá trị tuyệt đối.
• Sử dụng bảng biến thiên.
• Kết hợp đạo hàm.
• Phân tích đồ thị hàm số.
• Khai thác tính chất đối xứng và biến đổi tương đương.

4. Khi nào cần phá dấu giá trị tuyệt đối?

Cần phá dấu giá trị tuyệt đối khi muốn đưa hàm số về dạng quen thuộc để tính đạo hàm, khảo sát sự biến thiên hoặc xác định các điểm cực trị chính xác.

5. Có thể tìm cực trị hàm trị tuyệt đối mà không cần đạo hàm không?

Có. Một số bài toán có thể giải nhanh bằng cách phân tích đồ thị, xét tính chất của giá trị tuyệt đối hoặc sử dụng bảng biến thiên của hàm số gốc.

---------------------------------

Tính nhanh cực trị hàm trị tuyệt đối là một kỹ năng quan trọng giúp học sinh lớp 12 giải quyết hiệu quả các bài toán khảo sát hàm số và ứng dụng đạo hàm trong đề thi THPT Quốc gia. Việc nắm vững các phương pháp tìm cực trị, kỹ thuật xử lý dấu giá trị tuyệt đối và các mẹo giải nhanh sẽ giúp rút ngắn thời gian làm bài, đồng thời nâng cao độ chính xác khi làm trắc nghiệm. Hy vọng chuyên đề này sẽ là tài liệu hữu ích giúp các em củng cố kiến thức, luyện tập thành thạo dạng toán cực trị hàm trị tuyệt đối và tự tin chinh phục mục tiêu điểm cao môn Toán 12.