Cách bấm máy tính tìm nguyên hàm F(x) của hàm số f(x)
Cách bấm máy tính tìm nguyên hàm
Bạn đang học giải tích và loay hoay không biết cách sử dụng máy tính cầm tay để tìm nguyên hàm một cách nhanh chóng, chính xác? Trong bài viết này, chúng tôi sẽ hướng dẫn cách bấm máy tính tìm nguyên hàm F(x) của hàm số f(x) bằng các dòng máy phổ biến như Casio fx-580VN X hoặc fx-570VN Plus. Đây là một kỹ năng cực kỳ hữu ích giúp bạn kiểm tra kết quả trong quá trình học và luyện thi môn Toán. Hãy cùng khám phá cách làm nhanh chóng chỉ trong vài bước đơn giản!
A. Thuật toán trên máy tính CASIO
\(f(A) -
\frac{d}{dx}(F_{i}(x))\left| \ _{x = A} \right.\)
\(f\): là hàm số cần xác định nguyên hàm
\(F_{i}(x)\): là các đáp án nguyên hàm đã cho
A: hằng số tự chọn thuộc tập xác định và có giá trị nhỏ
- Thay lần lượt các đáp án vào \(F_{i}(x)\) và chọn giá trị A thích hợp
- Lựa chọn đáp án có kết quả xấp xỉ bằng 0
B. Bài tập tìm nguyên hàm nhanh bằng máy tính
Bài toán 1.1 Tìm nguyên hàm của hàm số \(f(x) = \frac{7x^{4} + 3x^{2} + 4x}{2\sqrt{x^{3} +
1}}\)
- \(\int_{}^{}{f(x)dx = (x^{2} +
2x)\sqrt{x^{3} + 1} + C}\)
- \(\int_{}^{}{f(x)dx = (x^{3} +
x)\sqrt{x^{2} + 1} + C}\)
- \(\int_{}^{}{f(x)dx = (x^{2} +
1)\sqrt{x^{3} + 1} + C}\)
- \(\int_{}^{}{f(x)dx = (x^{3} +
x)\sqrt{x^{3} + 1} + C}\)
Phân tích: Hàm số \(f(x)\) trên khá phức tạp do đó việc sử dụng máy tính CASIO fx-580VN X để tìm nguyên hàm sẽ giúp các bạn chọn được đáp án đúng một cách nhanh chóng và chính xác hơn.
Hướng dẫn giải
Thay \(F_{i}(x)\) lần lượt bằng các đáp án và chọn A = 0
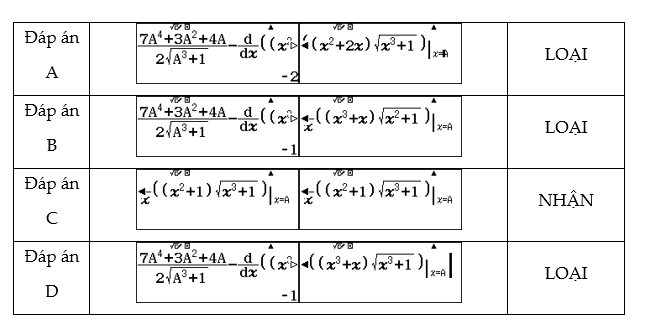
Khi làm bài thi các bạn không cần thử tất cả các đáp án trong đề mà chúng ta sẽ dừng ngay việc thay đáp án khi chọn được biểu thức đúng
Bài toán 1.2 Tìm nguyên hàm của hàm số \(y
= 8sin3xcos2xsin6x\)
- \(\int_{}^{}{f(x)dx = 2sinx +
\frac{2sin5x}{5} - \frac{2sin7x}{7} - \frac{2sin11x}{11} +
C}\)
- \(\int_{}^{}{f(x)dx = \sin x +
\frac{sin5x}{5} + \frac{sin7x}{7} - \frac{sin11x}{11} + C}\)
- \(\int_{}^{}{f(x)dx = \sin x -
\frac{sin5x}{5} - \frac{sin7x}{7} - \frac{sin11x}{11} + C}\)
- \(\int_{}^{}{f(x)dx = 2sinx -
\frac{2sin5x}{5} - \frac{2sin7x}{7} - \frac{2sin11x}{11} +
C}\)
Hướng dẫn giải
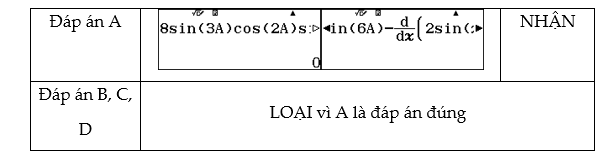
Để các phép toán lượng giác thực hiện chính xác hơn, chúng ta nên chuyển máy về chế độ Radian
Chọn \(A = \pi\)
Bài toán 1.3: Cho hàm số \(F(x) = \frac{1}{2x^{2}}\) là một nguyên hàm của hàm số \(\frac{f(x)}{x}\). Tìm nguyên hàm của hàm số \(f^{/}(x)lnx\)
- \(\int_{}^{}{f^{/}(x)lnxdx = - \left(
\frac{\ln x}{x^{2}} + \frac{1}{x^{2}} \right) + C}\)
- \(\int_{}^{}{f^{/}(x)lnxdx = - \left(
\frac{\ln x}{x^{2}} + \frac{1}{2x^{2}} \right) + C}\)
- \(\int_{}^{}{f^{/}(x)lnxdx = \frac{\ln
x}{x^{2}} + \frac{1}{2x^{2}} + C}\)
- \(\int_{}^{}{f^{/}(x)lnxdx = \frac{\ln
x}{x^{2}} + \frac{1}{x^{2}} + C}\)
Hướng dẫn giải
Ta có \(f(x) = F^{/}(x)x = -
\frac{1}{x^{2}}\), suy ra \(f^{/}(x)lnx
= \frac{2lnx}{x^{3}}\)
Nhập vào máy tính CASIO fx- 580VN X: \(\frac{2lnA}{A^{3}} - \frac{d}{dx}G(x)\left| \ _{x
= A} \right.\) , với G(x) lần lượt là các hàm trong đáp án và A = 0.1
--------------------------------------
Hy vọng hướng dẫn cách bấm máy tính tìm nguyên hàm F(x) trong bài viết đã giúp bạn hiểu rõ và áp dụng hiệu quả vào việc học Toán. Việc sử dụng máy tính đúng cách không chỉ giúp tiết kiệm thời gian mà còn nâng cao độ chính xác trong quá trình làm bài. Đừng quên luyện tập thường xuyên và kết hợp với phương pháp tự luận để đạt kết quả tốt nhất trong kỳ thi!
