VnDoc.com

Tích phân là gì? Khái niệm và các tính chất tích phân dễ hiểu nhất

Khái niệm tích phân và các tính chất cơ bản cần nhớ

Bài trước

Tải về

Bài sau

Tích phân toàn diện: Định nghĩa, tính chất và mẹo ghi nhớ nhanh

A. Tích phân là gì?
B. Hai phương pháp cơ bản để tìm tích phân
- 1. Phương pháp đổi biến số
- 2. Phương pháp tích phân từng phần

Tích phân là một khái niệm quan trọng trong giải tích, giúp tính diện tích, thể tích và các đại lượng liên quan đến sự biến thiên. Bài viết này sẽ giúp bạn hiểu rõ tích phân là gì, đồng thời trình bày các tính chất cơ bản của tích phân một cách ngắn gọn, dễ nhớ và dễ áp dụng. Phù hợp cho học sinh, sinh viên và người mới bắt đầu học giải tích.

A. Tích phân là gì?

1. Định nghĩa tích phân

Cho hàm số $f (x)$ là hàm số liên tục trên đoạn $\lbrack a;b\rbrack$ $[a; b]$ . Giả sử $F (x)$ là một nguyên hàm của $f (x)$ trên đoạn $\lbrack a;b\rbrack$ $[a; b]$ .Hiệu số $F (b) - F (a)$ được gọi là tích phân từ a đến b (hay tích phân xác định trên đoạn $\lbrack a;b\rbrack$ $[a; b]$ ) của hàm số $f (x)$ , kí hiệu là $\int_{a}^{b}{f(x)dx}$ $\int_{a}^{b} f (x) d x$ .Vậy $\int_{a}^{b}{f(x)dx} = \left. \ F(x) \right|_{a}^{b} = F(b) - F(a)$ $\int_{a}^{b} f (x) d x = {F (x) |}_{a}^{b} = F (b) - F (a)$ .

Ta gọi $\int_{a}^{b}‍$ $\int_{a}^{b} ‍$ là dấu tích phân, a là cận dưới, b là cận trên, $f (x) d x$ là biểu thức dưới dấu tích phân và $f (x)$ là hàm số dưới dấu tích phân.

Chú ý:

Định nghĩa tích phân $\int_{a}^{b}{f(x)dx} = F(b) - F(a) = \left. \ F(x) \right|_{a}^{b}$ $\int_{a}^{b} f (x) d x = F (b) - F (a) = {F (x) |}_{a}^{b}$ chỉ được áp dụng khi biết một nguyên hàm $F (x)$ của $f (x)$ trên đoạn $\lbrack a;b\rbrack$ $[a; b]$ .
Tích phân $\int_{a}^{b}{f(x)dx}$ $\int_{a}^{b} f (x) d x$ là một số, còn nguyên hàm là một (họ) hàm số (nó còn được gọi là tích phân không xác định).
$\int_{a}^{b}{f(x)dx}$ $\int_{a}^{b} f (x) d x$ không phụ thuộc vào chữ viết biến số trong dấu tích phân, mà chỉ phụ thuộc vào hàm số f và đoạn $\lbrack a;b\rbrack$ $[a; b]$ .

Nhận xét

Tích phân của hàm số f từ a đến b có thể kí hiệu bởi $\int_{a}^{b}{f(x)dx}$ $\int_{a}^{b} f (x) d x$ hay $\int_{a}^{b}{f(t)dt}$ $\int_{a}^{b} f (t) d t$ .
Tích phân đó chỉ phụ thuộc vào f và các cận a, b mà không phụ thuộc vào biến số x hay t.

2. Ý nghĩa hình học của tích phân

Nếu hàm số $f (x)$ liên tục và không âm trên đoạn $\lbrack a;b\rbrack$ $[a; b]$ , thì tích phân $\int_{a}^{b}{f(x)dx}$ $\int_{a}^{b} f (x) d x$ là diện tích S của hình thang cong giới hạn bởi đồ thị $f (x)$ , trục Ox và hai đường thẳng $x = a; x = b$ . Vậy $S = \int_{a}^{b}{f(x)dx}$ $S = \int_{a}^{b} f (x) d x$ .

3. Các tính chất của tích phân

Tính chất 1

$\int_{a}^{b}{kf(x)dx} = k\int_{a}^{b}{f(x)dx}$ $\int_{a}^{b} k f (x) d x = k \int_{a}^{b} f (x) d x$ với k là hằng số.

Tính chất 2

$\int_{a}^{b}{\left\lbrack f(x) \pm g(x) \right\rbrack dx} = \int_{a}^{b}{f(x)}dx \pm \int_{a}^{b}{g(x)}dx$ $\int_{a}^{b} [f (x) \pm g (x)] d x = \int_{a}^{b} f (x) d x \pm \int_{a}^{b} g (x) d x$

Tính chất 3

$\int_{a}^{c}{f(x)dx} + \int_{c}^{b}{f(x)dx} = \int_{a}^{b}{f(x)dx}$ $\int_{a}^{c} f (x) d x + \int_{c}^{b} f (x) d x = \int_{a}^{b} f (x) d x$ với $a < c < b$ .

Ta quy ước:

$\int_{a}^{b}{f(x)dx} = 0$ $\int_{a}^{b} f (x) d x = 0$ ;
$\int_{a}^{b}{f(x)dx} = - \int_{a}^{b}{f(x)dx}$ $\int_{a}^{b} f (x) d x = - \int_{a}^{b} f (x) d x$

Định lý 1

Cho f là hàm số xác định trên K và a là một điểm cố định thuộc K. Xét hàm số $G (x)$ xác định trên K bởi công thức

$G(x) = \int_{a}^{x}{f(t)dt}$ $G (x) = \int_{a}^{x} f (t) d t$

Khi đó G là một nguyên hàm của f.

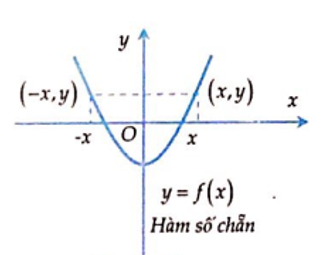
Tích phân hàm chẵn lẻ

Định lý 2: Tích phân của hàm lẻ và hàm chẵn trên $\mathbb{R}$ $R$ .

1. Nếu f là một hàm số chẵn, khi đó $\int_{- a}^{a}{f(x)dx} = 2\int_{0}^{a}{f(x)dx}$ $\int_{- a}^{a} f (x) d x = 2 \int_{0}^{a} f (x) d x$

2. Nếu f là một hàm số lẻ, khi đó $\int_{- a}^{a}{f(x)dx} = 0$ $\int_{- a}^{a} f (x) d x = 0$ .

Đọc thêm

Ta vừa đưa ra 3 tính chất của tích phân theo chương trình chuẩn. Dưới đây là các tính chất bổ sung:

1. $\int_{a}^{b}{0dx} = 0$ $\int_{a}^{b} 0 d x = 0$

2. $\int_{a}^{b}{cdx} = c(b - a)$ $\int_{a}^{b} c d x = c (b - a)$

3. Nếu $f(x) \geq 0,\forall x \in \lbrack a,b\rbrack$ $f (x) \geq 0, \forall x \in [a, b]$ thì $\int_{a}^{b}{f(x)dx} \geq 0$ $\int_{a}^{b} f (x) d x \geq 0$ .

Hệ quả 3: Nếu hai hàm số $f (x)$ và $g (x)$ liên tục và thỏa mãn $f(x) \leq g(x),\forall x \in \lbrack a;b\rbrack$ $f (x) \leq g (x), \forall x \in [a; b]$ thì $\int_{a}^{b}{f(x)dx} \leq \int_{a}^{b}{g(x)dx}$ $\int_{a}^{b} f (x) d x \leq \int_{a}^{b} g (x) d x$

Chú ý: Nếu $f (x)$ liên tục và dương trên $\lbrack a;b\rbrack$ $[a; b]$ thì $\int_{a}^{b}{f(x)dx} > 0$ $\int_{a}^{b} f (x) d x > 0$ .

4. $\left| \int_{a}^{b}{f(x)dx} \right| \leq \int_{a}^{b}{\left| f(x) \right|dx},(a \leq b)$ $| \int_{a}^{b} f (x) d x | \leq \int_{a}^{b} | f (x) | d x, (a \leq b)$ .

5. Nếu $m \leq f(x) \leq M,\forall x \in \lbrack a;b\rbrack;m,M$ $m \leq f (x) \leq M, \forall x \in [a; b]; m, M$ là các hằng số thì $m(b - a) \leq \int_{a}^{b}{f(x)dx} \leq M(b - a)$ $m (b - a) \leq \int_{a}^{b} f (x) d x \leq M (b - a)$ hay $m \leq \frac{1}{b - a}\int_{a}^{b}{f(x)dx} \leq M$ $m \leq \frac{1}{b - a} \int_{a}^{b} f (x) d x \leq M$ .

B. Hai phương pháp cơ bản để tìm tích phân

1. Phương pháp đổi biến số

Định lý 1

Cho hàm số $f (x)$ liên tục trên đoạn $\lbrack a;b\rbrack$ $[a; b]$ . Giả sử hàm số $x = \varphi(t)$ $x = φ (t)$ có đạo hàm liên tục trên đoạn $\lbrack\alpha;\beta\rbrack$ $[α; β]$ sao cho $\varphi(\alpha) = a;\varphi(b) = b$ $φ (α) = a; φ (b) = b$ và $a \leq \varphi(t) \leq b$ $a \leq φ (t) \leq b$ với mọi $t \in \lbrack\alpha;\beta\rbrack$ $t \in [α; β]$ .

Khi đó:

$\int_{a}^{b}{f(x)dx} = \int_{\alpha}^{\beta}{f\left( \varphi(t) \right)\varphi$ $\int_{a}^{b} f (x) d x = \int_{α}^{β} f (φ (t)) φ^{'} (t) d t$

Từ định lý 1 ta rút ra các bước đổi biến số

1. Đặt $x = \varphi(t)$ $x = φ (t)$ , ta xác định đoạn $\lbrack\alpha;\beta\rbrack$ $[α; β]$ sao cho $\varphi(\alpha) = a,\varphi(\beta) = b$ $φ (α) = a, φ (β) = b$ và $a \leq \varphi(t) \leq b$ $a \leq φ (t) \leq b$ , $\forall t \in \lbrack\alpha;\beta\rbrack$ $\forall t \in [α; β]$ ;

2. Biến đổi $f(x)dx = f\left( \varphi(t) \right)\varphi$ $f (x) d x = f (φ (t)) φ^{'} (t) d t = g (t) d t$

3. Tìm một nguyên hàm $G (t)$ của $g (t)$

4. Tính $\int_{\alpha}^{\beta}{g(t)dt} = G(\beta) - G(\alpha)$ $\int_{α}^{β} g (t) d t = G (β) - G (α)$

5. Kết luận $\int_{a}^{b}{f(x)dx} = G(\beta) - G(\alpha)$ $\int_{a}^{b} f (x) d x = G (β) - G (α)$ .

Ví dụ 1: Tính tích phân $I = \int_{0}^{3}{\frac{x^{2}}{(1 + x)^{3}}dx}$ $I = \int_{0}^{3} \frac{x^{2}}{(1 + x)^{3}} d x$ ?

A. $I = ln4 + \frac{33}{32}$ $I = l n 4 + \frac{33}{32}$	B. $I = ln4 - \frac{4121}{4000}$ $I = l n 4 - \frac{4121}{4000}$
C. $I = l n 4 - 1$	D. $I = ln4 - \frac{33}{32}$ $I = l n 4 - \frac{33}{32}$

Đáp án D.

Lời giải

Đặt $1 + x = u \Rightarrow dx = du$ $1 + x = u \Rightarrow d x = d u$ .

Đổi cận $x = 0 \Rightarrow u = 1;x = 3 \Rightarrow u = 4$ $x = 0 \Rightarrow u = 1; x = 3 \Rightarrow u = 4$

Khi đó $I = \int_{1}^{4}{\frac{(u - 1)^{2}}{u^{3}}du} = \int_{1}^{4}\begin{matrix} \frac{u^{2} - 2u + 1}{u^{2}}du \\ \end{matrix}$ $I = \int_{1}^{4} \frac{(u - 1)^{2}}{u^{3}} d u = \int_{1}^{4} \begin{matrix} \frac{u^{2} - 2 u + 1}{u^{2}} d u \end{matrix}$

$= \int_{1}^{4}\left( \frac{1}{u} - \frac{2}{u^{2}} + \frac{1}{u^{3}} \right)du = \left. \ \left( \ln|u| + \frac{2}{u} - \frac{1}{2u^{2}} \right) \right|_{1}^{4}$ $= \int_{1}^{4} (\frac{1}{u} - \frac{2}{u^{2}} + \frac{1}{u^{3}}) d u = {(\ln | u | + \frac{2}{u} - \frac{1}{2 u^{2}}) |}_{1}^{4}$

$= ln4 - \frac{33}{32}$ $= l n 4 - \frac{33}{32}$

Định lý 2

Cho hàm số $f (x)$ liên tục trên đoạn $\lbrack a;b\rbrack$ $[a; b]$ . Nếu hàm số $u = u (x)$ có đạo hàm liên tục trên đoạn $\lbrack a;b\rbrack$ $[a; b]$ và $\alpha \leq u(x) \leq \beta$ $α \leq u (x) \leq β$ với mọi $x \in \lbrack a;b\rbrack$ $x \in [a; b]$ sao cho $f(x) = g\left( u(x) \right)u$ $f (x) = g (u (x)) u^{'} (x), g (u)$ liên tục trên đoạn $\lbrack\alpha;\beta\rbrack$ $[α; β]$ thì

$\int_{a}^{b}{f(x)dx} = \int_{u(a)}^{u(b)}{g(u)du}$ $\int_{a}^{b} f (x) d x = \int_{u (a)}^{u (b)} g (u) d u$

Từ định lý 2 ta rút ra các bước đổi biến số

1. Đặt $u = u (x)$ ,

2. Biến đổi $f (x) d x = g (u) d u$ .

3. Tìm một nguyên hàm $G (u)$ của $g (u)$ .

4. Tính $\int_{u(a)}^{u(b)}{g(u)du} = G\left( u(b) \right) - G\left( u(a) \right)$ $\int_{u (a)}^{u (b)} g (u) d u = G (u (b)) - G (u (a))$ .

5. Kết luận $\int_{a}^{b}{f(x)dx} = G\left( u(b) \right) - G\left( u(a) \right)$ $\int_{a}^{b} f (x) d x = G (u (b)) - G (u (a))$

Ví dụ 2: Tính tích phân $I = \int_{0}^{\frac{\pi}{2}}{sin^{2}x.cosxdx}$ $I = \int_{0}^{\frac{π}{2}} s i n^{2} x . c o s x d x$ ?

A. $I = \frac{1}{2}$

I = \frac{1}{2}

B. $I = \frac{1}{3}$

I = \frac{1}{3}

C. $I = \frac{2}{3}$

I = \frac{2}{3}

D. $I = \frac{1}{5}$

I = \frac{1}{5}

Đáp án B.

Lời giải

Đặt $u = \sin x$ $u = \sin x$ , ta có

$sin^{2}x\cos xdx = sin^{2}x\left( \sin x \right)$ $s i n^{2} x \cos x d x = s i n^{2} x {(\sin x)}^{'} d x = u^{2} d u$ .

Hàm số $g(u) = u^{2};u \in \lbrack 0;1\rbrack$ $g (u) = u^{2}; u \in [0; 1]$ do $\left( u(0) = 0;u\left( \frac{\pi}{2} \right) = 1 \right)$ $(u (0) = 0; u (\frac{π}{2}) = 1)$ có nguyên hàm $G(u) = \frac{u^{3}}{3}$ $G (u) = \frac{u^{3}}{3}$ .

Vậy $\int_{0}^{\frac{\pi}{2}}{sin^{2}x\cos xdx} = \int_{0}^{1}{u^{2}du} = \left. \ \frac{u^{3}}{3} \right|_{0}^{1} = \frac{1}{3}$ $\int_{0}^{\frac{π}{2}} s i n^{2} x \cos x d x = \int_{0}^{1} u^{2} d u = {\frac{u^{3}}{3} |}_{0}^{1} = \frac{1}{3}$ .

2. Phương pháp tích phân từng phần

Tương tự tính nguyên hàm từng phần, ta có định lý sau:

Nếu $u = u (x)$ và $v = v (x)$ là hai hàm số có đạo hàm liên tục trên đoạn $\lbrack a;b\rbrack$ $[a; b]$ thì

$\int_{a}^{b}{u(x)v$ $\int_{a}^{b} u (x) v^{'} (x) d x = {(u (x) v (x)) |}_{a}^{b} - \int_{a}^{b} u^{'} (x) v (x) d x$ hay $\int_{a}^{b}{udv} = \left. \ uv \right|_{a}^{b} - \int_{a}^{b}{vdu}$ $\int_{a}^{b} u d v = {u v |}_{a}^{b} - \int_{a}^{b} v d u$

Chú ý: Trong thực tế, đôi khi việc sử dụng phương pháp tính tích phân từng phần phải linh hoạt, đôi khi phải dự đoán khác thường như ví dụ 1 dưới đây.

Ta có bảng sau

	$\int_{}^{}{P(x)e^{x}dx}$ $\int_{}^{} P (x) e^{x} d x$	$\int_{}^{}{P(x)\cos xdx}$ $\int_{}^{} P (x) \cos x d x$	$\int_{}^{}{P(x)\ln xdx}$ $\int_{}^{} P (x) \ln x d x$
$u$	$P (x)$	$P (x)$	$\ln x$ $\ln x$
$d v$	$e^{x}dx$ $e^{x} d x$	$\cos xdx$ $\cos x d x$	$P (x) d x$

Ví dụ 3: Cho $I = \int_{1}^{2}{\left( 1 + x + \frac{1}{x} \right)e^{x - \frac{1}{x}}dx} = ae^{b} - c$ $I = \int_{1}^{2} (1 + x + \frac{1}{x}) e^{x - \frac{1}{x}} d x = a e^{b} - c$ với $a;b;c\mathbb{\in R}$ $a; b; c \in R$ ; $a \neq 0$ $a \neq 0$ . Lúc này $S = a + b + c$ có giá trị bằng:

A. $S = - \frac{1}{2}$

S = - \frac{1}{2}

B. $S = - \frac{3}{2}$

S = - \frac{3}{2}

C. $S = \frac{1}{3}$

S = \frac{1}{3}

D. $S = \dfrac{9}{2}$

S = \frac{9}{2}

Đáp án D.

Lời giải

Ta có $I = \int_{1}^{2}{\left( 1 + x + \frac{1}{x} \right)e^{x - \frac{1}{x}}}dx = \int_{1}^{2}{e^{x - \frac{1}{x}}dx} + \int_{1}^{2}{\left( x + \frac{1}{x} \right)e^{x - \frac{1}{x}}dx}$ $I = \int_{1}^{2} (1 + x + \frac{1}{x}) e^{x - \frac{1}{x}} d x = \int_{1}^{2} e^{x - \frac{1}{x}} d x + \int_{1}^{2} (x + \frac{1}{x}) e^{x - \frac{1}{x}} d x$ (1)

Đặt $I_{1} = \int_{1}^{2}{e^{x - \frac{1}{x}}dx}$ $I_{1} = \int_{1}^{2} e^{x - \frac{1}{x}} d x$ .

Đặt $\left\{ \begin{matrix} u = e^{x - \frac{1}{x}} \Rightarrow du = \left( 1 + \frac{1}{x^{2}} \right)e^{x - \frac{1}{x}}dx \\ dv = dx \Rightarrow v = x \\ \end{matrix} \right.$ ${\begin{matrix} u = e^{x - \frac{1}{x}} \Rightarrow d u = (1 + \frac{1}{x^{2}}) e^{x - \frac{1}{x}} d x \\ d v = d x \Rightarrow v = x \end{matrix}$

Theo công thức tích phân từng phần ta có $I_{1} = \left. \ xe^{x - \frac{1}{x}} \right|_{1}^{2} - \int_{1}^{2}{\left( x + \frac{1}{x} \right)e^{x - \frac{1}{x}}dx}$ $I_{1} = {x e^{x - \frac{1}{x}} |}_{1}^{2} - \int_{1}^{2} (x + \frac{1}{x}) e^{x - \frac{1}{x}} d x$ (2)

Từ (1); (2) ta có

$I = \left. \ x.e^{x - \frac{1}{x}} \right|_{1}^{2} - \int_{1}^{2}{\left( x + \frac{1}{x} \right)e^{x - \frac{1}{x}}dx} + \int_{1}^{2}{\left( x + \frac{1}{x} \right)e^{x - \frac{1}{x}}dx}$ $I = {x . e^{x - \frac{1}{x}} |}_{1}^{2} - \int_{1}^{2} (x + \frac{1}{x}) e^{x - \frac{1}{x}} d x + \int_{1}^{2} (x + \frac{1}{x}) e^{x - \frac{1}{x}} d x$

$= \left. \ x.e^{x - \frac{1}{x}} \right|_{1}^{2} = 2.e^{2 - \frac{1}{2}} - 1.e^{1 - \frac{1}{1}} = 2.e^{\frac{3}{2}} - 1$ $= {x . e^{x - \frac{1}{x}} |}_{1}^{2} = 2. e^{2 - \frac{1}{2}} - 1. e^{1 - \frac{1}{1}} = 2. e^{\frac{3}{2}} - 1$

$\Rightarrow a = 2;b = \frac{3}{2};c = 1 \Rightarrow a + b + c = \frac{9}{2}$ $\Rightarrow a = 2; b = \frac{3}{2}; c = 1 \Rightarrow a + b + c = \frac{9}{2}$ .

Nhận xét: Ta thấy trong bài toán bên việc sử dụng tích phân từng phần ở đây rất thông minh khi phát hiện được $\left( x - \frac{1}{x} \right)^{/} = 1 +\frac{1}{x^{2}}$ ${(x - \frac{1}{x})}^{/} = 1 + \frac{1}{x^{2}}$ khi nhân thêm x sẽ triệt tiêu được $\int_{1}^{2}{\left( x + \frac{1}{x} \right)e^{x - \frac{1}{x}}dx}$ $\int_{1}^{2} (x + \frac{1}{x}) e^{x - \frac{1}{x}} d x$ .

Xem thêm các bài Tìm bài trong mục này khác:

Chia sẻ, đánh giá bài viết

1

3

Bài trước

Bài sau

Chia sẻ bởi:
Su kem

Tải về

Chọn file muốn tải về:

Tích phân là gì? Khái niệm và các tính chất tích phân dễ hiểu nhất

409,2 KB

File Word

Đóng Chỉ thành viên VnDoc PRO/PROPLUS tải được nội dung này!

Đóng

79.000 / tháng

Mua ngay

Đặc quyền các gói Thành viên

PRO

Phổ biến nhất

PRO+

Tải tài liệu Cao cấp 1 Lớp

Tải tài liệu Trả phí + Miễn phí

Xem nội dung bài viết

Trải nghiệm Không quảng cáo

Làm bài trắc nghiệm không giới hạn

Tìm hiểu thêm

Mua cả năm Tiết kiệm tới 48%

Xác thực tài khoản!

Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:

Số điện thoại chưa đúng định dạng!

Sắp xếp theo

Xóa Đăng nhập để Gửi

Tìm bài trong mục này

Gợi ý cho bạn

Xem thêm

Chuyên đề Toán 12

Xem thêm

Mầm non

Lớp 1

Lớp 2

Lớp 3

Lớp 4

Lớp 5

Lớp 6

Lớp 7

Lớp 8

Lớp 9

Lớp 10

Lớp 11

Lớp 12

Thi vào lớp 6

Thi vào lớp 10

Thi Tốt Nghiệp THPT

Đánh Giá Năng Lực

Khóa Học Trực Tuyến

Hỏi bài

Trắc nghiệm Online

Tiếng Anh

Thư viện Học liệu

Bài tập Cuối tuần

Bài tập Hàng ngày

Thư viện Đề thi

Giáo án - Bài giảng

Tất cả danh mục

Giáo án STEAM

Dạy con học

Giáo án

Trường mầm non

Danh mục Trường Tiểu học

Sáng kiến kinh nghiệm

Thư viện Đề thi

Bài tập cuối tuần

Trắc nghiệm

Sách Cánh diều

Sách Chân trời sáng tạo

Sách Kết nối tri thức

Tài liệu Giáo viên

Thư viện Đề thi

Bài tập Hàng ngày

Bài tập Cuối tuần

Trắc nghiệm

Môn Toán lớp 2

Môn Tiếng Việt lớp 2

Chuyên đề - Văn mẫu

Môn Tiếng Anh

Tài liệu Giáo viên

Thư viện Đề thi

Bài tập Hàng ngày

Bài tập Cuối tuần

Trắc nghiệm

Môn Toán lớp 3

Môn Tiếng Việt lớp 3

Chuyên đề - Văn mẫu

Tiếng Anh lớp 3

Tài liệu Giáo viên

Thư viện Đề thi

Bài tập Hàng ngày

Bài tập Cuối tuần

Trắc nghiệm

Môn Toán lớp 4

Môn Tiếng Việt lớp 4

Tiếng Anh lớp 4

Tài liệu Giáo viên

Thư viện Đề thi

Bài tập Hàng ngày

Bài tập Cuối tuần

Trắc nghiệm

Môn Toán lớp 5

Môn Tiếng Việt lớp 5

Môn Tiếng Anh 5

Thi vào lớp 6

Tài liệu Giáo viên

Ôn thi

Thư Viện Đề Thi

Trắc nghiệm

Khóa Học Trực Tuyến

Môn Toán