Giao diện mới của VnDoc Pro: Dễ sử dụng hơn - chỉ tập trung vào lớp bạn quan tâm. Vui lòng chọn lớp mà bạn quan tâm: Lưu và trải nghiệm
Đóng
Điểm danh hàng ngày
  • Hôm nay +3
  • Ngày 2 +3
  • Ngày 3 +3
  • Ngày 4 +3
  • Ngày 5 +3
  • Ngày 6 +3
  • Ngày 7 +5
Bạn đã điểm danh Hôm nay và nhận 3 điểm!
Nhắn tin Zalo VNDOC để nhận tư vấn mua gói Thành viên hoặc tải tài liệu Hotline hỗ trợ: 0936 120 169
VnDoc.com Lớp 12 Toán 12 Chuyên đề Toán 12
Đóng
Bạn đã dùng hết 1 lần làm bài Trắc nghiệm miễn phí. Mời bạn mua tài khoản VnDoc PRO để tiếp tục! Tìm hiểu thêm
Mua VnDoc PRO chỉ từ 79.000đ

Bài tập Xác suất toàn phần Công thức Bayes Mức độ Nhận Biết

Chuyên đề Toán 12 có đáp án

Xác suất toàn phần công thức Bayes toán 12

Bạn đang ôn thi THPT Quốc gia và muốn nắm vững kiến thức về xác suất toàn phần và công thức Bayes? Trong chuyên đề toán lớp 12, đây là một nội dung quan trọng thường xuất hiện trong các đề thi. Bài viết dưới đây sẽ giúp bạn luyện tập các bài tập xác suất toàn phần, công thức Bayes ở mức độ nhận biết, với lời giải chi tiết, dễ hiểu và sát chương trình học. Đây là tài liệu không thể thiếu dành cho học sinh lớp 12 đang chuẩn bị bước vào kỳ thi quan trọng!

Nhận biết Thông hiểu Vận dụng Vận dụng cao
  • Bài kiểm tra này bao gồm 24 câu
  • Điểm số bài kiểm tra: 24 điểm
  • Xem lại kỹ lý thuyết trước khi làm bài
  • Chuẩn bị giấy và bút để nháp trước khi bắt đầu
Bắt đầu!!
00:00:00
  • Câu 1: Nhận biết
    Tính xác suất cỉa biến cố A

    Cho hai biến cố A và B biết P(B) = 0,6\ ;\ \ P\left( A|B \right) = 0,3\ ;\ \ P\left( A|\overline{B} \right) = 0,8. Tính P(A)

    Hướng dẫn:

    Ta có:

    P\left( \overline{B} \right) = 1 - P(B) = 0,4

    \Rightarrow P(A) = P(B).P\left( A|B \right) + P\left( \overline{B} \right).P\left( A|\overline{B} \right)

    = 0,6.0,3 + 0,4.0,8 = 0,5

  • Câu 2: Nhận biết
    Tính P(B)

    Xét một phép thử có biến cố A và B. Biết xác suất xảy ra các biến cố P(A), P\left( B|A \right), P\left( B|\overline{A} \right) được thể hiện trong sơ đồ sau:

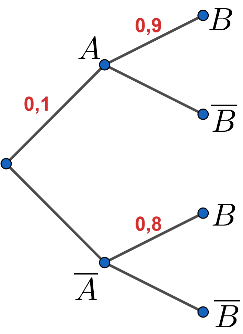
    Tính P(B).

    Hướng dẫn:

    Ta có

    P(B) = P(A)P\left( B|A \right) + P\left( \overline{A} \right)P\left( B|\overline{A} \right)

    = 0,1 \cdot 0,9 + (1 - 0,1) \cdot 0,8 = 0,81.

  • Câu 3: Nhận biết
    Tính xác suất của biến cố B

    Cho sơ đồ hình cây như sau

    Tính xác suất của biến cố B.

    Hướng dẫn:

    Ta có P(B) = 0,4.0,6 + 0,4.0,3 = 0,36.

  • Câu 4: Nhận biết
    Tính P(A)

    Cho hai biến cố A,\ B thỏa mãn P\left( \overline{B} \right) = 0,2;\ P\left( A|B \right) = 0,5;\ P\left( \left. \ A \right|\overline{B} \right) = 0,3. Khi đó, P(A) bằng

    Hướng dẫn:

    Ta có: P(B) = 1 - P\left( \overline{B} \right) = 0,8.

    Theo công thức xác suất toàn phần, ta có:

    P(A) = P(B).P\left( A|B \right) + P\left( \overline{B} \right).P\left( A|\overline{B} \right)

    = 0,8.0,5 + 0,2.0,3 = 0,46.

  • Câu 5: Nhận biết
    Tính giá trị của P(A)

    Cho hai biến cố A và B, với P(B) = 0,8, P\left( A|B \right) = 0,7, P\left( A|\overline{B} \right) = 0,45. Giá trị P(A) bằng

    Hướng dẫn:

    Ta có: P\left( \overline{B} \right) = 1 - P(B) = 1 - 0,8 = 0,2

    Công thức xác suất toàn phần

    P(A) = P(B).P\left( A|B \right) + P\left( \overline{B} \right).P\left( A|\overline{B} \right)= 0,8.0,7 + 0,2.0,45 = 0,65

  • Câu 6: Nhận biết
    Tính P(B|A)

    Cho hai biến cố A,B thỏa mãn P(A) = 0,4, P(B) = 0,3, P(A|B) = 0,25. Khi đó, P(B|A) bằng

    Hướng dẫn:

    Theo công thức Bayes, ta có:

    P(B|A) = \frac{P(B).P(A|B)}{P(A)} = \frac{0,3.0,25}{0,4} = 0,1875.

  • Câu 7: Nhận biết
    Tính P(A|B)

    Cho hai biến cố A và B với P(A) = 0,2; P(B) = 0,26; P\left( B|A \right) = 0,7. Tính P\left( A|B \right).

    Hướng dẫn:

    Ta có: P\left( A|B \right) = \frac{P(A).P\left( B|A \right)}{P(B)} = \frac{0,2.0,7}{0,26} = \frac{7}{13}.

  • Câu 8: Nhận biết
    Xác định giá trị P(A)

    Cho hai biến cố A và B với P(B) = 0,8, P\left( A|B \right) = 0,7, P\left( A|\overline{B} \right) = 0,45. Tính P(A).

    Hướng dẫn:

    Ta có P\left( \overline{B} \right) = 1 - P(B) = 1 - 0,8 = 0,2.

    Công thức xác suất toàn phần:

    P(A) = P(B).P\left( A|B \right) + P\left(\overline{B} \right).P\left( A|\overline{B} \right)

    = 0,8.0,7 + 0,2.0,45= 0,65.

  • Câu 9: Nhận biết
    Tính P(B|A)

    Cho hai biến cố A và B, với P(B) = 0,8, P\left( A|B \right) = 0,7, P\left( A|\overline{B} \right) = 0,45. Tính P\left( B|A \right).

    Hướng dẫn:

    Ta có: P\left( \overline{B} \right) = 1 - 0,8 = 0,2.

    Công thức Bayes:

    P\left( B|A \right) = \frac{P(B)P\left( A|B \right)}{P(B)P\left( A|B \right) + P\left( \overline{B} \right)P\left( A|\overline{B} \right)}

    \Rightarrow P\left( B|A \right) = \frac{0,8.0,7}{0,8.0,7 + 0,2.0,45} = \frac{56}{65}.

  • Câu 10: Nhận biết
    Tính P(A|B)

    Cho hai biến cố A và B là hai biến cố độc lập, với P(A) = 0,2, P(B) = 0,4. Tính P\left( A|B \right).

    Hướng dẫn:

    Ta có:

    A và B là hai biến cố độc lập nên: P\left( A|B \right) = P(A) = 0,2.

  • Câu 11: Nhận biết
    Tính P(A|B)

    Cho P(A) = 0,3; P(B) = 0,5; P\left( B\left| A \right.\ \right) = 0,7. Khi đó P\left( A\left| B \right.\ \right) bằng

    Hướng dẫn:

    Theo công thức Bayes, ta có:

    P\left( A\left| B \right.\ \right) = \frac{P(A).P\left( B\left| A \right.\ \right)}{P(B)} = \frac{0,3.0,7}{0,5} = 0,42.

  • Câu 12: Nhận biết
    Chọn đáp án đúng

    Cho hai biến cố A và B. Biết P(B) = 0,01; P\left( A|B \right) = 0,7; P\left( A|\overline{B} \right) = 0,09. Khi đó P(A) bằng

    Hướng dẫn:

    Ta có: P(B) = 0,01 \Rightarrow P\left( \overline{B} \right) = 1 - 0,01 = 0,99.

    Theo công thức xác suất toàn phần, ta có:

    P(A) = P(B)P\left( A|B \right) + P\left( \overline{B} \right)P\left( A|\overline{B} \right)

    = 0,01.0,7 + 0,99.0,09 = 0,0961.

  • Câu 13: Nhận biết
    Chọn đáp án đúng

    Cho hai biến cố A và B, công thức tính xác suất toàn phần là

    Hướng dẫn:

    Ta có: P(A) = P(B).P\left( A|B \right) + P\left( \overline{B} \right).P\left( A|\overline{B} \right)

  • Câu 14: Nhận biết
    Kết luận đúng

    Giả sử A và B là hai biến cố ngẫu nhiên thỏa mãn P(A) > 0 và 0 < P(B) < 1. Khi đó

    Hướng dẫn:

    Ta có: P\left( \left. \ B \right|A \right) = \frac{P(B)P\left( \left. \ A \right|B \right)}{P(B)P\left( \left. \ A \right|B \right) + P\left( \overline{B} \right)P\left( \left. \ A \right|\overline{B} \right)}

  • Câu 15: Nhận biết
    Xác định câu đúng

    Chọn khẳng định đúng.

    Hướng dẫn:

    Câu đúng là : « Với hai biến cố A,B mà P(A) > 0,P(B) > 0, ta có:

    P(B|A) = \frac{P(B).P(A|B)}{P(A)}”

  • Câu 16: Nhận biết
    Chọn công thức đúng

    Cho hai biến cố A và B là hai biến cố ngẫu nhiên màP(A) > 0,P(B) > 0, công thức Bayes là:

    Hướng dẫn:

    Ta có: P\left( B|A \right) = \frac{P(B).P\left( A|B \right)}{P(A)}.

  • Câu 17: Nhận biết
    Tìm khẳng định sai

    Giả sử A và B là hai biến cố ngẫu nhiên thỏa mãn P(A) > 0 và 0 < P(B) < 1. Khẳng định nào dưới đây sai?

    Hướng dẫn:

    Giả sử A và B là hai biến cố ngẫu nhiên thỏa mãn P(A) > 0 và 0 < P(B) < 1.

    Khi đó, công thức Bayes:

    P\left( B|A \right) = \frac{P(B)P\left( A|B \right)}{P(B)P\left( A|B \right) + P\left( \overline{B} \right)P\left( A|\overline{B} \right)}

    Hay còn có thể viết dưới dạng: P\left( B|A \right) = \frac{P(B)P\left( A|B \right)}{P(A)}.

  • Câu 18: Nhận biết
    Tính P(A|B)

    Cho hai biến cố A và B, với P(A) = 0,2, P(B) = 0,26, P\left( B|A \right) = 0,7. Tính P\left( A|B \right).

    Hướng dẫn:

    Theo công thức Bayes, ta có

    P\left( A|B \right) = \frac{P(A).P\left( B|A \right)}{P(B)} = \frac{0,2.0,7}{0,26} = \frac{7}{13}.

  • Câu 19: Nhận biết
    Chọn đáp án đúng

    Cho hai biến cố A và B sao cho P(A) = 0,6; P(B) = 0,4; P\left( A|B \right) = 0,3. Khi đó P\left( B|A \right) bằng?

    Hướng dẫn:

    Áp dụng công thức Bayes, ta có:

    P\left( B|A \right) = \frac{P(B)P\left( A|B \right)}{P(A)} = \frac{0,4.0,3}{0,6} = 0,2.

  • Câu 20: Nhận biết
    Xác định giá trị P(A)

    Nếu hai biến cố A, B thỏa mãn P(B) = 0,6;\ P\left( A\left| B \right.\ \right) = 0,5;P\left( A\left| \overline{B} \right.\ \right) = 0,3 thì P(A) bằng:

    Hướng dẫn:

    Ta có:

    P(A) = P(B).P\left( A\left| B \right.\ \right) + P\left( \overline{B} \right).P\left( A\left| \overline{B} \right.\ \right)

    = 0,6.0,5 + 0,4.0,3 = 0,42

  • Câu 21: Nhận biết
    Chọn đáp án đúng

    Cho hai biến cố A và B với 0 < P(B) < 1. Khi đó

    Hướng dẫn:

    Ta có: P(A) = P(B)P\left( \left. \ A \right|B \right) + P\left( \overline{B} \right)P\left( \left. \ A \right|\overline{B} \right)

  • Câu 22: Nhận biết
    Tính P(A)

    Cho hai biến cố A,B với P(B) = 0,6, P(A|B) = 0,7 và P(A|\overline{B}) = 0,4. Khi đó P(A) bằng

    Hướng dẫn:

    Ta có: P(\overline{B}) = 1 - P(B) = 1 - 0,6 = 0,4.

    Theo công thức xác suất toàn phần:

    P(A) = P(B).P\left( A \middle| B \right) + P\left( \overline{B} \right).P\left( A \middle| \overline{B} \right)

    = 0,6.0,7 + 0,4.0,4 = 0,58.

  • Câu 23: Nhận biết
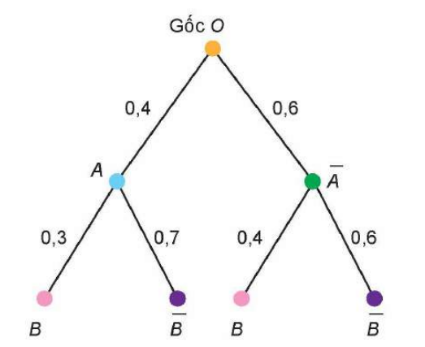
    Tính xác suất của biến cố

    Cho hai biến cố A,B sao cho P(A) = 0,3; P(B) = 0,6 và P(A|B) = 0,2. Tính P(B|A).

    Hướng dẫn:

    Ta có P(B|A) = \frac{P(B).P(A|B)}{P(A)} = \frac{0,6.0,2}{0,3} = \frac{2}{5}.

  • Câu 24: Nhận biết
    Tìm P(A)

    Cho 2 biến cố A và B, tìm P(A) biết P\left( A|B \right) = 0,8; P\left( A|\overline{B} \right) = 0,3; P(B) = 0,4.

    Hướng dẫn:

    Ta có:

    P(B) = 0,4 \Rightarrow P\left( \overline{B} \right) = 1 - 0,4 = 0,6.

    Theo công thức xác suất toàn phần:

    P(A) = P(B).P\left( A|B \right) + P\left( \overline{B} \right).P\left( A|\overline{B} \right)

    \Leftrightarrow P(A) = 0,4.0,8\ + 0,6.0,3 = 0,5.

0/24
24 câu:
Kiểm tra Kiểm tra lại Bỏ qua Nộp bài

Chúc mừng Bạn đã hoàn thành bài!

Kết quả làm bài:
  • Nhận biết (100%):
    2/3
  • Thời gian làm bài: 00:00:00
  • Số câu làm đúng: 0
  • Số câu làm sai: 0
  • Điểm số: 0
  • Điểm thưởng: 0
Làm lại
Bạn còn 1 lượt làm bài tập miễn phí. Hãy mua tài khoản VnDoc PRO để học không giới hạn nhé! Bạn đã HẾT lượt làm bài tập miễn phí! Hãy mua tài khoản VnDoc PRO để làm Trắc nghiệm không giới hạn và tải tài liệu nhanh nhé! Mua ngay
1
33 Bài viết đã được lưu
Xác thực tài khoản!

Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:

Số điện thoại chưa đúng định dạng!
Số điện thoại này đã được xác thực!
Bạn có thể dùng Sđt này đăng nhập tại đây!
Lỗi gửi SMS, liên hệ Admin
Sắp xếp theo
Xóa Đăng nhập để Gửi
Tìm bài trong mục này
🖼️

Chuyên đề Toán 12
Xem thêm