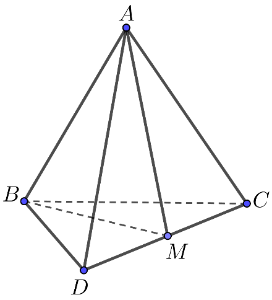
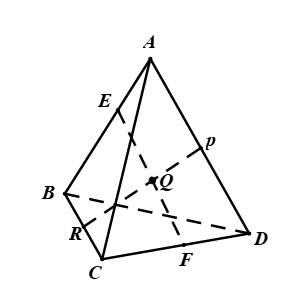
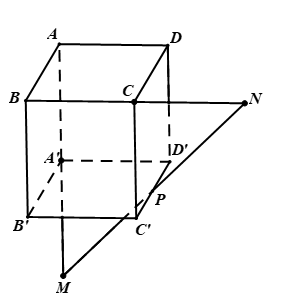
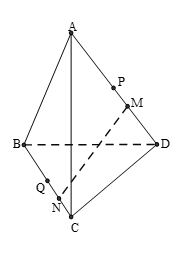
Cho hình chóp . Gọi
là giao điểm của
và
. Trong các khẳng định sau, khẳng định nào sai?
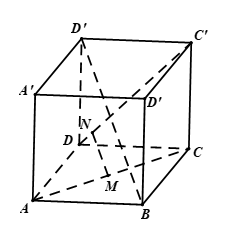
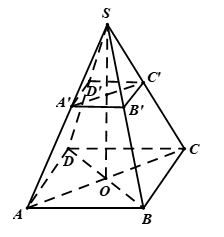
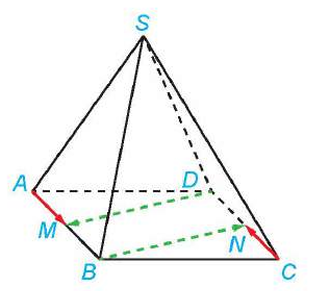
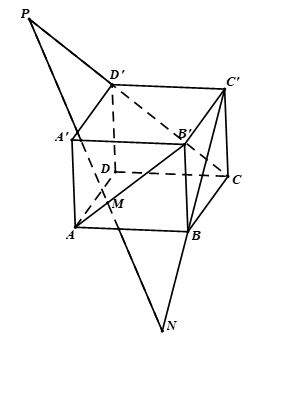
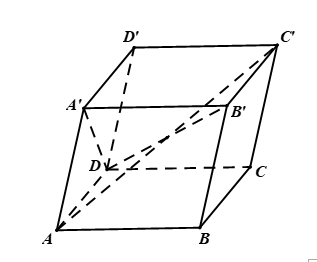
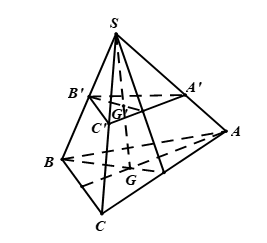
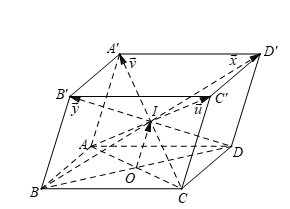
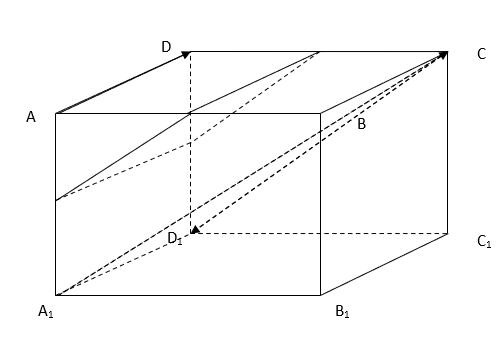
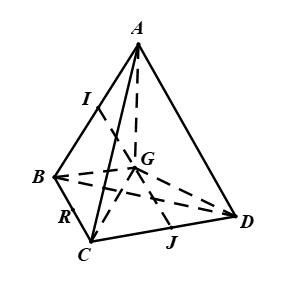
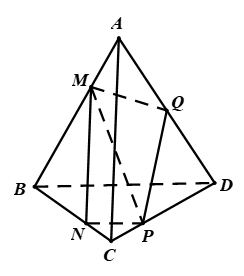
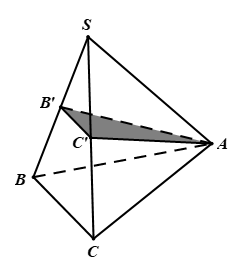
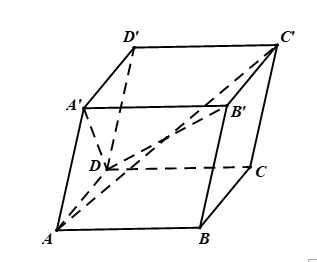
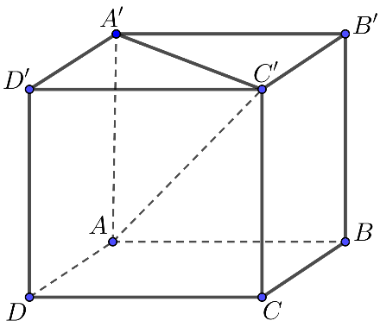
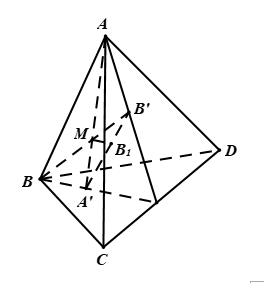
Hình vẽ minh họa
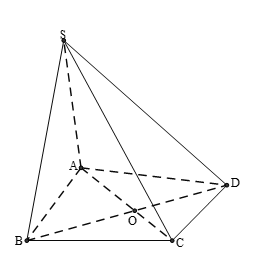
“Nếu thì
là hình thang » Đúng
Vì và
.
Vì và
thẳng hàng nên đặt
.
Mà không cùng phương nên
và
“Nếu là hình bình hành thì
.“. Đúng.
Hs tự biến đổi bằng cách chêm điểm vào vế trái.
“Nếu là hình thang thì
. ». Sai.
Vì nếu là hình thang cân có 2 đáy là
thì sẽ sai.
“Nếu thì
là hình bình hành ». Đúng.
Tương tự đáp án A với là trung điểm 2 đường chéo.