Bài toán về quỹ tích - Vị trí tương đối
Phương pháp giải bài toán quỹ tích hình học không gian
Bài viết Bài toán về quỹ tích – vị trí tương đối được xây dựng nhằm giúp học sinh hệ thống hóa kiến thức cốt lõi, nhận diện các dạng toán tiêu biểu, đồng thời cung cấp phương pháp giải hiệu quả kèm theo ví dụ minh họa. Thông qua việc học tập và luyện tập chuyên đề này, học sinh lớp 12 có thể nâng cao tư duy hình học, cải thiện kỹ năng giải toán và tự tin hơn khi tiếp cận các câu hỏi vận dụng – vận dụng cao trong đề thi THPT Quốc gia.
A. Đặc điểm dạng toán và phương pháp giải toán
Đặc điểm dạng toán:
Những bài toán cần biện luận theo tham số hoặc biến đổi đại số hay xét vị trí tương đối để tìm GTLN, GTNN hoặc tính toán khác. Ở đây chúng ta chỉ xét đơn lẻ các khoảng cách (Nếu có), mà không phải tổng - hiệu các khoảng cách. Phần sau ta sẽ nghiên cứu bài toán “Định luật phản xạ ánh sáng đối với gương phẳng”.
Phương pháp giải:
Tâm tỉ cự là điểm mà chúng ta cũng cần lưu ý. Ngoài ra ta còn vẽ các yếu tố phụ để giải toán: Các yếu tố thường cần vẽ là vuông góc, song song, đối xứng, bằng nhau. Tương ứng với các yếu tố đó là các tính chất hình học của một số hình; lập các phương trình đường; tìm giao điểm; . . .
B. Bài tập ví dụ minh họa bài toán quỹ tích, vị trí tương đối
Ví dụ 1. Trong không gian với hệ toạ độ ![]() cho mặt phẳng
cho mặt phẳng ![]() và các điểm
và các điểm ![]() ;
;![]() . Viết phương trình đường thẳng
. Viết phương trình đường thẳng ![]() nằm trong mặt phẳng
nằm trong mặt phẳng ![]() đi qua
đi qua ![]() và cách
và cách ![]() một khoảng lớn nhất.
một khoảng lớn nhất.
A.  B.
B.  C.
C.  D.
D.
Hướng dẫn giải
Chọn D.
Gọi K là hình chiếu vuông góc của B trên d, ta có ![]() nên khoảng cách lớn nhất khi d vuông góc với BA, d nằm trong
nên khoảng cách lớn nhất khi d vuông góc với BA, d nằm trong ![]() , suy ra
, suy ra ![]() .
.
MENU 9 1 2 nhập ![]() và
và ![]() ta có x = 7, y = -2 nên
ta có x = 7, y = -2 nên ![]() .
.
Ví dụ 2. Cho mặt cầu ![]() và hai điểm
và hai điểm ![]() . Gọi
. Gọi ![]() là mặt phẳng chứa A, B và khoảng cách từ tâm I đến mặt phẳng
là mặt phẳng chứa A, B và khoảng cách từ tâm I đến mặt phẳng ![]() lớn nhất. Viết phương trình mặt phẳng
lớn nhất. Viết phương trình mặt phẳng ![]() .
.
A. ![]() . B.
. B. ![]() .
.
C. ![]() . D.
. D. ![]() .
.
Hướng dẫn giải
Gọi H và K lần lượt là hình chiếu vuông góc của tâm I lên mp(P) và đường thẳng AB, ta có ![]() nên IH lớn nhất bằng IK hay
nên IH lớn nhất bằng IK hay ![]() .
.
Tọa độ điểm I(- 4; 3; 2), ![]() (2; 0; 3).
(2; 0; 3).
Ghi ![]() CALC (nhập tọa độ
CALC (nhập tọa độ ![]() )
) ![]() Sto M
Sto M
ghi ![]() bấm
bấm ![]() ta có
ta có ![]() .
.
Phương trình (P) là: 3x - y - 2z + 5 = 0. Chọn A.
Ví dụ 3: Trong không gian ![]() cho hai điểm
cho hai điểm ![]() và
và ![]() Xét khối nón
Xét khối nón ![]() có đỉnh
có đỉnh ![]() đường tròn đáy nằm trên mặt cầu đường kính
đường tròn đáy nằm trên mặt cầu đường kính ![]() Khi
Khi ![]() có thể tích lớn nhất thì mặt phẳng chứa đường tròn đáy của
có thể tích lớn nhất thì mặt phẳng chứa đường tròn đáy của ![]() có phương trình dạng
có phương trình dạng ![]() Giá trị của
Giá trị của ![]() bằng
bằng
A.![]() B.
B.![]() C.
C.![]() D.
D. ![]()
Hướng dẫn giải
Hình vẽ minh họa
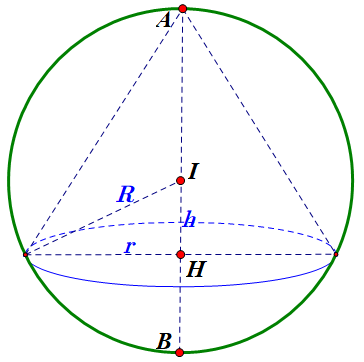
Gọi ![]() , r là bán kính đáy nón,
, r là bán kính đáy nón, ![]() là bán kính mặt cầu.
là bán kính mặt cầu.
Ta có ![]() và thể tích khối nón là:
và thể tích khối nón là: ![]() .
.
Ta có : ![]()
![]() .
.
Dấu bằng có khi ![]() .
.
Mặt phẳng (P) chứa đường tròn đáy của nón có ![]() .
.
Đặt ![]() suy ra
suy ra ![]() .
.
Phương trình (P) là: ![]() Vậy
Vậy ![]() Chọn D.
Chọn D.
Ví dụ 4. Trong không gian Oxyz, cho mặt cầu ![]() và đường thẳng
và đường thẳng ![]() . Mặt phẳng
. Mặt phẳng ![]() chứa đường thẳng d và cắt mặt cầu
chứa đường thẳng d và cắt mặt cầu ![]() theo giao tuyến là đường tròn có bán kính nhỏ nhất. Phương trình của
theo giao tuyến là đường tròn có bán kính nhỏ nhất. Phương trình của ![]() là
là ![]() . Mệnh đề nào dưới đây đúng ?
. Mệnh đề nào dưới đây đúng ?
A. ![]() . B.
. B. ![]() . C.
. C. ![]() . D.
. D. ![]() .
.
Hướng dẫn giải
Gọi I là tâm mặt cầu, H là tâm đường tròn giao tuyến và là hình chiếu của I trên (P).
Kẻ IK vuông góc với d.
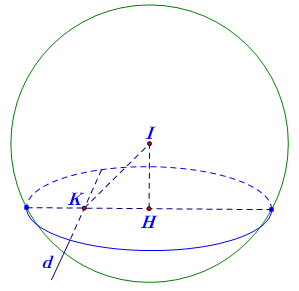
Đường tròn có bán kính nhỏ nhất khi (P) cách xa I nhất, mà ![]() .Vậy ta phải có
.Vậy ta phải có ![]() và (P) có một vtpt
và (P) có một vtpt ![]() .
.
Ghi ![]() CALC (nhập tọa độ I)
CALC (nhập tọa độ I) ![]() STO M
STO M
Ghi ![]() bấm
bấm ![]() ta có tọa độ véc tơ
ta có tọa độ véc tơ ![]()
![]() . Chọn C.
. Chọn C.
Ví dụ 5. Trong không gian ![]() , cho hai điểm
, cho hai điểm ![]() ,
, ![]() và mặt cầu
và mặt cầu ![]() . Mặt phẳng
. Mặt phẳng ![]() đi qua
đi qua ![]() và cắt
và cắt ![]() theo giao tuyến là đường tròn có bán kính nhỏ nhất. Tính
theo giao tuyến là đường tròn có bán kính nhỏ nhất. Tính ![]() ?
?
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]() .
.
Hướng dẫn giải
Gọi ![]() là tâm mặt cầu. Kẻ
là tâm mặt cầu. Kẻ ![]() lần lượt vuông góc với
lần lượt vuông góc với ![]() và
và ![]() thì ta có
thì ta có ![]() , do đó để đường tròn giao tuyến có bán kính nhỏ nhất thì
, do đó để đường tròn giao tuyến có bán kính nhỏ nhất thì ![]() cách xa tâm I nhất, hay
cách xa tâm I nhất, hay ![]() , khi đó
, khi đó ![]() là một VTPT của
là một VTPT của ![]() .
.
Ghi ![]() CALC nhập
CALC nhập ![]() STO M, bấm AC ghi
STO M, bấm AC ghi ![]() bấm
bấm ![]() ta được
ta được ![]() , suy ra
, suy ra ![]() . Chọn A.
. Chọn A.
C. Bài tập tự rèn luyện có hướng dẫn giải chi tiết
Bài tập 1. Trong không gian ![]() , cho mặt cầu
, cho mặt cầu ![]() và điểm
và điểm ![]() . Mặt phẳng
. Mặt phẳng ![]() đi qua
đi qua ![]() và cắt
và cắt ![]() theo đường tròn
theo đường tròn ![]() có chu vi nhỏ nhất. Gọi
có chu vi nhỏ nhất. Gọi ![]() là điểm thuộc đường tròn
là điểm thuộc đường tròn ![]() sao cho
sao cho ![]() . Tính
. Tính ![]() .
.
A. ![]() . B.
. B. ![]() . C.
. C. ![]() . D. 3.
. D. 3.
Bài tập 2. Trong không gian với hệ tọa độ ![]() , cho hai mặt phẳng
, cho hai mặt phẳng ![]() ;
; ![]() . Gọi
. Gọi ![]() là mặt cầu cắt mặt phẳng
là mặt cầu cắt mặt phẳng ![]() theo giao tuyến là đường tròn tâm
theo giao tuyến là đường tròn tâm ![]() , bán kính
, bán kính ![]() và cắt mặt phẳng
và cắt mặt phẳng ![]() theo giao tuyến là đường tròn có bán kính lớn nhất. Phương trình mặt cầu
theo giao tuyến là đường tròn có bán kính lớn nhất. Phương trình mặt cầu ![]() là:
là:
A. ![]() . B.
. B. ![]() .
.
C. ![]() . D.
. D. ![]() .
.
Bài tập 3. Trong không gian với hệ tọa độ ![]() , cho mặt cầu
, cho mặt cầu ![]() có tâm thuộc mặt phẳng
có tâm thuộc mặt phẳng ![]() và đi qua hai điểm
và đi qua hai điểm ![]() ,
, ![]() . Bán kính nhỏ nhất của mặt cầu
. Bán kính nhỏ nhất của mặt cầu ![]() bằng
bằng
A. ![]() . B.
. B. ![]() . C.
. C. ![]() . D.
. D. ![]() .
.
Bài tập 4. Trong không gian với hệ tọa độ ![]() , cho hai điểm
, cho hai điểm ![]() ,
, ![]() và mặt cầu
và mặt cầu ![]() . Tìm giá trị nhỏ nhất của
. Tìm giá trị nhỏ nhất của ![]() để trên
để trên ![]() tồn tại điểm
tồn tại điểm ![]() sao cho
sao cho ![]() .
.
A. ![]() . B.
. B. ![]() . C.
. C. ![]() . D.
. D. ![]() .
.
Bài tập 5. Trong không gian Oxyz, cho điểm ![]() . Xét đường thẳng
. Xét đường thẳng ![]() thay đổi song song với Oz và cách Oz một khoảng bằng 2. Khi khoảng cách từ
thay đổi song song với Oz và cách Oz một khoảng bằng 2. Khi khoảng cách từ ![]() đến
đến ![]() nhỏ nhất,
nhỏ nhất, ![]() đi qua điểm nào dưới đây?
đi qua điểm nào dưới đây?
A. ![]() . B.
. B. ![]() .
.
C. ![]() . D.
. D. ![]() .
.
🔍 Để thuận tiện cho việc học tập và lưu trữ, mời bạn tải tài liệu tham khảo bên dưới.
----------------------------------------------
Chuyên đề bài toán về quỹ tích – vị trí tương đối không chỉ giúp học sinh hiểu sâu hơn về hình học mà còn rèn luyện khả năng tư duy và phân tích bài toán trong chương trình Toán 12. Khi nắm vững khái niệm quỹ tích, xác định đúng vị trí tương đối giữa các đối tượng hình học, học sinh sẽ dễ dàng lựa chọn phương pháp giải phù hợp và hạn chế sai sót trong quá trình làm bài.










