Chuyên đề Tìm giá trị lớn nhất nhỏ nhất của hàm số trên khoảng
Tìm giá trị lớn nhất nhỏ nhất của hàm số Toán 12
Tìm giá trị lớn nhất (GTLN) và giá trị nhỏ nhất (GTNN) của hàm số trên một khoảng là dạng toán quan trọng trong chương trình Toán 12, xuất hiện nhiều trong các đề thi học kỳ và kỳ thi THPT Quốc gia. Chuyên đề này sẽ giúp học sinh nắm vững kiến thức lý thuyết, phương pháp giải nhanh và hiệu quả, kết hợp với hệ thống bài tập có đáp án chi tiết. Đây là tài liệu hữu ích để ôn luyện và nâng cao kỹ năng giải bài tập hàm số từ cơ bản đến nâng cao.
A. Bài tập trắc nghiệm tìm GTLN, GTNN của hàm số
Câu 1: Tìm giá trị nhỏ nhất 
\(m\) của hàm số \(f(x) = x^{2} +
\frac{2}{x}\) trên khoảng \((0; +
\infty).\)
A. \(m = 1.\) B. \(m = 2.\) C . \(m = 3.\) D. \(m = 4.\)
Câu 2: Gọi \(y_{CT}\) là giá trị cực tiểu của hàm số \(f(x) = x^{2} +
\frac{2}{x}\) trên \((0; +
\infty)\). Mệnh đề nào sau đây là đúng?
A. \(y_{CT} > \min_{(0; +
\infty)}y.\) B. \(y_{CT} = 1 + \min_{(0; +
\infty)}y.\)
C. \(y_{CT} = \min_{(0; +
\infty)}y.\) D. \({y_{{\text{CT}}}} < \mathop {\min }\limits_{\left( {0; + \infty } \right)} y.\)
Câu 3: Tìm giá trị lớn nhất \(M\) của hàm số \(f(x) = x - \frac{1}{x}\) trên \((0;3\rbrack.\)
A. \(M = 3.\) B. \(M = \frac{8}{3}\) C. \(M = \frac{3}{8}.\) D. \(m =0.\)
Câu 4: Biết rằng hàm số \(f(x) = - x + 2018
- \frac{1}{x}\) đạt giá trị lớn nhất trên đoạn \((0;4)\) tại \(x_{0}\). Tính \(P
= x_{0} + 2018.\)
A. \(P = 4032.\) B. \(P = 2019.\) C. \(P = 2020.\) D. \(P = 2018.\)
Câu 5: Tính giá trị nhỏ nhất của hàm số \(y
= 3x + \frac{4}{x^{2}}\) trên khoảng \((0; + \infty)\).
A. \(\min_{(0; + \infty)}y =
\frac{33}{5}\) B. \(\min_{(0; + \infty)}y =
2\sqrt[3]{9}\) C. \(\min_{(0; + \infty)}y =
3\sqrt[3]{9}\) D. \(\min_{(0; + \infty)}y =
7\)
Câu 6: Gọi \(m\) là giá trị nhỏ nhất của hàm số \(y = x - 1 + \frac{4}{x -
1}\) trên khoảng \((1; +
\infty)\). Tìm \(m\)?
A. \(m = 5\) B. \(m = 4\) C. \(m = 2\) D. \(m = 3\)
Câu 7: Giá trị nhỏ nhất của hàm số \(y = x
- 5 + \frac{1}{x}\) trên khoảng \((0; +
\infty)\) bằng bao nhiêu?
A. 0 B. -1 C. -3 D. -2
Câu 8: Gọi \(m\) là giá trị nhở nhất của hàm số \(y = x + \frac{4}{x}\) trên khoảng \((0; + \infty)\). Tìm \(m\)?
A. \(m = 4\) B. \(m = 2\) C. \(m = 1\) D. \(m = 3\)
Câu 9: Giá trị nhỏ nhất của hàm số \(f(x) =
x + \frac{1}{x}\) trên nửa khoảng \(\lbrack 2; + \infty)\) là:
A. \(2\) B. \(\frac{5}{2}\) C. \(0\) D. \(\frac{7}{2}\)
Câu 10 : Gọi \(m\) là giá trị nhỏ nhất của hàm số \(y = x + \frac{4}{x}\) trên khoảng \((0; + \infty)\). Tìm \(m\) ?
A. \(m = 3\) B. \(m = 4\) C. \(m = 2\) D. \(m = 1\)
Câu 11: Giá trị nhỏ nhất của hàm số \(y =
\sqrt{4 - x} + \sqrt{3}\) trên tập xác định của nó là:
A. \(2 + \sqrt{3}.\) B. \(2\sqrt{3}.\) C. \(0.\) D. \(\sqrt{3}.\)
Câu 12: Với giá trị nào của \(x\) thì hàm số \(y = x^{2} + \frac{1}{x}\) đạt giá trị nhỏ nhất trên khoảng \((0; +
\infty)\)?
A. \(\frac{3}{\sqrt[3]{4}}\) B. \(\frac{1}{\sqrt{2}}\) C. 1 D. \(\frac{1}{\sqrt[3]{2}}\)
Câu 13: Giá trị nhỏ nhất của hàm số \(y = x
+ \frac{2}{x} - \left( 1 + \sqrt{2} \right)^{2}\) trên khoảng \((0; + \infty)\)?
A. không tồn tại. B. \(- 3\) C. \(- 1 + \sqrt{2}\) D. \(0\)
Câu 14: Cho hàm số \(f(x) =
\frac{\sqrt{x^{2} - 1}}{x - 2}\) với \(x\) thuộc \(D = (
- \infty;\ - 1\rbrack \cup \left\lbrack 1;\ \frac{3}{2}
\right\rbrack\). Mệnh đề nào dưới đây đúng?
A. \(\max_{D}f(x) = 0;\min_{D}f(x) = -\sqrt{5}\).
B. \(\max_{D}f(x) = 0\); không tồn tại \(\min_{D}f(x)\).
C. \(\max_{D}f(x) = 0;\ \min_{D}f(x) = -
1\).
D. \(\min_{D}f(x) =0\); không tồn tại \(\max_{D}f(x)\).
Câu 15: Mệnh đề nào sau đây là đúng về hàm số \(y = \frac{x + 1}{\sqrt{x^{2} + 5}}\)trên tập xác định của nó.
A. Hàm số không có giá trị lớn nhất và không có giá trị nhỏ nhất.
B. Hàm số không có giá trị lớn nhất và có giá trị nhỏ nhất.
C. Hàm số có giá trị lớn nhất và giá trị nhỏ nhất.
D. Hàm số có giá trị lớn nhất và không có giá trị nhỏ nhất.
B. Đáp án tổng quan bài tập trắc nghiệm
|
1 - C |
2 - C |
3 - B |
4 - B |
5 - C |
|
6 – B |
7 - C |
8 - A |
9 - B |
10 - B |
|
11 - D |
12 – D |
13 - B |
14 - A |
15 - D |
C. Hướng dẫn chi tiết bài tập trắc nghiệm
Câu 1:
Ta có :
\(f'(x) = 2x - \frac{2}{x^{2}} =
\frac{2\left( x^{3} - 1 \right)}{x^{2}}\)
\(\Rightarrow f'(x) = 0
\Leftrightarrow x = 1 \in (0; + \infty)\)
Lập bảng biến thiên & dựa vào bảng biến thiên ta thấy \(\min_{(0; + \infty)}f(x) = f(1) = 3.\)
Câu 2:
Ta có:
\(f'(x) = 2x - \frac{2}{x^{2}} =
\frac{2x^{3} - 2}{x^{2}}\)
\(\Rightarrow f'(x) = 0
\Leftrightarrow x = 1 \in (0; + \infty)\)
Qua điểm \(x = 1\) thì hàm số đổi dấu từ \('' - ''\) sang \('' + ''\) trong khoảng \((0; + \infty)\).
Suy ra trên khoảng \((0; + \infty)\) hàm số chỉ có một cực trị và là giá trị cực tiểu nên đó cũng chính là giá trị nhỏ nhất của hàm số.
Vậy \(y_{CT} = \min_{(0; +
\infty)}y.\)
Câu 3:
Đạo hàm \(f'(x) = 1 + \frac{1}{x^{2}}
> 0,\ \forall x \in (0;3).\)
Suy ra hàm số \(f(x)\) đồng biến trên \((0;3\rbrack\) nên đạt giá trị lớn nhất tại \(x = 3\) và \(\max_{(0;3\rbrack}f(x) = f(3) =
\frac{8}{3}.\)
Câu 4:
Ta có:
\(f'(x) = - 1 +
\frac{1}{x^{2}}\)
\(\Rightarrow f'(x) = 0
\Leftrightarrow \left\lbrack \begin{matrix}
x = 1 \in (0;4) \\
x = - 1 \notin (0;4) \\
\end{matrix} \right.\)
Lập bảng biến thiên & dựa vào bảng biến thiên ta thấy hàm số đạt giá trị lớn nhất trên \((0;4)\) tại \(x = x_{0} = 1\)
\(\Rightarrow P = 2019\)
Câu 5:
Cách 1:
\(y = 3x + \frac{4}{x^{2}} = \frac{3x}{2}
+ \frac{3x}{2} + \frac{4}{x^{2}} \geq
3\sqrt[3]{\frac{3x}{2}.\frac{3x}{2}.\frac{4}{x^{2}}} =
3\sqrt[3]{9}\)
Dấu 
xảy ra khi \(\frac{3x}{2} = \frac{4}{x^{2}}
\Leftrightarrow x = \sqrt[3]{\frac{8}{3}}\).
Vậy \(\min_{(0; + \infty)}y =
3\sqrt[3]{9}\)
Cách 2:
Xét hàm số \(y = 3x +
\frac{4}{x^{2}}\) trên khoảng \((0; +
\infty)\)
Ta có \(y = 3x + \frac{4}{x^{2}}
\Rightarrow y' = 3 - \frac{8}{x^{3}}\)
Cho \(y' = 0 \Leftrightarrow
\frac{8}{x^{3}} = 3 \Leftrightarrow x^{3} = \frac{8}{3} \Leftrightarrow
x = \sqrt[3]{\frac{8}{3}}\)
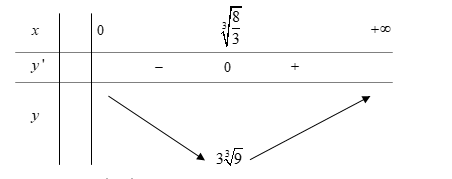
\(\Rightarrow \min_{(0; + \infty)}y =
y\left( \sqrt[3]{\frac{8}{3}} \right) = 3\sqrt[3]{9}\)
Câu 6:
Tập xác định \(D = R\backslash\left\{ 1
\right\}\).
\(y' = \frac{x^{2} - 2x - 3}{(x -
1)^{2}}\ \ ,\ y' = 0 \Leftrightarrow \left\lbrack \begin{matrix}
x = - 1 \\
x = 3 \\
\end{matrix} \right.\).
Bảng biến thiên:
\(\Rightarrow m = \min_{(1; + \ \infty)}y =
4\) khi \(x = 3\)
Câu 7:
Áp dụng bất đẳng thức Cô – si ta có:
\(y = x + \frac{1}{x} - 5 \geq
2\sqrt{x.\frac{1}{x}} - 5 = - 3\)
Dấu bằng xảy ra khi \(x = \frac{1}{x}
\Leftrightarrow x^{2} = 1 \Leftrightarrow x = 1\) (vì \(x > 0\)).
Vậy \(\min_{(0; + \infty)}y = -3\)
------------------------------------------------
Qua chuyên đề “Tìm giá trị lớn nhất nhỏ nhất của hàm số trên khoảng”, các em học sinh lớp 12 sẽ hiểu rõ bản chất của bài toán cực trị, biết cách áp dụng đạo hàm và bảng biến thiên để giải các bài toán tìm GTLN - GTNN một cách chính xác. Hệ thống bài tập có đáp án đi kèm sẽ hỗ trợ việc tự học và ôn luyện hiệu quả tại nhà. Đừng quên kết hợp chuyên đề này với các kiến thức liên quan như khảo sát hàm số, đạo hàm, giới hạn, tiệm cận… để có nền tảng vững chắc cho kỳ thi THPT Quốc gia. Hãy lưu lại bài viết và chia sẻ với bạn bè cùng học nhé!
