VnDoc.com

Tìm giá trị lớn nhất nhỏ nhất của hàm số trên đoạn

Chuyên đề Toán 12 Tìm min max

Bài trước

Tải về

Bài sau

Lớp: Lớp 12

Môn: Toán

Dạng tài liệu: Chuyên đề

Loại File: Word + PDF

Phân loại: Tài liệu Tính phí

GTLN, GTNN của hàm số

A. Giá trị lớn nhất Giá trị nhỏ nhất của hàm số
B. Cách tính giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên một đoạn
C. Một số phương pháp khác tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số

Trong chương trình tích 12, dạng toán tìm giá trị lớn nhất – nhỏ nhất của hàm số trên đoạn là một trong những nội dung quan trọng xuất hiện thường xuyên trong bài kiểm tra, đề thi tốt nghiệp THPT và các kỳ thi đánh giá năng lực. Đây là dạng bài quan trọng giúp học sinh rèn luyện khả năng phân tích các biến thiên của hàm số, hiểu sâu về đạo hàm và vận dụng thành các quy tắc tìm kiếm min , max .

Bài viết này thuộc chuyên mục Chuyên đề Toán 12 Tìm min max, sẽ cung cấp cho bạn kiến trúc cốt lõi, phương pháp giải chuẩn mực và các ví dụ trực quan từ cơ bản đến nâng cao. Với cách trình bày rõ ràng, dễ hiểu và bám sát chương trình GDPT, tài liệu giúp học sinh chắc chắn làm, tránh các lỗi thường gặp và tăng tốc độ xử lý bài toán. Đây là nguồn tài liệu lý tưởng dành cho học sinh thi cuối kỳ, thi tốt nghiệp hoặc luyện thi đại học. Mời các bạn cùng theo dõi bài viết dưới đây nhé.

A. Giá trị lớn nhất Giá trị nhỏ nhất của hàm số

Cho hàm số $y = f(x)$ xác định trên tập $D$.

Số $M$ được gọi là giá trị lớn nhất (GTLN) của hàm số $y = f(x)$ trên tập $D$ nếu $f(x) \leq M$ $f(x) \leq M$ với mọi $x \in D$ $x \in D$ và tồn tại $x_{0} \in D$ $x_{0} \in D$ sao cho $f\left( x_{0} \right) = M$ $f\left( x_{0} \right) = M$

Kí hiệu $M = \max_{D}f(x)$ $M = \max_{D}f(x)$

Số $m$ được gọi là giá trị nhỏ nhất (GTNN) của hàm số $y = f(x)$ trên tập $D$ nếu $f(x) \geq m$ $f(x) \geq m$ với mọi $x \in D$ $x \in D$ và tồn tại $x_{0} \in D$ $x_{0} \in D$ sao cho $f\left( x_{0} \right) = m$ $f\left( x_{0} \right) = m$

Kí hiệu $m = \min_{D}f(x)$ $m = \min_{D}f(x)$

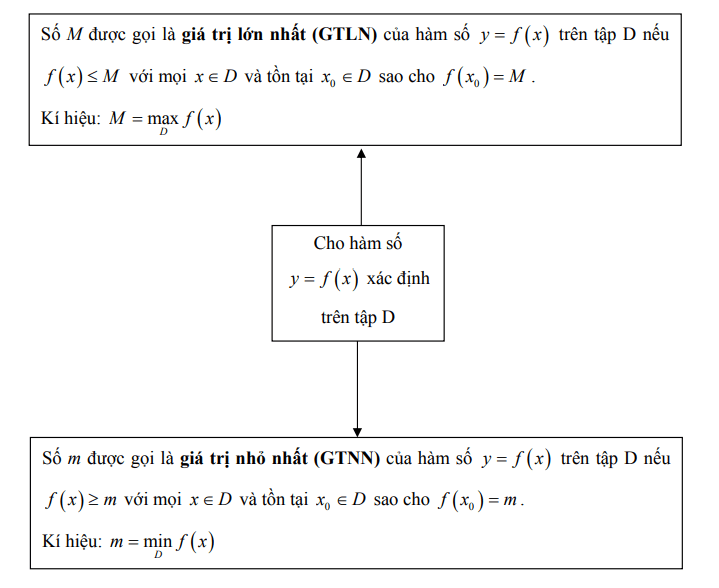
Sơ đồ hệ thống hóa

B. Cách tính giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên một đoạn

Định lí 1.

Mọi hàm số liên tục trên một đoạn đều có giá trị lớn nhất và giá trị nhỏ nhất trên đoạn đó.

Quy tắc tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số liên tục trên một đoạn

Nhận xét: Nếu hàm số $y = f(x)$ có đạo hàm $f'(x)$ giữ nguyên dấu trên đoạn $\lbrack a;b\rbrack$ $\lbrack a;b\rbrack$ thì hàm số đồng biến hoặc nghịch biến trên cả đoạn. Do đó $f(x)$ đạt được giá trị lớn nhất và giá trị nhỏ nhất tại các đầu mút của đoạn đó.

Phương pháp giải

Để tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số $y = f(x)$ trên đoạn $\lbrack a;b\rbrack$ $\lbrack a;b\rbrack$ ta làm như sau.

Bước 1. Tìm $f'(x)$ và tìm các điểm $x_{1};x_{2};...;x_{n}$ $x_{1};x_{2};...;x_{n}$ trên $\lbrack a;b\rbrack$ $\lbrack a;b\rbrack$ mà tại đó $f'(x) = 0$ hoặc $f'(x)$ không xác định.

Bước 2. Tính $f\left( x_{1} \right);f\left( x_{2} \right);...;f\left( x_{n} \right);f(a);f(b)$ $f\left( x_{1} \right);f\left( x_{2} \right);...;f\left( x_{n} \right);f(a);f(b)$

Bước 3. Tìm số lớn nhất M và số nhỏ nhất m trong các số trên. Khi đó:

$M = \max_{\lbrack a;b\rbrack}f(x);m = \min_{\lbrack a;b\rbrack}f(x)$ $M = \max_{\lbrack a;b\rbrack}f(x);m = \min_{\lbrack a;b\rbrack}f(x)$

Chú ý:

Hàm số $y = f(x)$ đồng biến trên $\lbrack a;b\rbrack$ $\lbrack a;b\rbrack$ thì $\left\{ \begin{matrix} \max_{\lbrack a;b\rbrack}f(x) = f(b) \\ \min_{\lbrack a;b\rbrack}f(x) = f(a) \\ \end{matrix} \right.$ $\left\{ \begin{matrix} \max_{\lbrack a;b\rbrack}f(x) = f(b) \\ \min_{\lbrack a;b\rbrack}f(x) = f(a) \\ \end{matrix} \right.$
Hàm số $y = f(x)$ nghịch biến trên $\lbrack a;b\rbrack$ $\lbrack a;b\rbrack$ thì $\left\{ \begin{matrix} \max_{\lbrack a;b\rbrack}f(x) = f(a) \\ \min_{\lbrack a;b\rbrack}f(x) = f(b) \\ \end{matrix} \right.$ $\left\{ \begin{matrix} \max_{\lbrack a;b\rbrack}f(x) = f(a) \\ \min_{\lbrack a;b\rbrack}f(x) = f(b) \\ \end{matrix} \right.$

C. Một số phương pháp khác tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số

Cho hàm số $y = f(x)$

1. Phương pháp tìm miền giá trị

Xem $y = f(x)$ là phương trình đối với ẩn số $x$ và $y$ là tham số.

Tìm điều kiện của y để phương trình $y = f(x)$ có nghiệm.

Từ điều kiện trên, biến đổi đưa đến dạng $m \leq y \leq M$ $m \leq y \leq M$. Xét dấu “=” xảy ra và kết luận.

2. Phương pháp đạo hàm

Khảo sát sự biến thiên của hàm số $y = f(x)$

Dựa vào bảng biến thiên để kết luận.

3. Phương pháp dùng bất đẳng thức

Bất đẳng thức AM – GM

Cho hai số thực không âm

$a + b \geq 2\sqrt{ab}$ $a + b \geq 2\sqrt{ab}$

$\Leftrightarrow 4ab \leq (a + b)^{2} \Leftrightarrow (a + b)^{2} \geq 0$ $\Leftrightarrow 4ab \leq (a + b)^{2} \Leftrightarrow (a + b)^{2} \geq 0$

Bất đẳng thức Cauchy - Schwarz

$\frac{1}{x} + \frac{1}{y} \geq \frac{4}{x + y}$ $\frac{1}{x} + \frac{1}{y} \geq \frac{4}{x + y}$

Bất đẳng thức Bunhiacopxki

Cho các số thực a, b, c, d

$(ax + by)^{2} \leq \left( a^{2} + b^{2} \right)\left( x^{2} + y^{2} \right)$ $(ax + by)^{2} \leq \left( a^{2} + b^{2} \right)\left( x^{2} + y^{2} \right)$

Dấu “=” xảy ra khi $\frac{a}{x} = \frac{b}{y}$ $\frac{a}{x} = \frac{b}{y}$

Một số bổ đề cơ bản

$xy \leq \frac{(x + y)^{2}}{4} \leq \frac{x^{2} + y^{2}}{4}$ $xy \leq \frac{(x + y)^{2}}{4} \leq \frac{x^{2} + y^{2}}{4}$ và $x^{2} + xy + y^{2} \geq \frac{3}{4}(x + y)^{2}$ $x^{2} + xy + y^{2} \geq \frac{3}{4}(x + y)^{2}$
$x^{3} + y^{3} \geq \frac{(x + y)\left( x^{2} + y^{2} \right)}{2} \geq \frac{(x + y)^{3}}{4} \geq xy(x + y)$ $x^{3} + y^{3} \geq \frac{(x + y)\left( x^{2} + y^{2} \right)}{2} \geq \frac{(x + y)^{3}}{4} \geq xy(x + y)$

Ví dụ: a. Xác định giá trị lớn nhất của hàm số $f(x) = x^{3} - 3x + 2$ $f(x) = x^{3} - 3x + 2$ trên đoạn $\lbrack - 1;3\rbrack$ $\lbrack - 1;3\rbrack$?

b. Tìm giá trị nhỏ nhất của hàm số $y = x^{2} + \frac{8}{x}$ $y = x^{2} + \frac{8}{x}$ trên đoạn $\left\lbrack \frac{1}{2};2 \right\rbrack$ $\left\lbrack \frac{1}{2};2 \right\rbrack$?

c. Trên đoạn $\lbrack 0;1\rbrack$ $\lbrack 0;1\rbrack$ hàm số $y = \sqrt{4 - 3x}$ $y = \sqrt{4 - 3x}$ có giá trị nhỏ nhất bằng bao nhiêu?

d. Tính tổng giá trị lớn nhất và giá trị nhỏ nhất của hàm số $y = x^{3} - 3x$ $y = x^{3} - 3x$ trên $\lbrack 1;2\rbrack$ $\lbrack 1;2\rbrack$?

Hướng dẫn giải

a. Ta có: $f'(x) = 3x^{2} - 3$

$\Rightarrow f$ $\Rightarrow f'(x) = 0 \Leftrightarrow 3x^{2} - 3 = 0 \Leftrightarrow \left\lbrack \begin{matrix} x = 1 \in \lbrack - 1;3\rbrack \\ x = - 1 \in \lbrack - 1;3\rbrack \\ \end{matrix} \right.$

Ta có: $\left\{ \begin{matrix} f( - 1) = 4 \\ f(1) = 0 \\ f(3) = 20 \\ \end{matrix} \right.\ \Rightarrow \underset{\lbrack - 1;3\rbrack}{\max f(x)} = 20 \Leftrightarrow x = 3$ $\left\{ \begin{matrix} f( - 1) = 4 \\ f(1) = 0 \\ f(3) = 20 \\ \end{matrix} \right.\ \Rightarrow \underset{\lbrack - 1;3\rbrack}{\max f(x)} = 20 \Leftrightarrow x = 3$

Vậy đáp án cần tìm là $20$.

b. Ta có: $y' = 2x - \frac{8}{x^{2}} = \frac{2x^{3} - 8}{x^{2}}$

$\Rightarrow y$ $\Rightarrow y' = 0 \Leftrightarrow \frac{2x^{3} - 8}{x^{2}} = 0 \Leftrightarrow x^{3} = 4 \Leftrightarrow x = \sqrt[3]{4}$

Ta có: $\left| \begin{matrix} f\left( \frac{1}{2} \right) = \frac{65}{4} \\ f(2) = 8 \\ f\left( \sqrt[3]{4} \right) = 6\sqrt[3]{2} \\ \end{matrix} \right.\ \Rightarrow \min_{\left\lbrack \frac{1}{2};\frac{1}{2} \right\rbrack}y = 6\sqrt[3]{2}$ $\left| \begin{matrix} f\left( \frac{1}{2} \right) = \frac{65}{4} \\ f(2) = 8 \\ f\left( \sqrt[3]{4} \right) = 6\sqrt[3]{2} \\ \end{matrix} \right.\ \Rightarrow \min_{\left\lbrack \frac{1}{2};\frac{1}{2} \right\rbrack}y = 6\sqrt[3]{2}$.

c. Tập xác định $D = \left( - \infty;\frac{4}{3} \right\rbrack$ $D = \left( - \infty;\frac{4}{3} \right\rbrack$

Ta có: $y' = \frac{- 3}{2\sqrt{4 - 3x}} < 0;\forall x < \frac{4}{3}$

Trên đoạn $\lbrack 0;1\rbrack$ $\lbrack 0;1\rbrack$ hàm số đã cho nghịch biến

$\Rightarrow \min_{\lbrack 0;1\rbrack}y = y(1) = 1$ $\Rightarrow \min_{\lbrack 0;1\rbrack}y = y(1) = 1$

d. Ta có: $y' = 3x^{2} - 3 = 0 \Leftrightarrow \left\lbrack \begin{matrix} x = 1 \\ x = - 1 \\ \end{matrix} \right.$

$\left\{ \begin{matrix} y(1) = - 2 \\ y(2) = 2 \\ \end{matrix} \right.\ \Rightarrow \left\{ \begin{matrix} \max_{\lbrack 1;2\rbrack}y = 2 \\ \min_{\lbrack 1;2\rbrack}y = - 2 \\ \end{matrix} \right.$ $\left\{ \begin{matrix} y(1) = - 2 \\ y(2) = 2 \\ \end{matrix} \right.\ \Rightarrow \left\{ \begin{matrix} \max_{\lbrack 1;2\rbrack}y = 2 \\ \min_{\lbrack 1;2\rbrack}y = - 2 \\ \end{matrix} \right.$

Vậy tổng giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên đoạn $\lbrack 1;2\rbrack$ $\lbrack 1;2\rbrack$ bằng $0$.

Ví dụ: Gọi giá trị lớn nhất và giá trị nhỏ nhất của hàm số $y = f(x) = x + \sqrt{4 - x^{2}}$ $y = f(x) = x + \sqrt{4 - x^{2}}$ lần lượt là $M;m$. Tính giá trị biểu thức $P = M^{2} - m^{2}$ $P = M^{2} - m^{2}$?

Hướng dẫn giải

Tập xác định $D = \lbrack - 2;2\rbrack$ $D = \lbrack - 2;2\rbrack$

Ta có: $y' = 1 - \frac{x}{\sqrt{4 - x^{2}}} \Rightarrow y' = 0 \Leftrightarrow 1 - \frac{x}{\sqrt{4 - x^{2}}} = 0$

$\Leftrightarrow x = \sqrt{4 - x^{2}} \Leftrightarrow \left\{ \begin{matrix} x \geq 0 \\ x^{2} = 4 - x^{2} \\ \end{matrix} \right.\ \Leftrightarrow \left\{ \begin{matrix} x \geq 0 \\ x = \pm \sqrt{2} \\ \end{matrix} \right.\ \Leftrightarrow x = \sqrt{2}$ $\Leftrightarrow x = \sqrt{4 - x^{2}} \Leftrightarrow \left\{ \begin{matrix} x \geq 0 \\ x^{2} = 4 - x^{2} \\ \end{matrix} \right.\ \Leftrightarrow \left\{ \begin{matrix} x \geq 0 \\ x = \pm \sqrt{2} \\ \end{matrix} \right.\ \Leftrightarrow x = \sqrt{2}$

Khi đó: $\left\{ \begin{matrix} f(2) = 2;f( - 2) = - 2 \\ f\left( \sqrt{2} \right) = 2\sqrt{2} \\ \end{matrix} \right.\ \Rightarrow \left\{ \begin{matrix} \max_{\lbrack - 2;2\rbrack}f(x) = M = 2\sqrt{2} \\ \min_{\lbrack - 2;2\rbrack}f(x) = m = - 2 \\ \end{matrix} \right.$ $\left\{ \begin{matrix} f(2) = 2;f( - 2) = - 2 \\ f\left( \sqrt{2} \right) = 2\sqrt{2} \\ \end{matrix} \right.\ \Rightarrow \left\{ \begin{matrix} \max_{\lbrack - 2;2\rbrack}f(x) = M = 2\sqrt{2} \\ \min_{\lbrack - 2;2\rbrack}f(x) = m = - 2 \\ \end{matrix} \right.$

$\Rightarrow P = M^{2} - m^{2} = 4$ $\Rightarrow P = M^{2} - m^{2} = 4$

Ví dụ: Gọi $M;m$ lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số $y = f(x) = \frac{2x - 1}{x + 2}$ $y = f(x) = \frac{2x - 1}{x + 2}$ trên đoạn $\lbrack 0;2\rbrack$ $\lbrack 0;2\rbrack$. Tìm giá trị biểu thức $T = 2m + 4M$?

Hướng dẫn giải

Ta có: $y' = \frac{5}{(x + 2)^{2}} > 0;\forall x \neq - 2$ nên hàm số đồng biến trên $\lbrack 0;2\rbrack$ $\lbrack 0;2\rbrack$

$\Rightarrow \left\{ \begin{matrix} \max_{\lbrack 0;2\rbrack}y = f(2) = \frac{3}{4} \\ \min_{\lbrack 0;2\rbrack}y = f(0) = - \frac{1}{2} \\ \end{matrix} \right.\ \Rightarrow T = 2m + 4M = 2$ $\Rightarrow \left\{ \begin{matrix} \max_{\lbrack 0;2\rbrack}y = f(2) = \frac{3}{4} \\ \min_{\lbrack 0;2\rbrack}y = f(0) = - \frac{1}{2} \\ \end{matrix} \right.\ \Rightarrow T = 2m + 4M = 2$.

Ví dụ: a. Tìm điều kiện tham số m để hàm số $y = f(x) = \frac{x + m}{x + 1}$ $y = f(x) = \frac{x + m}{x + 1}$ thỏa mãn $\max_{\lbrack 1;2\rbrack}y + \min_{\lbrack 1;2\rbrack}y = \frac{9}{2}$ $\max_{\lbrack 1;2\rbrack}y + \min_{\lbrack 1;2\rbrack}y = \frac{9}{2}$?

b. Cho hàm số $y = \frac{x + m}{x - 1}$ $y = \frac{x + m}{x - 1}$ . Định m để hàm số đã cho thỏa mãn $\min_{\lbrack 2;4\rbrack}y = 3$ $\min_{\lbrack 2;4\rbrack}y = 3$?

Hướng dẫn giải

a. Tập xác định $D\mathbb{= R}\backslash\left\{ - 1 \right\}$ $D\mathbb{= R}\backslash\left\{ - 1 \right\}$

Hàm số đơn điệu trên đoạn $\lbrack 1;2\rbrack$ $\lbrack 1;2\rbrack$ nên $\max_{\lbrack 1;2\rbrack}y + \min_{\lbrack 1;2\rbrack}y = f(1) + f(2)$ $\max_{\lbrack 1;2\rbrack}y + \min_{\lbrack 1;2\rbrack}y = f(1) + f(2)$

$\Leftrightarrow \frac{1 + m}{2} + \frac{2 + m}{3} = \frac{9}{2} \Leftrightarrow m = 4$ $\Leftrightarrow \frac{1 + m}{2} + \frac{2 + m}{3} = \frac{9}{2} \Leftrightarrow m = 4$

Vậy đáp án cần tìm là $2 < m \leq 4$ $2 < m \leq 4$.

b. Tập xác định $D\mathbb{= R}\backslash\left\{ 1 \right\}$ $D\mathbb{= R}\backslash\left\{ 1 \right\}$

Ta có: $y' = \frac{- 1 - m}{(x - 1)^{2}}$. Vì hàm số đơn điệu trên $\lbrack 2;4\rbrack$ $\lbrack 2;4\rbrack$ nên

$\left\lbrack \begin{matrix} \min_{\lbrack 2;4\rbrack}y = y(2); - 1 - m > 0 \\ \min_{\lbrack 2;4\rbrack}y = y(4); - 1 - m < 0 \\ \end{matrix} \right.\ \overset{\min_{\lbrack 2;4\rbrack}y = 3}{\rightarrow}\left\lbrack \begin{matrix} 3 = 2 + m;m < - 1 \\ 3 = \frac{4 + m}{3};m > - 1 \\ \end{matrix} \right.$ $\left\lbrack \begin{matrix} \min_{\lbrack 2;4\rbrack}y = y(2); - 1 - m > 0 \\ \min_{\lbrack 2;4\rbrack}y = y(4); - 1 - m < 0 \\ \end{matrix} \right.\ \overset{\min_{\lbrack 2;4\rbrack}y = 3}{\rightarrow}\left\lbrack \begin{matrix} 3 = 2 + m;m < - 1 \\ 3 = \frac{4 + m}{3};m > - 1 \\ \end{matrix} \right.$

$\Leftrightarrow \left\lbrack \begin{matrix} m = 1;m < - 1 \\ m = 5;m > - 1 \\ \end{matrix} \right.\ \Leftrightarrow m = 5$ $\Leftrightarrow \left\lbrack \begin{matrix} m = 1;m < - 1 \\ m = 5;m > - 1 \\ \end{matrix} \right.\ \Leftrightarrow m = 5$

Nếu $m = - 1 \rightarrow y = 1$ $m = - 1 \rightarrow y = 1$ Hàm số không có giá trị lớn nhất

Vậy $m > 4$

Ví dụ: Tính giá trị của tham số m biết rằng giá trị lớn nhất của hàm số $y = x + \sqrt{4 - x^{2}} + m$ $y = x + \sqrt{4 - x^{2}} + m$ là $3\sqrt{2}$ $3\sqrt{2}$?

Hướng dẫn giải

Ta có: $y = x + \sqrt{4 - x^{2}} + m$ $y = x + \sqrt{4 - x^{2}} + m$ có tập xác định $D = \lbrack - 2;2\rbrack$ $D = \lbrack - 2;2\rbrack$

$y' = 1 + \frac{- x}{\sqrt{4 - x^{2}}};\forall x \in ( - 2;2)$

$y' = 0 \Leftrightarrow 1 + \frac{- x}{\sqrt{4 - x^{2}}} = 0 \Leftrightarrow \sqrt{4 - x^{2}} = x$

$\Leftrightarrow \left\{ \begin{matrix} x \geq 0 \\ 4 - x^{2} = x^{2} \\ \end{matrix} \right.\ \Leftrightarrow \left\{ \begin{matrix} x \geq 0 \\ x = \pm \sqrt{2} \\ \end{matrix} \right.\ \Leftrightarrow x = \sqrt{2}$ $\Leftrightarrow \left\{ \begin{matrix} x \geq 0 \\ 4 - x^{2} = x^{2} \\ \end{matrix} \right.\ \Leftrightarrow \left\{ \begin{matrix} x \geq 0 \\ x = \pm \sqrt{2} \\ \end{matrix} \right.\ \Leftrightarrow x = \sqrt{2}$

Ta có: $\left\{ \begin{matrix} y(2) = 2 + m \\ y( - 2) = 2 + m \\ y\left( \sqrt{2} \right) = 2\sqrt{2} + m \\ \end{matrix} \right.$ $\left\{ \begin{matrix} y(2) = 2 + m \\ y( - 2) = 2 + m \\ y\left( \sqrt{2} \right) = 2\sqrt{2} + m \\ \end{matrix} \right.$ .

Theo bài ra ta có: $2\sqrt{2} + m = 3\sqrt{2} \Leftrightarrow m = \sqrt{2}$ $2\sqrt{2} + m = 3\sqrt{2} \Leftrightarrow m = \sqrt{2}$

Vậy đáp án cần tìm là $m = \sqrt{2}$ $m = \sqrt{2}$.

Ví dụ. Cho hàm số $f(x) = x^{3} - 3x^{2} + m^{2} - 2m$ $f(x) = x^{3} - 3x^{2} + m^{2} - 2m$ với $m$ là tham số. Gọi $S$ tập hợp tất cả các giá trị nguyên của tham số $m$ thỏa mãn $3\max_{\lbrack - 3;1\rbrack}f\left( |x| \right) + 2\min_{\lbrack - 3;1\rbrack}f\left( |x| \right) \leq 112$ $3\max_{\lbrack - 3;1\rbrack}f\left( |x| \right) + 2\min_{\lbrack - 3;1\rbrack}f\left( |x| \right) \leq 112$. Tìm số phần tử của tập hợp $S$?

Hướng dẫn giải

Ta có: $f\left( |x| \right) = f\left( | - x| \right);\forall x\mathbb{\in R}$ $f\left( |x| \right) = f\left( | - x| \right);\forall x\mathbb{\in R}$

$\Rightarrow \left\{ \begin{matrix} \max_{\lbrack - 3;1\rbrack}f\left( |x| \right) = \max_{0;3}f(x) \\ \min_{\lbrack - 3;1\rbrack}f\left( |x| \right) = \min_{\lbrack 0;3\rbrack}f(x) \\ \end{matrix} \right.$ $\Rightarrow \left\{ \begin{matrix} \max_{\lbrack - 3;1\rbrack}f\left( |x| \right) = \max_{0;3}f(x) \\ \min_{\lbrack - 3;1\rbrack}f\left( |x| \right) = \min_{\lbrack 0;3\rbrack}f(x) \\ \end{matrix} \right.$

Đạo hàm $f'(x) = 3x^{2} - 6x = 0$

$\Leftrightarrow \left\lbrack \begin{matrix} x = 0 \Rightarrow f(0) = m^{2} - 2m \\ x = 2 \Rightarrow f(2) = m^{2} - 2m - 4 \\ \end{matrix} \right.$ $\Leftrightarrow \left\lbrack \begin{matrix} x = 0 \Rightarrow f(0) = m^{2} - 2m \\ x = 2 \Rightarrow f(2) = m^{2} - 2m - 4 \\ \end{matrix} \right.$ và $f(3) = m^{2} - 2m$ $f(3) = m^{2} - 2m$

Suy ra $3\max_{\lbrack - 3;1\rbrack}f\left( |x| \right) + 2\min_{\lbrack - 3;1\rbrack}f\left( |x| \right) \leq 112$ $3\max_{\lbrack - 3;1\rbrack}f\left( |x| \right) + 2\min_{\lbrack - 3;1\rbrack}f\left( |x| \right) \leq 112$

$\Leftrightarrow 3\left( m^{2} - 2m \right) + 2\left( m^{2} - 2m - 4 \right) \leq 112$ $\Leftrightarrow 3\left( m^{2} - 2m \right) + 2\left( m^{2} - 2m - 4 \right) \leq 112$

$\Leftrightarrow m^{2} - 2m - 24 \leq 0 \Leftrightarrow - 4 \leq m \leq 6$ $\Leftrightarrow m^{2} - 2m - 24 \leq 0 \Leftrightarrow - 4 \leq m \leq 6$

Mà $m\mathbb{\in Z \Rightarrow}m \in \left\{ - 4; - 3;...;5;6 \right\}$ $m\mathbb{\in Z \Rightarrow}m \in \left\{ - 4; - 3;...;5;6 \right\}$

Vậy có tất cả 11 giá trị nguyên của tham số m.

--------------------------------------------------------

Hy vọng rằng nội dung trong bài viết đã giúp bạn hiểu được trình tìm kiếm giá trị lớn nhất – nhỏ nhất của hàm số trên đoạn , bao gồm các hàm xét đạo hàm, kiểm tra điểm tới hạn và so sánh giá trị ở các điểm đầu. Việc thành toán dạng toán này không chỉ giúp bạn làm tốt phần Hàm số trong đề thi THPT Quốc gia mà còn củng cố nền tảng kiến thức kiến thức để giải các dạng bài nâng cao khác trong giải tích.

Hãy lưu lại tài liệu để ôn tập thường xuyên và tiếp tục khám phá thêm nhiều nội dung thuộc Chuyên đề Toán 12 Tìm min max như tìm cực trị hàm số, ứng dụng đạo hàm, bài toán min – max có điều kiện,… Tất cả đều được biên soạn khoa học, dễ hiểu, phù hợp cho học sinh muốn cải thiện điểm số nhanh chóng.

Nếu bạn muốn tổng hợp các dạng bài nâng cao, tạo tệp PDF hoặc viết tiếp các chuyên đề theo yêu cầu, hãy để lại nội dung mong muốn — mình luôn sẵn sàng hỗ trợ bạn!

Gợi ý bài đọc hay:

Tải về

Chọn file muốn tải về: