Giao diện mới của VnDoc Pro: Dễ sử dụng hơn - chỉ tập trung vào lớp bạn quan tâm. Vui lòng chọn lớp mà bạn quan tâm: Lưu và trải nghiệm

Đóng

Điểm danh hàng ngày

Hôm nay +3
Ngày 2 +3
Ngày 3 +3
Ngày 4 +3
Ngày 5 +3
Ngày 6 +3
Ngày 7 +5

Bạn đã điểm danh Hôm nay và nhận 3 điểm! Đăng nhập ngay để nhận điểm

Nhắn tin Zalo VNDOC để nhận tư vấn mua gói Thành viên hoặc tải tài liệu Hotline hỗ trợ: 0936 120 169

VnDoc.com

Sự tương giao và tiếp xúc của mặt cầu với mặt phẳng, đường thẳng

Chuyên đề Toán 12 ôn thi THPT Quốc gia

Bài trước

Tải về

Bài sau

Lớp: Lớp 12

Môn: Toán

Dạng tài liệu: Chuyên đề

Loại File: Word + PDF

Phân loại: Tài liệu Tính phí

Chuyên đề Mặt cầu Toán lớp 12

A. Các kiến thức cần nhớ về sự tương giao, sự tiếp xúc mặt cầu
B. Bài tập tương giao, tiếp xúc của mặt cầu với mặt phẳng, đường thẳng tong không gian

Trong chương trình Toán 12, chuyên đề sự tương giao và tiếp xúc của mặt cầu với mặt phẳng, đường thẳng là một nội dung quan trọng trong hình học không gian. Việc nắm vững kiến thức về quan hệ giữa mặt cầu với các đối tượng hình học khác không chỉ giúp học sinh giải quyết tốt các bài toán trắc nghiệm mà còn vận dụng hiệu quả trong các bài tập vận dụng cao. Bài viết dưới đây sẽ giúp bạn hiểu rõ lý thuyết, công thức áp dụng, cách nhận diện các dạng bài và phương pháp giải nhanh, chính xác.

A. Các kiến thức cần nhớ về sự tương giao, sự tiếp xúc mặt cầu

Các điều kiện tiếp xúc:

+ Đường thẳng $\Delta$ $\Delta$là tiếp tuyến của (S) $\Leftrightarrow$ $\Leftrightarrow$ $\ d(I;\Delta) = R.$ $\ d(I;\Delta) = R.$

+ Mặt phẳng $(\alpha)$ $(\alpha)$là tiếp diện của (S) $\Leftrightarrow$ $\Leftrightarrow$ $\ d\left( I;(\alpha) \right) = R.$ $\ d\left( I;(\alpha) \right) = R.$

Lưu ý các dạng toán liên quan như tìm tiếp điểm, tương giao.

B. Bài tập tương giao, tiếp xúc của mặt cầu với mặt phẳng, đường thẳng tong không gian

Bài tập 1: Cho đường thẳng $(\Delta):\frac{x}{2} = \frac{y - 1}{1} = \frac{z - 2}{- 1}$ $(\Delta):\frac{x}{2} = \frac{y - 1}{1} = \frac{z - 2}{- 1}$ và mặt cầu $(S)$: $x^{2} + y^{2} + z^{2} - 2x + 4z + 1 = 0$ $x^{2} + y^{2} + z^{2} - 2x + 4z + 1 = 0$. Tìm số điểm chung của $(\Delta)$ $(\Delta)$ và $(S)$ ?

Hướng dẫn giải

Đường thẳng $(\Delta)$ $(\Delta)$đi qua $M(0;\ 1;\ 2)$ $M(0;\ 1;\ 2)$ và có một vectơ chỉ phương là $\overrightarrow{u} = (2;\ 1;\ - 1)$ $\overrightarrow{u} = (2;\ 1;\ - 1)$

Mặt cầu $(S)$có tâm $I(1;\ 0;\ - 2)$ $I(1;\ 0;\ - 2)$ và bán kính $R = 2.$

Ta có $\overrightarrow{MI} = (1; - 1; - 4)$ $\overrightarrow{MI} = (1; - 1; - 4)$và $\left\lbrack \overrightarrow{u},\overrightarrow{MI} \right\rbrack = ( - 5;7; - 3)$ $\left\lbrack \overrightarrow{u},\overrightarrow{MI} \right\rbrack = ( - 5;7; - 3)$

$\Rightarrow d(I,\ \Delta) = \frac{\left| \left\lbrack \overrightarrow{u},\overrightarrow{MI} \right\rbrack \right|}{\left| \overrightarrow{u} \right|} = \frac{\sqrt{498}}{6}$ $\Rightarrow d(I,\ \Delta) = \frac{\left| \left\lbrack \overrightarrow{u},\overrightarrow{MI} \right\rbrack \right|}{\left| \overrightarrow{u} \right|} = \frac{\sqrt{498}}{6}$

Vì $d(I,\ \Delta) > R$ $d(I,\ \Delta) > R$ nên $(\Delta)$ $(\Delta)$ không cắt mặt cầu $(S).$

Bài tập 2: Cho điểm $I(1; - 2;3)$. Phương trình mặt cầu tâm I và tiếp xúc với trục Oy là:

A. $(x - 1)^{2} + (y + 2)^{2}(z - 3)^{2} = \sqrt{10}.$ $(x - 1)^{2} + (y + 2)^{2}(z - 3)^{2} = \sqrt{10}.$ B. $(x - 1)^{2} + (y + 2)^{2}(z - 3)^{2} = 10.$ $(x - 1)^{2} + (y + 2)^{2}(z - 3)^{2} = 10.$

C. $(x + 1)^{2} + (y - 2)^{2}(z + 3)^{2} = 10.$ $(x + 1)^{2} + (y - 2)^{2}(z + 3)^{2} = 10.$ D. $(x - 1)^{2} + (y + 2)^{2}(z - 3)^{2} = 9.$ $(x - 1)^{2} + (y + 2)^{2}(z - 3)^{2} = 9.$

Hướng dẫn giải

Gọi M là hình chiếu của $I(1; - 2;3)$ lên Oy, ta có: $M(0; - 2;0)$.

$\overrightarrow{IM} = ( - 1;0; - 3) \Rightarrow R = d(I,Oy) = IM = \sqrt{10}$ $\overrightarrow{IM} = ( - 1;0; - 3) \Rightarrow R = d(I,Oy) = IM = \sqrt{10}$ là bán kính mặt cầu cần tìm.

Phương trình mặt cầu là: $(x - 1)^{2} + (y + 2)^{2}(z - 3)^{2} = 10.$ $(x - 1)^{2} + (y + 2)^{2}(z - 3)^{2} = 10.$

Bài tập 3: Cho điểm $I(1;-2;3)$và đường thẳng d có phương trình $\frac{x + 1}{2} = \frac{y - 2}{1} = \frac{z + 3}{- 1}$ $\frac{x + 1}{2} = \frac{y - 2}{1} = \frac{z + 3}{- 1}$. Viết phương trình mặt cầu tâm I, tiếp xúc với d ?

Hướng dẫn giải

Đường thẳng $(d)$ đi qua $I( - 1;2; - 3)$và có VTCP $\overrightarrow{u} = (2;\ 1;\ - 1) \Rightarrow d(A,\ d) = \frac{\left| \left\lbrack \overrightarrow{u},\overrightarrow{AM} \right\rbrack \right|}{\left| \overrightarrow{u} \right|} = 5\sqrt{2}\$ $\overrightarrow{u} = (2;\ 1;\ - 1) \Rightarrow d(A,\ d) = \frac{\left| \left\lbrack \overrightarrow{u},\overrightarrow{AM} \right\rbrack \right|}{\left| \overrightarrow{u} \right|} = 5\sqrt{2}\$

Phương trình mặt cầu là: $(x - 1)^{2} + (y + 2)^{2}(z - 3)^{2} = 50.$ $(x - 1)^{2} + (y + 2)^{2}(z - 3)^{2} = 50.$

Bài tập 4: Xác định phương trình mặt cầu $(S)$ tâm $I(2;3; - 1)$ cắt đường thẳng $d:\frac{x - 11}{2} = \frac{y}{1} = \frac{z + 25}{- 2}$ $d:\frac{x - 11}{2} = \frac{y}{1} = \frac{z + 25}{- 2}$ tại 2 điểm A, B sao cho $AB = 16$?

Hướng dẫn giải

Hình vẽ minh họa

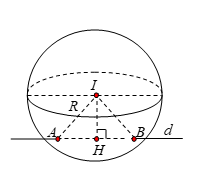
Đường thẳng $(d)$ đi qua $M(11;\ 0; - 25)$ $M(11;\ 0; - 25)$và có vectơ chỉ phương $\overrightarrow{u} = (2;\ 1;\ - 2)$ $\overrightarrow{u} = (2;\ 1;\ - 2)$.Gọi H là hình chiếu của I trên (d). Ta có: $IH = d(I,\ AB) = \frac{\left| \left\lbrack \overrightarrow{u},\overrightarrow{MI} \right\rbrack \right|}{\left| \overrightarrow{u} \right|} = 15$ $IH = d(I,\ AB) = \frac{\left| \left\lbrack \overrightarrow{u},\overrightarrow{MI} \right\rbrack \right|}{\left| \overrightarrow{u} \right|} = 15$

$\Rightarrow R =\sqrt{IH^{2} + \left( \frac{AB}{2} \right)^{2}} = 17$ $\Rightarrow R =\sqrt{IH^{2} + \left( \frac{AB}{2} \right)^{2}} = 17$

Vậy $(S)$ : $(x - 2)^{2} + (y - 3)^{2} + (z + 1)^{2} = 289.$ $(x - 2)^{2} + (y - 3)^{2} + (z + 1)^{2} = 289.$

Bài tập 5: Cho đường thẳng $d:\frac{x + 5}{2} = \frac{y - 7}{- 2} = \frac{z}{1}$ $d:\frac{x + 5}{2} = \frac{y - 7}{- 2} = \frac{z}{1}$ và điểm $I(4;1;6)$. Đường thẳng d cắt mặt cầu $(S)$có tâm I, tại hai điểm A, B sao cho $AB = 6$. Phương trình của mặt cầu $(S)$ là:

A. $(x - 4)^{2} + (y - 1)^{2} + (z - 6)^{2} = 18.$ $(x - 4)^{2} + (y - 1)^{2} + (z - 6)^{2} = 18.$ B. $(x + 4)^{2} + (y +1)^{2} + (z + 6)^{2} = 18.$ $(x + 4)^{2} + (y +1)^{2} + (z + 6)^{2} = 18.$

C. $(x - 4)^{2} + (y - 1)^{2} + (z - 6)^{2} = 9.$ $(x - 4)^{2} + (y - 1)^{2} + (z - 6)^{2} = 9.$ D. $(x - 4)^{2} + (y - 1)^{2} + (z - 6)^{2} = 16.$ $(x - 4)^{2} + (y - 1)^{2} + (z - 6)^{2} = 16.$

Hướng dẫn giải

Hình vẽ minh họa

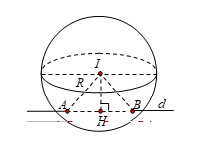
Đường thẳng $d$ đi qua $M( - 5;7;0)$ và có vectơ chỉ phương $\overrightarrow{u} = (2; - 2;1)$ $\overrightarrow{u} = (2; - 2;1)$.

Gọi H là hình chiếu của I trên (d).

Ta có : $IH = d(I,\ AB) = \frac{\left| \left\lbrack \overrightarrow{u},\overrightarrow{MI} \right\rbrack \right|}{\left| \overrightarrow{u} \right|} = 3$ $IH = d(I,\ AB) = \frac{\left| \left\lbrack \overrightarrow{u},\overrightarrow{MI} \right\rbrack \right|}{\left| \overrightarrow{u} \right|} = 3$

$\Rightarrow R = \sqrt{IH^{2} + \left( \frac{AB}{2} \right)^{2}} = 18$ $\Rightarrow R = \sqrt{IH^{2} + \left( \frac{AB}{2} \right)^{2}} = 18$

Vậy $(S)$: $(x - 4)^{2} + (y - 1)^{2} + (z - 6)^{2} = 18.$ $(x - 4)^{2} + (y - 1)^{2} + (z - 6)^{2} = 18.$

✨ Bài viết chỉ trích dẫn một phần nội dung, mời bạn tải tài liệu đầy đủ để nắm trọn kiến thức.

------------------------------------------

FAQ – Sự Tương Giao Và Tiếp Xúc Của Mặt Cầu Với Mặt Phẳng, Đường Thẳng

1. Thế nào là sự tương giao giữa mặt cầu và mặt phẳng?

Sự tương giao giữa mặt cầu và mặt phẳng là vị trí tương đối khi mặt phẳng cắt mặt cầu. Kết quả giao tuyến có thể là:

Một đường tròn.
Một điểm duy nhất (tiếp xúc).
Không có điểm chung.

Việc xác định phụ thuộc vào khoảng cách từ tâm mặt cầu đến mặt phẳng.

2. Khi nào mặt phẳng tiếp xúc với mặt cầu?

Mặt phẳng được gọi là tiếp xúc với mặt cầu khi khoảng cách từ tâm mặt cầu đến mặt phẳng bằng đúng bán kính của mặt cầu.

Khi đó: $d(I,(P)) = R$ và mặt phẳng chỉ có một điểm chung với mặt cầu, gọi là tiếp điểm.

3. Làm sao xác định mặt phẳng cắt mặt cầu theo một đường tròn?

Nếu khoảng cách từ tâm mặt cầu đến mặt phẳng nhỏ hơn bán kính $d(I,(P)) < R$ thì mặt phẳng cắt mặt cầu theo một đường tròn.

Bán kính đường tròn giao tuyến được xác định bằng công thức hình học không gian.

4. Khi nào mặt phẳng không cắt mặt cầu?

Nếu: $d(I,(P)) > R$ thì mặt phẳng nằm ngoài mặt cầu và không có điểm chung với mặt cầu.

5. Thế nào là tiếp tuyến của mặt cầu?

Tiếp tuyến của mặt cầu là đường thẳng chỉ có một điểm chung duy nhất với mặt cầu. Điểm chung đó được gọi là tiếp điểm.

Tại tiếp điểm, bán kính đi qua tiếp điểm vuông góc với tiếp tuyến.

6. Điều kiện để đường thẳng tiếp xúc với mặt cầu là gì?

Đường thẳng tiếp xúc với mặt cầu khi khoảng cách từ tâm mặt cầu đến đường thẳng bằng bán kính: $d(I,\Delta)=R$ $d(I,\Delta)=R$

Đây là điều kiện thường gặp trong các bài tập Toán 12 có đáp án.

7. Làm sao xác định đường thẳng cắt mặt cầu tại hai điểm phân biệt?

Nếu khoảng cách từ tâm mặt cầu đến đường thẳng nhỏ hơn bán kính: $d(I,\Delta) < R$ $d(I,\Delta) < R$

thì đường thẳng cắt mặt cầu tại hai điểm phân biệt.

8. Đường thẳng và mặt cầu không có điểm chung khi nào?

Khi khoảng cách từ tâm mặt cầu đến đường thẳng lớn hơn bán kính $d(I,\Delta)>R$ $d(I,\Delta)>R$ thì đường thẳng nằm ngoài mặt cầu và không giao với mặt cầu.

-----------------------------------

Hy vọng qua chuyên đề sự tương giao và tiếp xúc của mặt cầu với mặt phẳng, đường thẳng, bạn đã nắm được những kiến thức cốt lõi và kỹ năng cần thiết để giải quyết các dạng bài tập liên quan. Đừng quên luyện tập thêm với các đề thi thử và đề kiểm tra để thành thạo hơn. Chúc bạn học tốt và đạt điểm cao trong kỳ thi THPT Quốc gia!

Tải về

Chọn file muốn tải về: