Đề thi thử THPT Quốc gia môn Toán lần 1 năm 2016 trường THPT Chuyên Vĩnh Phúc

Đề thi thử THPT Quốc gia 2016 môn Toán

Đề thi thử THPT Quốc gia môn Toán lần 1 năm 2016 của trường THPT Chuyên Vĩnh Phúc dưới đây được VnDoc sưu tầm và cung cấp cho bạn đọc. Mới đây, Trường THPT Chuyên Vĩnh Phúc đã tổ chức thi thử THPT Quốc gia 2016 lần 1 cho các học sinh trong trường. Hi vọng tài liệu thi đại học 2016 này giúp các bạn có thể ôn tập, luyện thi đại học môn Toán cũng như chuẩn bị cho kì thi tốt nghiệp tốt nhất. Mời các bạn tải về để tham khảo.

Tuyển tập 20 đề thi thử THPT Quốc gia môn Toán năm 2016

Bộ đề thi thử THPT Quốc gia năm 2016 môn Toán - Số 1

Bộ đề thi thử THPT Quốc gia năm 2016 môn Toán - Số 2

Bộ đề thi thử THPT Quốc gia năm 2016 môn Toán - Số 3

Bộ đề thi thử THPT Quốc gia năm 2016 môn Toán - Số 4

Đề thi thử THPT Quốc gia năm 2016 môn Toán trường THPT Chuyên Vĩnh Phúc (Lần 5)

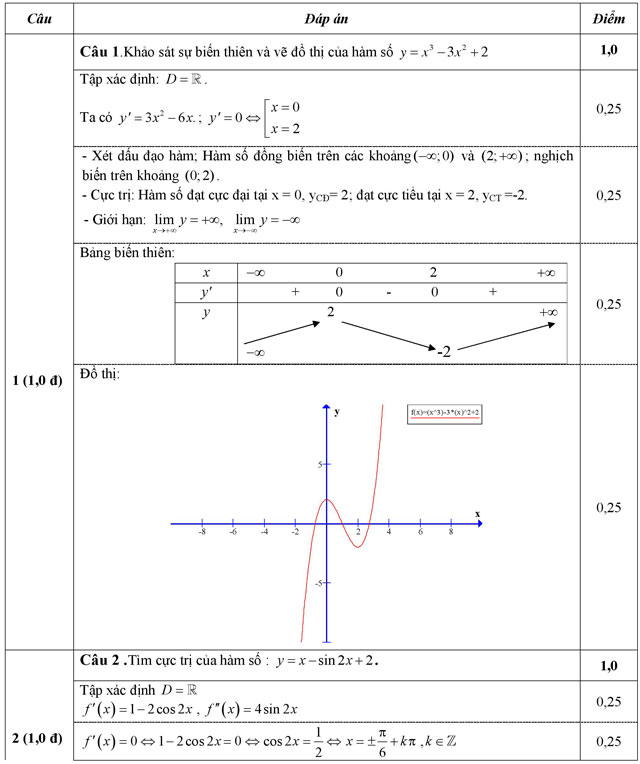
Câu 1 (1,0 điểm). Khảo sát sự biến thiên và vẽ đồ thị của hàm số y = x³ - 3x² + 2.

Câu 2 (1,0 điểm).Tìm cực trị của hàm số: y = x - sin 2x + 2.

Câu 3 (1,0 điểm).

a) Cho tana = 3. Tính giá trị biểu thức

b) Tính giới hạn:

Câu 4 (1,0 điểm). Giải phương trình: 3sin²x – 4sinxcosx + 5 cos²x = 2

Câu 5 (1,0 điểm)

a) Tìm hệ số của x¹⁰ trong khai triển của biểu thức: (3x³ – 2/x²)⁵

b) Một hộp chứa 20 quả cầu giống nhau gồm 12 quả đỏ và 8 quả xanh. Lấy ngẫu nhiên (đồng thời) 3 quả. Tính xác suất để có ít nhất một quả cầu màu xanh.

Câu 6 (1,0 điểm). Trong mặt phẳng với hệ tọa độ (Oxy), cho hình bình hành ABCD có hai đỉnh A(-2;-1), D(5;0) và có tâm I(2;1). Hãy xác định tọa độ hai đỉnh B, C và góc nhọn hợp bởi hai đường chéo của hình bình hành đã cho.

Câu 7 (1,0 điểm)

Cho hình chóp S.ABCD có đáy ABC là tam giác vuông tại A, mặt bên SAB là tam giác đều và nằm trong mặt phẳng vuông góc với mặt phẳng (ABC), gọi M là điểm thuộc cạnh SC sao cho MC = 2MS. Biết AB = 3, BC = 3√3, tính thể tích của khối chóp S.ABC và khoảng cách giữa hai đường thẳng AC và BM.

Câu 8. (1,0 điểm). Trong mặt phẳng với hệ tọa độ (Oxy), cho tam giác ABC ngoại tiếp đường tròn tâm J(2;1). Biết đường cao xuất phát từ đỉnh A của tam giác ABC có phương trình: 2x + y – 10 = 0 và D(2;-4) là giao điểm thứ hai của AJ với đường tròn ngoại tiếp tam giác ABC. Tìm tọa độ các đỉnh tam giác ABC biết B có hoành độ âm và B thuộc đường thẳng có phương trình x + y + 7 = 0.

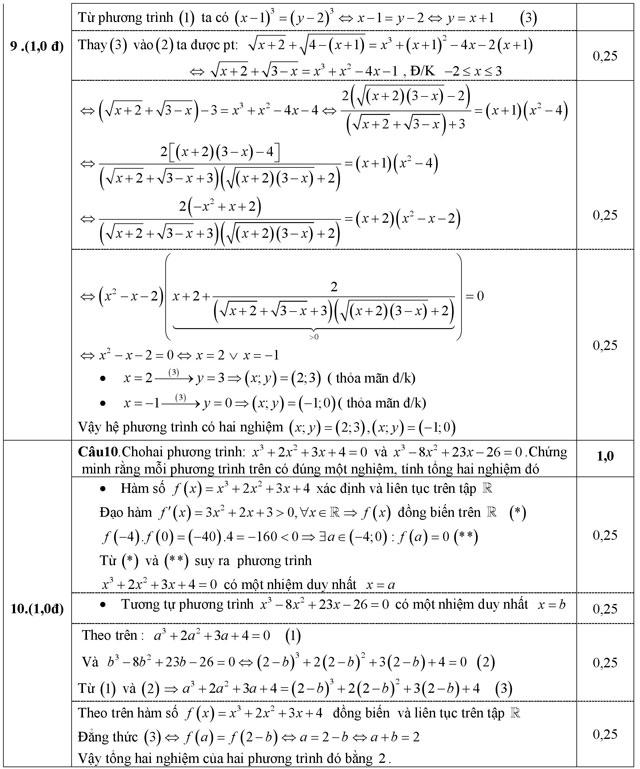
Câu 9 (1,0 điểm). Giải hệ phương trình:

Câu 10 (1,0 điểm). Cho hai phương trình: x³ + 2x² + 3x + 4 = 0 và x³ - 8x² + 23x - 26 = 0. Chứng minh rằng mỗi phương trình trên có đúng một nghiệm, tính tổng hai nghiệm đó.

Đáp án đề thi thử THPT Quốc gia 2016 môn Toán

Đề thi thử THPT Quốc gia môn Toán năm 2016 trường THPT Lý Tự Trọng, Nam Định (Lần 1)

Bộ đề thi thử THPT Quốc gia năm 2016 môn Ngữ văn - Số 1

Bộ đề thi thử THPT Quốc gia năm 2016 môn Sinh học - Số 1

Đề thi thử THPT Quốc gia năm 2016 môn Toán trường THPT Chuyên Đại học Sư phạm Hà Nội (Lần 2)

Đề thi minh họa và đáp án kỳ thi THPT Quốc gia môn Toán

Chú ý: Câu 3b cần sửa lại như sau: = (3 - 1)/[(3 + 3)(3 + √(4.3 - 3))] = 1/18