Đề thi thử THPT Quốc gia năm 2016 môn Toán trường THPT Chuyên Vĩnh Phúc (Lần 5)

Đề thi thử THPT Quốc gia năm 2016 môn Toán

Đề thi thử THPT Quốc gia năm 2016 môn Toán trường THPT Chuyên Vĩnh Phúc (Lần 5) là đề thi thử đại học môn Toán có đáp án dành cho các bạn tham khảo, luyện đề thi thử, chuẩn bị cho kì thi THPT Quốc gia sắp diễn ra rất gần trong tháng 7 tới. Mời các bạn tham khảo.

Đề thi thử THPT Quốc gia môn Toán lần 1 năm 2016 trường THPT Chuyên Vĩnh Phúc

Đề thi thử THPT Quốc gia năm 2016 môn Toán trường THPT Chuyên Vĩnh Phúc (lần 2)

Đề thi thử THPT Quốc gia năm 2016 môn Toán trường THPT Chuyên Vĩnh Phúc (Lần 3)

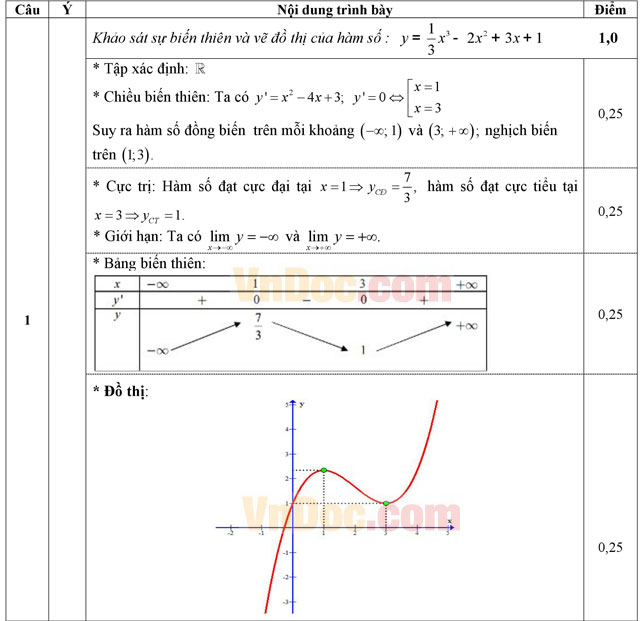
Câu 1 (1,0 điểm). Khảo sát sự biến thiên và vẽ đồ thị của hàm số: .

Câu 2 (1,0 điểm). Tìm miền giá trị của hàm số: .

Câu 3 (1,0 điểm).

a. Cho số phức z thỏa mãn (1 + 2i)z = 5(2 + i)². Tìm phần thực và phần ảo của số phức w = z² + z.

b. Giải phương trình: log₉x(log₃x + 3) = 2.

Câu 4 (1,0 điểm). Tính tích phân sau: .

Câu 5 (1,0 điểm) Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P): 2x - y - 3z + 1 = 0 và điểm I(3; -5; -2). Viết phương trình mặt cầu tâm I và tiếp xúc với mặt phẳng (P). Tìm tọa độ tiếp điểm.

Câu 6 (1,0 điểm).

a) Cho biết tanα = -2; (-π/2 < α < 0. Tính giá trị của biểu thức: A = cosα(2sinα + √3).

b) Một chi đoàn có 15 đoàn viên trong đó có 7 nam và 8 nữ. Người ta chọn ra 4 người trong chi đoàn đó để lập một đội thanh niên tình nguyện. Tính xác suất để trong 4 người được chọn có ít nhất 1 nữ.

Câu 7 (1,0 điểm). Cho hình chóp S.ABCD có đáy ABCD là hình thoi có cạnh bằng a√3; góc BAD = 120^o và cạnh bên SA vuông góc với mặt phẳng đáy. Biết rằng số đo của góc giữa hai mặt phẳng (SBC) và (ABCD) bằng 60^o. Tính theo a thể tích của khối chóp S.ABCD và khoảng cách giữa hai đường thẳng BD và SC.

Câu 8 (1,0 điểm).

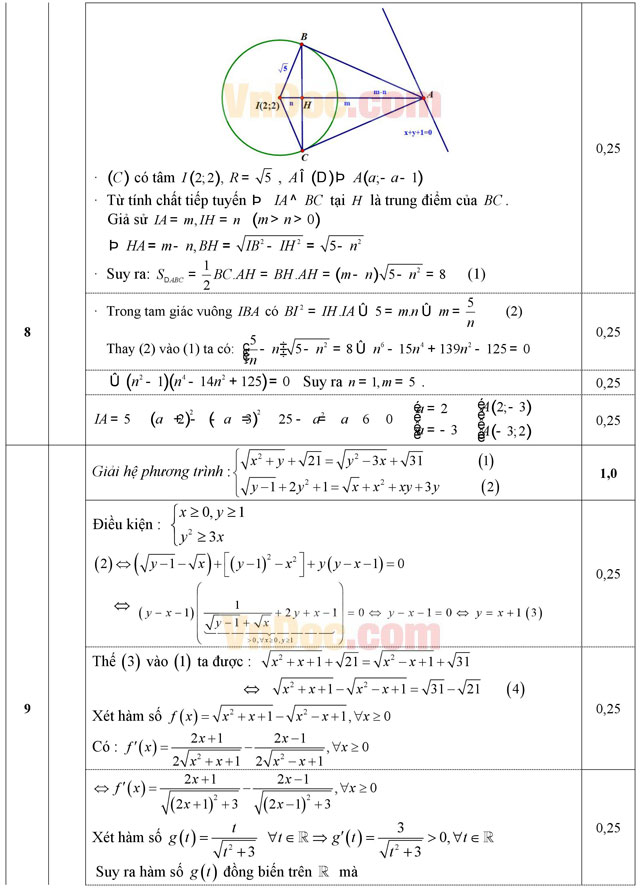
Trong mặt phẳng với hệ tọa độ Oxy, cho đường tròn (C): (x - 2)² + (y - 2)² = 5 và đường thẳng (D): x + y + 1 = 0. Từ điểm A thuộc (D) kẻ hai đường thẳng lần lượt tiếp xúc với (C) tại B và C. Tìm tọa độ điểm A biết rằng diện tích tam giác ABC bằng 8.

Câu 9 (1,0 điểm).

Giải hệ phương trình: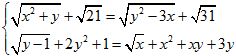

Câu 10 (1,0 điểm).

Cho a, b, c là độ dài của ba cạnh của tam giác ABC có chu vi bằng 3. Tìm giá trị nhỏ nhất của biểu thức: F = 5a² + 5b² + 5c² + 6abc.

Đáp án đề thi thử THPT Quốc gia năm 2016 môn Toán