Đề thi thử THPT Quốc gia môn Toán - Đề 10
Luyện đề thi THPT Quốc gia môn Toán
Để chuẩn bị hiệu quả cho kỳ Thi THPT Quốc gia năm 2025 - 2026, việc luyện tập với các đề thi thử môn Toán có đáp án là bước quan trọng giúp học sinh đánh giá năng lực, rèn kỹ năng xử lý câu hỏi trắc nghiệm và nâng cao tốc độ làm bài. Bài viết này giới thiệu Đề thi thử THPT Quốc gia môn Toán – Đề 10, được biên soạn bám sát cấu trúc đề minh họa, đi kèm đáp án để bạn dễ dàng tự kiểm tra và củng cố kiến thức. Đây là tài liệu cần thiết giúp bạn tăng tốc hiệu quả trong giai đoạn ôn luyện.
ĐỀ THI THỬ THPT QUỐC GIA NĂM 2025 – 2026
ĐỀ ÔN TẬP SỐ 10
THỜI GIAN: 90 PHÚT. NGÀY … /…/2026
PHẦN I. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Câu 1: Cho hàm số 
\(y = f(x)\) xác định trên \(\mathbb{R}\) và có bảng biến thiên như sau:
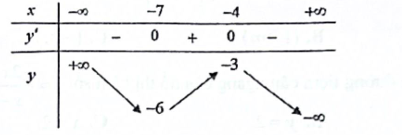
Điểm cực đại của hàm số \(y =
f(x)\) là
A. \(x = - 7\). B. \(x = - 6\). C. \(x = - 3\). D . \(x = - 4\).
Câu 2: Nguyễn hàm \(F(x)\) của hàm số của hàm số \(f(x) = \frac{1}{x} +
e\) là
A. \(F(x) = - \frac{1}{x^{2}} + e^{x} +
C\). B. \(F(x) = \ln|x| + ex +
C\).
C. \(F(x) = \ln|x| + e^{x} + C\) . D. \(F(x) = \ln x + e + C\) .
Câu 3: Một công ty cung cấp nước sạch thống kê lượng nước các hộ gia đình trong một khu vực tiêu thụ trong một tháng ở bảng sau:
Khoảng biến thiên của mẫu số liệu ghép nhóm trên là:
A. \(20m^{3}\). B. \(18m^{3}\). C. \(3m^{3}\) . D. \(15m^{3}\) .
Câu 4: Cho hàm số \(F(x)\) là nguyên hàm của \(f(x)\). Biết \(F(1) = - 3,F( - 2) = 12\). Tính \(I = \int_{- 2}^{1}{f(x)\ }dx\).
A. \(I = 9\). B. \(I = 15\). C. \(I = - 36\) . D. \(I = - 15\) .
Câu 5: Trong không gian \(Oxyz\), mặt phẳng \((P):2x + y - 1 = 0\) có một vectơ pháp tuyến là
A. \({\overrightarrow{n}}_{4} =
(2;1;0)\). B. \({\overrightarrow{n}}_{3} = (1;2;0)\). C. \({\overrightarrow{n}}_{2} = (2;1; -
1)\). D. \({\overrightarrow{n}}_{1} = (
- 2; - 1;1)\).
Câu 6: Cho hình lập phương \(ABCD.A'B'C'D'\). Góc giữa hai vectơ \(\overrightarrow{AB}\) và \(\overrightarrow{CD'}\) bằng:
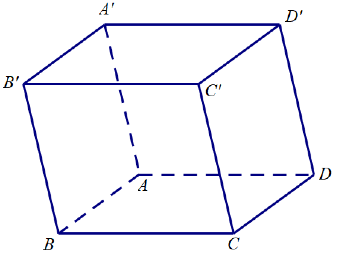
A. \(30{^\circ}\). B. \(135{^\circ}\). C. \(60{^\circ}\). D. \(45{^\circ}\).
Câu 7: Cho hàm số \(y = f(x)\) liên tục trên đoạn \(\lbrack 1;5\rbrack\) và có đồ thị trên như hình vẽ sau. Trên đoạn \(\lbrack 1;5\rbrack\), hàm số đã cho đạt giá trị lớn nhất tại điểm:
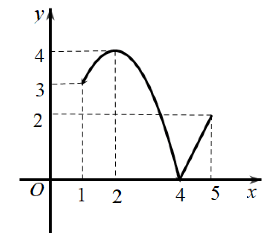
A. \(x = 4\). B. \(x = 1\). C. \(x = 2\). D. \(x = 5\).
Câu 8: Tập nghiệm của bất phương trình \(\log_{\frac{1}{2}}(x + 1) > - 1\) là
A. \(( - 1;1)\). B. \((1; + \infty)\). C. \(( - \infty;1)\). D. \((0;3)\)
Câu 9: Phương trình đường tiệm cận ngang của đồ thị hàm số \(y = \frac{- 2x - 1}{x - 2}\) là
A. \(y = - 2\). B. \(y = 2\). C. \(x =
2\). D. \(x = - 2\).
Câu 10: Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình vuông cạnh \(a\). Cạnh \(SA\) vuông góc với mặt phẳng đáy và có độ dài là \(2a\). Thể tích khối chóp \(S.BCD\) bằng
A. \(\frac{a^{3}}{8}\). B. \(\frac{a^{3}}{3}\). C. \(\frac{a^{3}}{4}\). D. \(\frac{2a^{3}}{3}\).
Câu 11: Cho cấp số nhân \((u_{n})\)với \(u_{1} = 3\) và công bội \(q = - 2\). Giá trị của \(u_{4}\) bằng
A. \(24\). B. \(- 12\). C. \(- 24\). D. \(12\).
Câu 12: Trong không gian \(Oxyz\), cho mặt cầu \((S)\) có phương trình \(x^{2} + y^{2} + z^{2} =
\frac{1}{4}\). Bán kính \(R\) của mặt cầu \((S)\) bằng
A. \(R = \frac{1}{2}\). B. \(R = \frac{1}{4}\). C. \(R = 2\). D. \(R =
4\).
PHẦN II. Câu trắc nghiệm đúng sai.
Câu 13: Khi loại thuốc \(A\) được tiêm vào bệnh nhân, nồng độ (mg/l) của thuốc trong máu sau \(x\) phút (kể từ khi bắt đầu tiêm) được xác định bởi công thức: \(C(x) = \frac{30x}{x^{2}
+ 2}\). (Nguồn: James Stewart, J. (2015). Calculus. Cengage Learning).
a) Thời điểm 1 phút sau khi tiêm, nồng độ thuốc trong máu là 10 (mg/l).
b) Đạo hàm của hàm số \(C(x)\) là \(C'(x) = \frac{60 - 30x^{2}}{(x^{2} +
2)^{2}}\).
c) Trong khoảng thời gian từ 1 phút sau khi tiêm trở đi, nồng độ thuốc trong máu giảm dần.
d) Nồng độ thuốc trong máu đạt giá trị lớn nhất tại thời điểm 2 phút sau khi tiêm.
Câu 14: Trong một hộp đựng \(5\) quả cầu chứa phiếu có thưởng và \(10\) quả cầu chứa phiếu không có thưởng ( các quả cầu cùng hình dạng, kích thước và khối lượng). Hai bạn Bình, An lần lượt lấy ngẫu nhiên ( không hoàn lại ) mỗi bạn một quả. Bạn Bình lấy trước, bạn An lấy sau.
a) Xác suất bạn Bình lấy được quả cầu chứa thưởng là \(\frac{1}{2}\).
b) Biết bạn Bình đã lấy được quả cầu chứa phiếu có thưởng, xác suất để bạn An lấy được quả cầu chứa phiếu có thưởng là \(\frac{2}{7}\).
c) Xác suất để cả hai bạn cùng lấy được quả cầu chứa phiếu có thưởng là \(\frac{2}{21}\).
d) Biết bạn An lấy được quả cầu chứa phiếu có thưởng, xác suất để bạn Bình lấy được quả cầu chứa phiếu có thưởng là \(\frac{2}{7}\).
Câu 15: Trong không gian \(Oxyz\), cho hai điểm \(A(1;2;3),B( -
2;1;1)\)
a) Điểm \(I\left( -
\frac{1}{2};\frac{3}{2};2 \right)\) là trung điểm của đoạn thẳng \(AB\).
b) \(AB = 4\).
c) Phương trình mặt cầu đường kính \(AB\): \(\left( x
+ \frac{1}{2} \right)^{2} + \left( y - \frac{3}{2} \right)^{2} + (z -
2)^{2} = 14\).
d) Xét các điểm \(M\) thuộc mặt phẳng \((Oxz)\) thỏa mãn \(\widehat{AMB} = 90{^\circ}\). Giá trị nhỏ nhất của đoạn \(OM\) không vượt quá \(1\).
Câu 16: Vật thể chuyển động trong 10 phút với vận tốc là giá trị hàm số \(v(t) = \left\{ \begin{matrix}
at^{2} + bt + c\ \ \ \ (0 \leq t \leq 6) \\
m(6 \leq t \leq 10)
\end{matrix} \right.\) (đơn vị: m/phút), phụ thuộc vào thời gian \(t\) (đơn vị: phút). Đồ thị của hàm số vận tốc như hình vẽ sau:
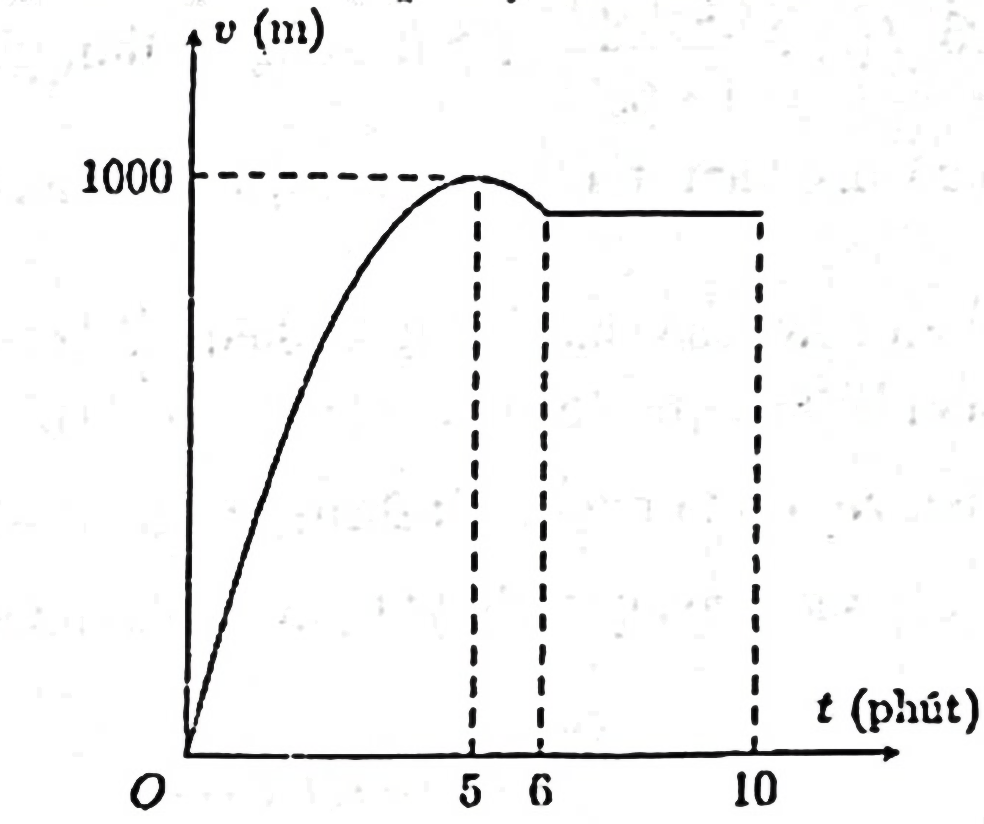
a) Trong khoảng từ phút thứ 6 đến phút thứ 10, vận tốc vật không thay đổi.
b) Quãng đường đi được của vật thể sau 6 phút đầu tiên là \(\int_{0}^{6}{v(t)}dt\)
c) \(5a + b = 20\)
d) Tổng quãng đường đi được của vật thể sau 10 phút đầu tiên là 8160m.
PHẦN III. Câu trắc nghiệm trả lời ngắn.
Câu 1: Cho hình chóp \(SABCD\) có đáy \(ABCD\) là hình chữ nhật, \(AB = 1,AD = \sqrt{3}\). Cạnh bên \(SA\) vuông góc với đáy và \(SA = \frac{\sqrt{3}}{2}\). Số đo góc phẳng nhị diện \(\lbrack S,BD,C\rbrack\) bằng \(a^{0}\). Tìm giá trị \(a\)?
Trả lời:
Câu 2: Người ta làm một sân khấu có hình dạng hai hình tròn giao nhau như hình vẽ. Bán kính hai hình tròn lần lượt là 30 m và 40 m. Khoảng cách giữa tâm hai hình tròn là 50 m.
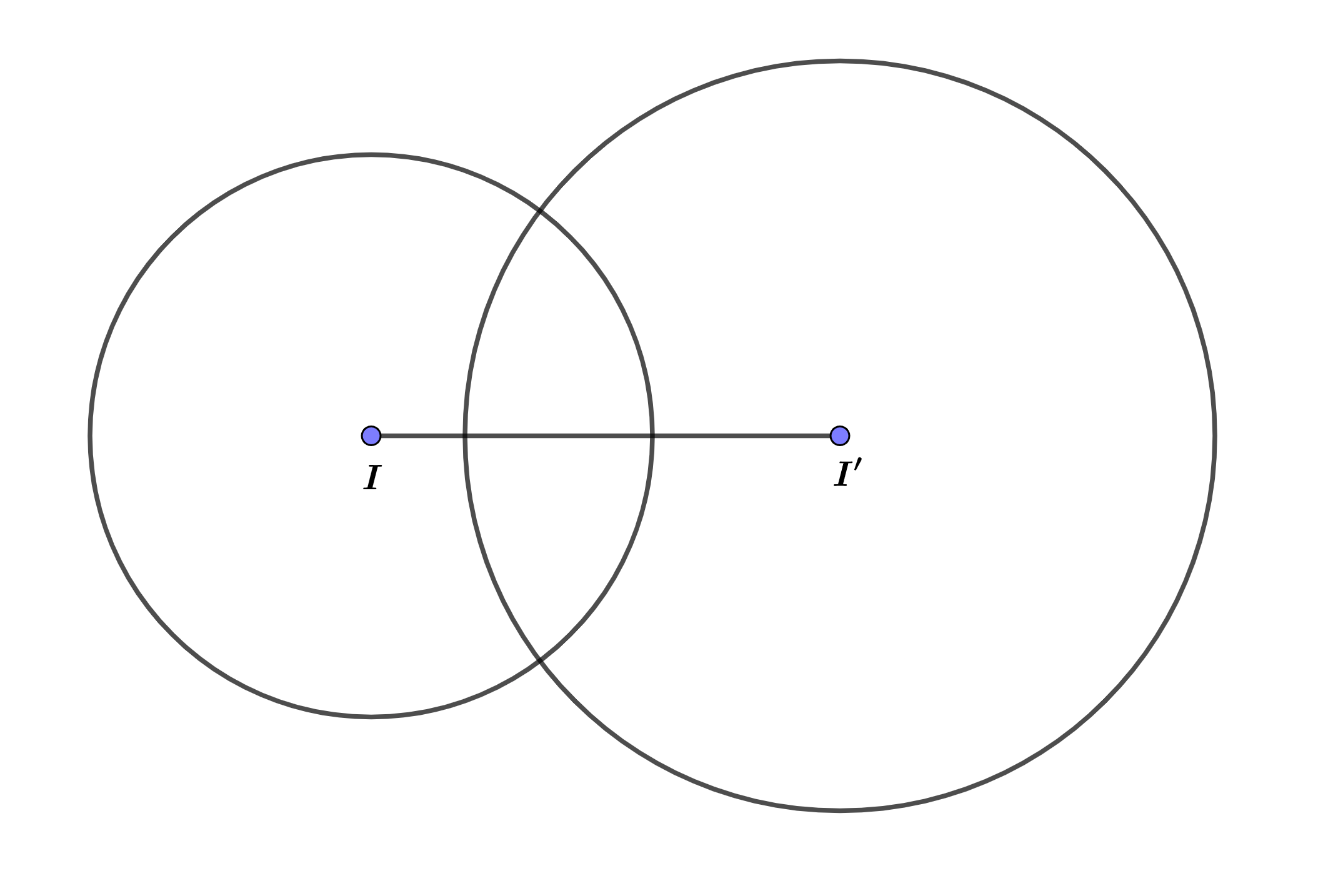
Tính diện tích phần giao nhau của hai hình tròn theo \(m^{2}\) (kết quả làm tròn đến hàng đơn vị).
Trả lời:
Câu 3: Một cơ quan hành chính nhà nước thực hiện việc tinh giản biên chế thông qua phỏng vấn. Tỷ lệ nhân viên của cơ quan thuộc hai nhóm trình độ: Đại học, Cao đẳng lần lượt là \(65\%\) và \(35\%\). Qua phỏng vấn thì tỷ lệ nhân viên bị tinh giản của nhóm đại học là \(10\%\), nhóm cao đẳng là \(15\%\). Chọn một nhân viên bất kỳ đã bị tinh giản thì hãy tính xác suất để người này có trình độ đại học (kết quả là một số thập phân nhỏ hơn 1 đã làm tròn đến hàng phần trăm).
Trả lời:
Câu 4: Trên mỗi cạnh của hình bên dưới, có ghi số phút để đi từ điểm này đến điểm kế tiếp.
Tìm tổng số thời gian ngắn nhất để di chuyển từ điểm \(A\) đến điểm \(D\) trên hình.
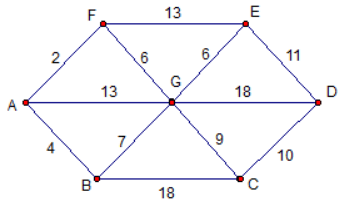
Trả lời:
Câu 5: Doanh số (tính bằng số sản phẩm) của một sản phẩm mới (trong vòng một số năm nhất định) được mô hình hóa bằng hàm số \(f(t) = \frac{24000}{1 + 6e^{- t}},t \geq
0\) trong đó thời gian \(t\) được tính bằng năm, kể từ khi phát hành sản phẩm mới. Khi đó, đạo hàm \(f'(t)\) sẽ biểu thị tốc độ bán hàng. Tốc độ bán hàng lớn nhất đạt được khi \(t = \ln a\). Tìm \(a\).
Trả lời:
Câu 6: Người ta thiết kế một dây cáp chạy thẳng từ điểm \(X\) ở trên mặt đất tới đỉnh \(T\) của một tòa tháp.
Giả sử tọa độ của các điểm là \(T(40;60;150)\) và \(X(100; - 40;0)\) trong hệ tọa độ không gian \(Oxyz,\) với \(O\) là gốc tọa độ đặt tại mặt đất. Người ta muốn nối điểm \(A(40;30; - 20)\) nằm dưới một cái hố tới một điểm \(M(a;b;c)\) nằm trên dây cáp sao khoảng cách \(MA\) này là nhỏ nhất. Tính \(a + b + c.\)
Trả lời:
Toàn bộ nội dung đã sẵn sàng! Nhấn Tải về để tải đầy đủ tài liệu.
