Đề thi thử tốt nghiệp THPT 2025 môn Toán Sở GD&ĐT Đà Nẵng
Thi THPT Quốc gia 2025
Lớp:
THPT Quốc gia
Môn:
Toán
Dạng tài liệu:
Đề thi
Loại:
Tài liệu Lẻ
Loại File:
PDF
Phân loại:
Tài liệu Tính phí
SỞ GIÁO DỤC VÀ ĐÀO TẠO THI THỬ TỐT NGHIỆP TRUNG HỌC PHỔ THÔNG
THÀNH PHỐ ĐÀ NẴNG NĂM HỌC 2024 - 2025
MÔN: TOÁN
ĐỀ CHÍNH THỨC Thời gian làm bài: 90 phút, không kể thời gian giao đề
Đề thi có 22 câu, 04 trang
Thí sinh làm bài trên Phiếu trả lời trắc nghiệm
Họ và tên thí sinh:............................ Số báo danh:................. Phòng thi:................ Mã đề thi: 0126
PHẦN I (3,0 điểm). Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu
12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Câu 1. Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật và SA ⊥ (ABCD). Khoảng cách từ điểm
D đến mặt phẳng (SAB) bằng:
A. SA. B. BD. C. DA. D. SD.
Câu 2. Diện tích hình phẳng giới hạn bởi đồ thị của các hàm số y = sin x, y = cos x và các đường thẳng
x = 0, x = π được tính bằng công thức:
A. S =
π
Z
0
(−sin x + cos x) dx. B. S =
π
Z
0
|sin x − cos x|dx.
C. S =
π
Z
0
(sin x − cos x) dx. D. S =
π
Z
0
(sin x + cos x) dx.
Câu 3. Khảo sát thời gian tự học của một số học sinh lớp 11 trong một ngày, người ta thu được mẫu số
liệu ghép nhóm sau:
Thời gian (phút) [0; 30) [30; 60) [60; 90) [90; 120) [120; 150)
Số học sinh 8 14 11 9 3
Nhóm chứa trung vị của mẫu số liệu trên là:
A. [60; 90). B. [0; 30). C. [30; 60). D. [90; 120).
Câu 4. Trong không gian Oxyz, mặt phẳng (Oyz) có một vectơ pháp tuyến là:
A.
−→
n
3
(1; 1; 1). B.
−→
n
2
(0; 0; 0). C.
−→
n
1
(0; 1; 1). D.
−→
n
4
(1; 0; 0).
Câu 5. Đồ thị hàm số y = −x + 2 +
1
x
có đường tiệm cận xiên là:
A. y = −x + 2. B. y = −
1
x
. C. y = x − 2. D. y =
1
x
.
Câu 6. Tập nghiệm của bất phương trình e
x
> 1 là:
A. (1; +∞). B. (−∞; 0). C. (−∞; +∞). D. (0; +∞).
Câu 7. Nghiệm của phương trình log
4
x = 0 là:
A. x = −1. B. x = 1. C. x = 0. D. x = 4.
Câu 8. Trong không gian Oxyz, phương trình của đường thẳng đi qua điểm E(−1; 4; 2) và điểm F (−5; 0; 3)
là:
A.
x + 1
−4
=
y − 4
−4
=
z − 2
1
. B.
x + 4
−1
=
y + 4
4
=
z − 1
2
.
C.
x − 4
−1
=
y − 4
4
=
z + 1
2
. D.
x − 1
−4
=
y + 4
−4
=
z + 2
1
.
Câu 9. Nguyên hàm của hàm số f(x) = 2 sin x là:
A. −cos x + C. B. cos x + C. C. 2 cos x + C. D. −2 cos x + C.
Câu 10. Cho cấp số cộng (u
n
) có u
1
= 1 và u
2
= −3. Số hạng u
4
của cấp số cộng đã cho là:
A. −11. B. −27. C. −7. D. −14.
Câu 11. Cho hàm số y = x
3
− 3x
2
− 2025. Hàm số đã cho nghịch biến trên khoảng:
A. (0; 2). B. (−∞; 0). C. (−∞; +∞). D. (2; +∞).
1
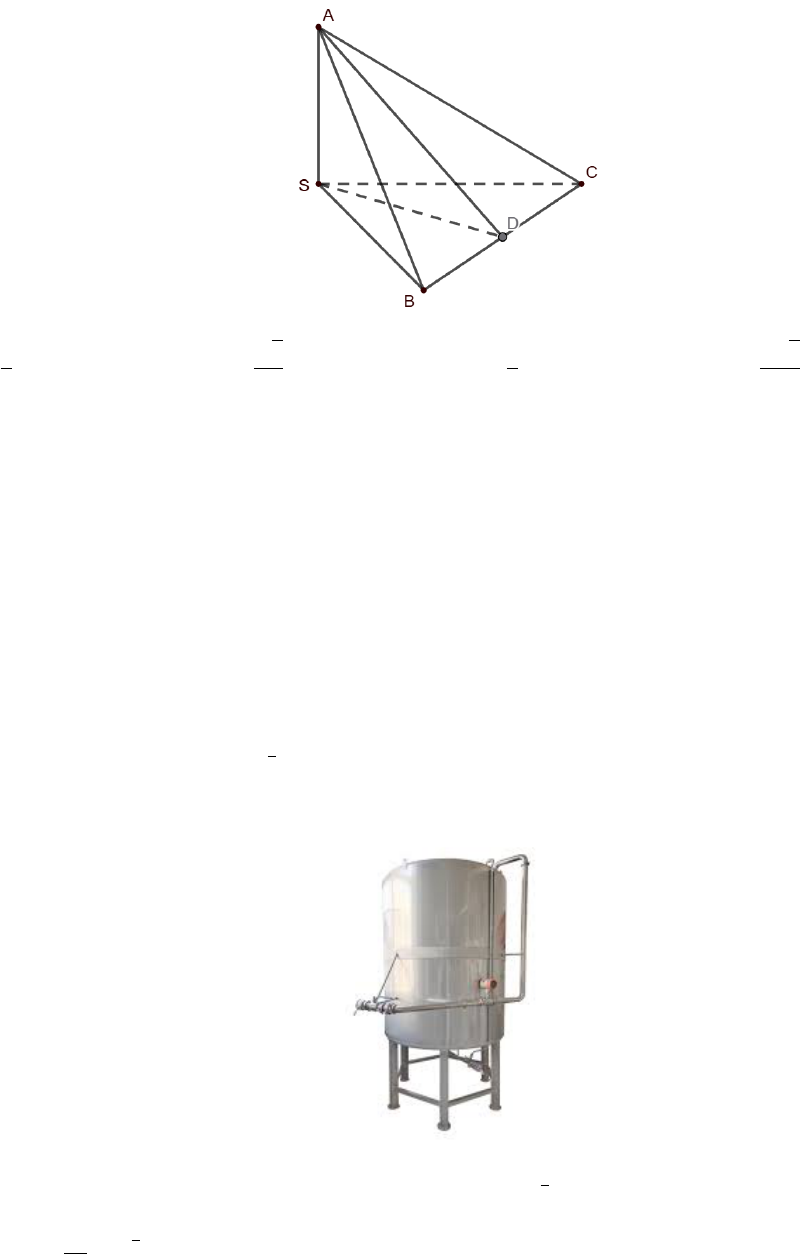
Câu 12. Cho tứ diện S.ABC có các cạnh SA, SB, SC đôi một vuông góc và SA = SB = SC = 1. Gọi α
là góc phẳng nhị diện [S, BC, A]. Tính cos α.
A.
2
5
. B.
√
3
3
. C.
1
3
. D.
2
√
5
5
.
PHẦN II (4,0 điểm). Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 4 . Trong mỗi ý
a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Câu 1. Cho hàm số f(x) = −2x
4
+ 4x
2
+ 1 có đồ thị (C).
a) lim
x→−∞
f(x) = −∞.
b) Đạo hàm của hàm số đã cho là f
′
(x) = −8x
3
+ 8x + 1.
c) Tập nghiệm của phương trình f
′
(x) = 0 là S = {−1; 0; 1}.
d) Giá trị lớn nhất của hàm số f(x) là 1.
Câu 2. Một bể chứa dầu ban đầu có 50.000 lít dầu. Gọi V (t) là thể tích dầu (lít) trong bể tại thời điểm t,
trong đó t tính theo giờ (0 ≤ t ≤ 24). Trong quá trình bơm dầu vào bể, thể tích dầu tăng theo tốc độ được
biểu diễn bởi hàm số V
′
(t) = k ·
√
t, với k là hằng số dương. Sau 4 giờ bơm liên tục, thể tích dầu trong bể
đạt 58.000 lít.
a) Hàm số V (t) là một nguyên hàm của hàm số f(t) = k ·
√
t.
b) V (t) =
2k
3
· t
√
t + C, với 0 ≤ t ≤ 24 và k, C là các hằng số.
c) Sau 16 giờ bơm liên tục, thể tích dầu trong bể đạt được 148.000 lít.
d) Trong quá trình bơm dầu, nếu sau mỗi giờ lượng dầu bị rò rỉ đều đặn với tốc độ 500 lít/giờ, thì tại
thời điểm t = 9 giờ, thể tích dầu trong bể là 72.500 lít.
Câu 3. Một nghiên cứu tại một trường đại học cho biết tỷ lệ sinh viên dùng cà phê để duy trì tinh táo khi
học vào ban đêm là 70%. Giả sử chọn ngẫu nhiên 3 sinh viên từ nhóm khảo sát trên để phỏng vấn.
2

a) Xác suất để cả 3 sinh viên đều dùng cà phê để duy trì tinh táo là 0,343.
b) Xác suất trong 3 sinh viên có ít nhất 1 sinh viên không dùng cà phê là 0,657.
c) Xác suất trong 3 sinh viên có đúng 1 sinh viên dùng cà phê là 0,189.
d) Xác suất trong 3 sinh viên có đúng 2 sinh viên dùng cà phê và 1 sinh viên không dùng cà phê lớn hơn
0,45.
Câu 4. Một radar phòng không được đặt tại vị trí gốc tọa độ O(0; 0; 0) trong không gian Oxyz, mỗi đơn
vị trên các trục tọa độ tương ứng với 1 km. Radar này có khả năng phát hiện các mục tiêu bay trong bán
kính 250 km. Một máy bay không người lái (UAV) đang bay thẳng đều từ vị trí điểm A(300; −400; 100)
đến điểm B(−300; 400; 100). UAV bay với vận tốc không đổi 900 km/h và mang theo thiết bị gây nhiễu
chủ động có tầm hiệu quả 50 km tính từ UAV.(tham khao từ Stimson’s Introduction to Airborne Radar, 3rd
Edition,George W. Stimson, Hugh D. Griffiths, Christopher Baker, Dave Adamy.)
a) Radar không thể phát hiện UAV khi UAV ở vị trí A.
b) Phương trình tham số của đường bay của UAV là
x = 300 − 3t
y = −400 + 4t
z = 100
, t ∈ R.
c) Trong suốt quá trình bay, sẽ có thời điểm UAV gây nhiễu được radar.
d) Radar có thể theo dõi UAV trong khoảng thời gian hơn 30 phút.
PHẦN III (3.0 điểm). Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 6 .
Câu 1. Một chiếc lều hình chóp có đáy là hình vuông, mỗi cạnh dài 200 cm. Đỉnh lều nằm thẳng đứng
phía trên tâm của hình vuông, và chiều cao của lều là 206 cm. Người ta dùng 4 cọc bằng nhau nối từ 4 góc
của đáy đến đỉnh lều để dựng lều. Chiều dài tối thiểu của mỗi cây cọc là bao nhiêu centimet (làm tròn kết
quả đến hàng đơn vị của cm)?
Câu 2. Một giáo viên theo dõi sự tiến bộ của học sinh qua thang đo điểm, được mô hình hóa bằng hàm số
f(x) = x
3
+ ax
2
+ bx + c với a, b, c là các hệ số. Trong đó, x (0 ≤ x ≤ 9, x ∈ N) là số tháng kể từ đầu năm
học và f(x) là điểm trong tháng thứ x. Qua theo dõi, giáo viên ghi nhận tháng đầu tiên học sinh đạt 19
điểm, sau đó giảm trong tháng thứ hai và đến tháng thứ ba học sinh đạt mức điểm thấp nhất trong năm
học, là 3 điểm. Kể từ tháng thứ ba trở đi, điểm của học sinh tăng lên. Tính điểm của học sinh đó ở tháng
thứ sáu.
3
Đề thi thử tốt nghiệp môn Toán Sở Đà Nẵng
Đề thi thử tốt nghiệp THPT Quốc gia 2025 môn Toán Sở GD&ĐT Đà Nẵng có đáp án được VnDoc.com tổng hợp và xin gửi tới bạn đọc cùng tham khảo. Bài viết được tổng hợp gồm có 4 mã đề thi. Đề thi được biên soạn theo cấu trúc đề thi mới. Mỗi đề thi gồm có 12 câu hỏi trắc nghiệm nhiều phương án lựa chọn, 4 câu hỏi trắc nghiệm đúng sai và 6 câu hỏi trắc nghiệm trả lời ngắn. Thí sinh làm bài trong thời gian 90 phút. Đề có đáp án kèm theo. Mời các bạn cùng theo dõi đề thi dưới đây để có thêm tài liệu ôn Thi THPT Quốc gia sắp tới nhé.


