Đề thi thử tốt nghiệp THPT 2025 môn Toán cụm các trường THPT Hải Dương
Thi THPT Quốc gia 2025
Lớp:
THPT Quốc gia
Môn:
Toán
Dạng tài liệu:
Đề thi
Loại:
Tài liệu Lẻ
Loại File:
Word + PDF
Phân loại:
Tài liệu Tính phí
Mã đề 1210_Trang 1/6
ĐỀ CHÍNH THỨC
(Đề có 06 trang)
ĐỀ THI THỬ TỐT NGHIỆP THPT NĂM 2025
MÔN: TOÁN. Lớp 12
Ngày thi: 05-06/4/2025
Thời gian làm bài: 90 phút, không kể thời gian phát đề
Họ tên thí sinh: ……………………………………Số báo danh: ……………..
Mã đề thi 1210
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi
câu hỏi thí sinh chỉ chọn một phương án.
Câu 1. Trong các phương trình sau, phương trình nào vô nghiệm?
A.
tan 99x=
. B.
3
sin 2
4
x =-
.
C.
cot 4x=
. D.
cos 2 2025
2
x
p
æö
÷
ç
-=
÷
ç
÷
ç
èø
.
Câu 2. Trong không gian
,Oxyz
cho điểm
(1;2; 1)A -
và
(1;3;1).AB =
uuur
Tọa độ của điểm
B
là:
A.
( 2; 5;0).--
B.
(0;1;2).
C.
(2;5;0).
D.
(0; 1; 2).--
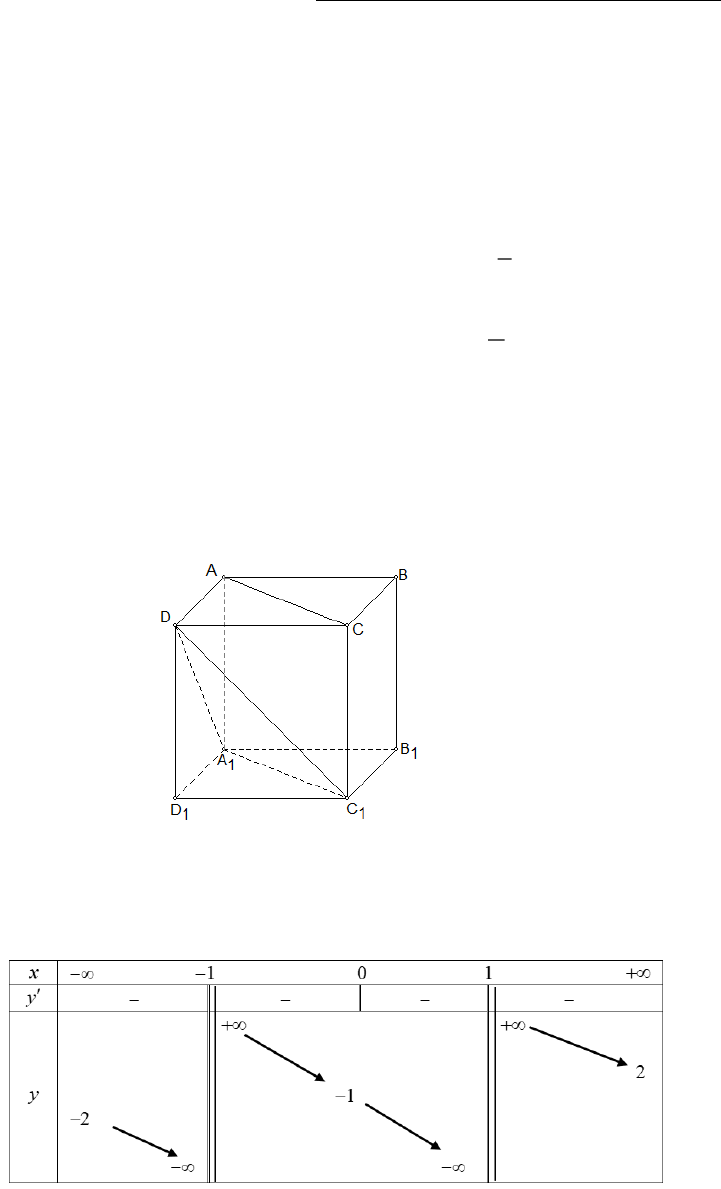
Câu 3. Cho hình lập phương
1 1 1 1
.ABCD A B C D
. Góc giữa
AC
và
1
DA
bằng:
A.
0
90
. B.
0
45
. C.
0
120
. D.
0
60 .
Câu 4. Cho hàm số
()y f x
xác định trên tập
\ 1;1R
, liên tục trên mỗi khoảng xác định và có
bảng biến thiên như sau:
Hỏi đồ thị hàm số có bao nhiêu tiệm cận ngang?
A.
2
B.
0
C.
1
D.
4
Mã đề 1210_Trang 2/6
Câu 5. Cho cấp số cộng
()
n
u
có
1
4; 3ud
. Giá trị của
10
u
bằng:
A.
10
31u
. B.
10
23u
. C.
10
20u
. D.
10
15u
.
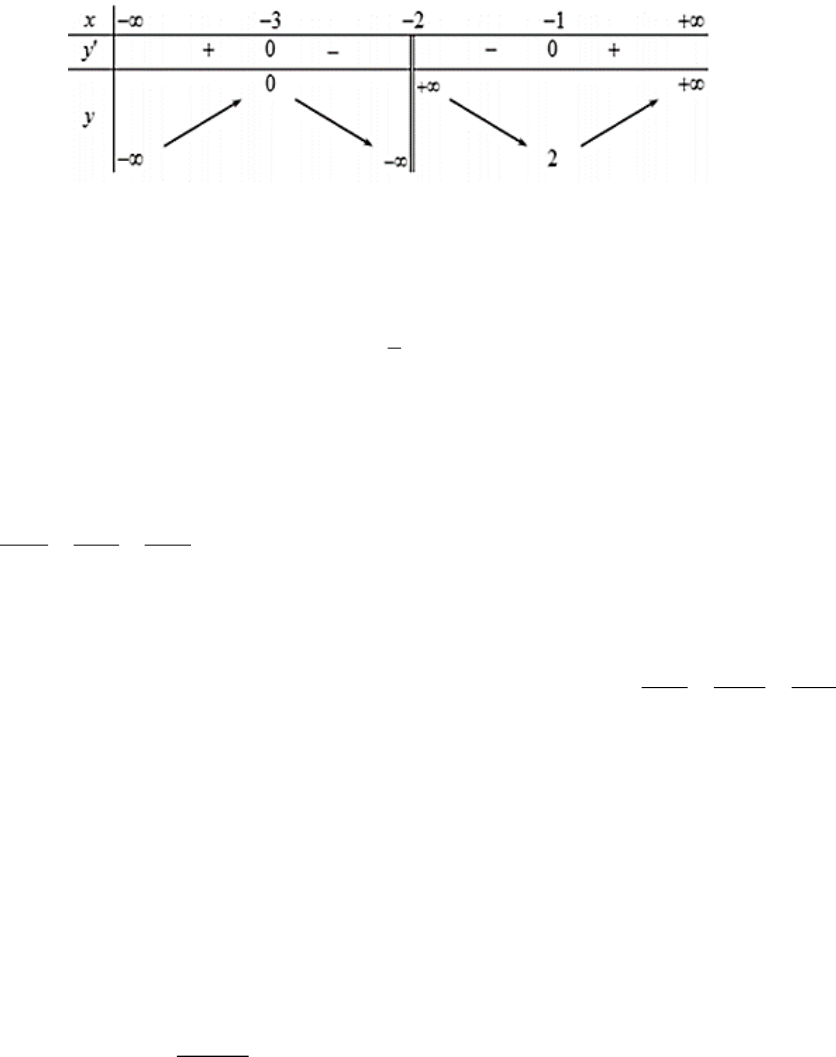
Câu 6. Cho hàm số
y f x
có bảng biến thiên như sau:
Hàm số đã cho nghịch biến trên khoảng nào dưới đây?
A.
3; 1
. B.
2; 1
.
C.
;0
. D.
3; 2 2; 1
.
Câu 7. Tập nghiệm
S
của bất phương trình
1
50
5
x
là:
A.
1;S
. B.
2;S
. C.
1;S
. D.
;2S
.
Câu 8. Trong không gian với hệ tọa độ
Oxyz
, cho mặt phẳng
:6 8 10 1 0P x y z
và đường
thẳng
2 1 5
:
3 4 5
x y z
d
. Góc giữa đường thẳng
d
và mặt phẳng
P
bằng:
A.
90
. B.
45
. C.
60
. D.
30
.
Câu 9. Trong không gian
Oxyz
, điểm nào dưới đây thuộc đường thẳng
1 2 1
:
1 3 3
x y z
d
?
A.
1; 2; 1Q
. B.
1;3;2N
. C.
1;2;1P
. D.
1;2;1A
.
Câu 10. Cho hàm số
fx
có đạo hàm liên tục trên đoạn
1;3
và thỏa mãn
1 2, 3 4ff
.
Tính tích phân
3
1
dI f x x
.
A.
2I
. B.
3I
. C.
1I
. D.
4I
.
Câu 11. Một quần thể virut Corona
P
có P(t) là số lượng virut Corona P sau t giờ,
0t
và đang
thay đổi với tốc độ
5000
1 0,2
Pt
t
, trong đó
t
là thời gian tính bằng giờ. Quần thể virut Corona
P
ban đầu có số lượng là
1000
con. Số lượng virut Corona sau
3
giờ gần với số nào sau đây nhất?
A.
16000
. B.
21750
. C.
12750
. D.
11750
.
Câu 12. Doanh thu bán hàng trong 20 ngày được lựa chọn ngẫu nhiên của một của hàng được
ghi lại ở bảng sau :
Mã đề 1210_Trang 3/6
Tứ phân vị thứ ba của mẫu số liệu gần nhất với giá trị nào trong các giá trị dưới đây?
A.
10
. B.
11
. C.
12
. D.
13
.
PHẦN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d)
ở mỗi câu, thí sinh chọn đúng hoặc sai.
Câu 1. Ở cửa ra vào của nhà sách Nguyễn Văn Cừ có một thiết bị cảnh báo hàng hóa chưa được
thanh toán khi qua cửa. Thiết bị phát chuông cảnh báo với
99%
các hàng hóa ra cửa mà chưa thanh
toán và
0,1%
các hàng hóa đã thanh toán. Tỷ lệ hàng hóa qua cửa không được thanh toán là
0,1%
.
Chọn ngẫu nhiên một hàng hóa khi đi qua cửa. Xét tính đúng sai của các mệnh đề sau?
a) Xác suất để hàng hóa qua cửa đã thanh toán là
0,999
.
b) Xác suất để hàng hóa qua cửa chưa thanh toán và thiết bị phát chuông cảnh báo là
0,01
.
c) Biết rằng hàng hóa qua cửa đã thanh toán, xác suất để thiết bị phát chuông cảnh báo là
0,001
.
d) Xác suất hàng hóa qua cửa chưa thanh toán và thiết bị không phát chuông cảnh báo là
5
10
.
Câu 2. Trong không gian
Oxyz
, cho bốn điểm
1 1 4 2 7 9 0 9 13; ; ; ; ; ; ; ;A B C
;
1 8 10;;D
. Mệnh
đề nào sau đây đúng và mệnh đề nào sai?
a)
65
uuur r r r
.AB i j k
b)
uuur uuur
.AB AC
c) Phương trình mặt phẳng đi qua điểm
B
và vuông góc với
AC
là
8 9 14 0 .x y z
d) Phương trình mặt phẳng chứa
AB
song song với
CD
là
8 7 13 50 0 .x y z
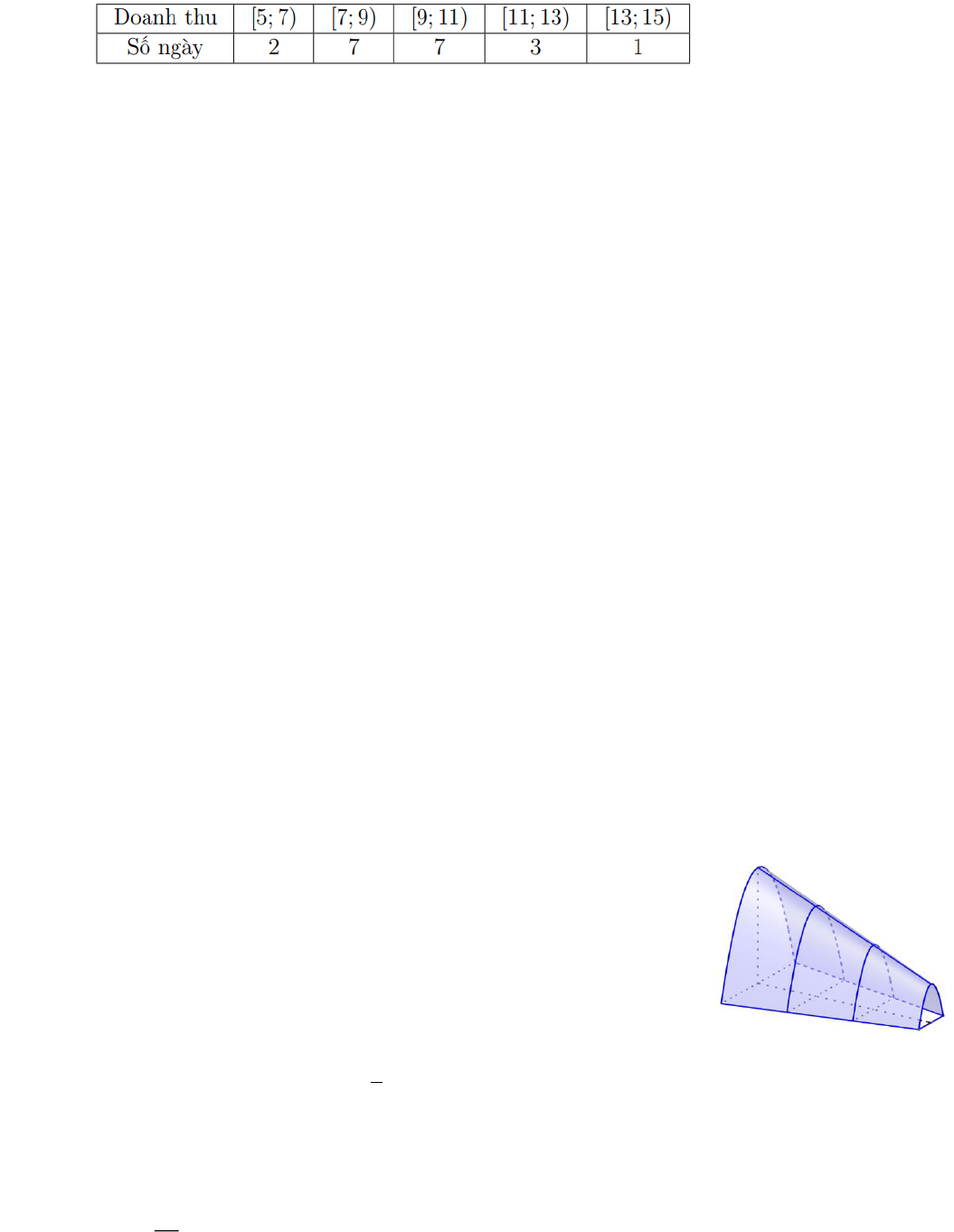
Câu 3. Một đường hầm mô hình như hình vẽ có chiều dài
5
( )
cm
. Khi cắt mô
hình này bởi các mặt phẳng vuông góc với đáy của nó, ta được mặt cắt là một
hình parabol có độ dài đáy gấp đôi chiều cao. Ở đó hình parabol là hình phẳng
được giới hạn bởi một đường parabol và đoạn thẳng nối hai điểm thuộc parabol
đồng thời vuông góc với trục đối xứng của parabol đó được gọi là đáy, khoảng
cách từ đỉnh của parabol xuống đáy gọi là chiều cao. Chiều cao của mỗi mặt cắt
hình parabol cho bởi công thức
2
3
5
yx=-
( )
cm
, với
x
( )
cm
là khoảng cách tính từ lối vào lớn
hơn của đường hầm mô hình đến mặt phẳng chứa mặt cắt.
a) Nếu một hình parabol có đáy bằng
d
và chiều cao bằng
h
như hình vẽ thì phương trình của
parabol là
2
2
4
.
h
y x h
d
= - +
Đề thi thử tốt nghiệp môn Toán cụm trường THPT Hải Dương
Đề thi thử tốt nghiệp THPT Quốc gia 2025 môn Toán cụm các trường THPT Hải Dương có đáp án là tài liệu hữu ích giúp bạn đọc có thể trau dồi nội dung kiến thức, chuẩn bị thật tốt cho kì Thi THPT Quốc gia sắp tới nhé. Bài viết được tổng hợp gồm có 2 mã đề thi. Đề thi được biên soạn theo cấu trúc đề thi mới. Mỗi đề thi gồm có 12 câu hỏi trắc nghiệm nhiều phương án lựa chọn, 4 câu hỏi trắc nghiệm đúng sai và 6 câu hỏi trắc nghiệm trả lời ngắn. Thí sinh làm bài trong thời gian 90 phút. Đề có đáp án kèm theo. Mời các bạn cùng theo dõi đề thi dưới đây.


